文档内容
2023—2024 学年度下学期教学质量监测
高一年级数学试题卷
(考试时间:120分钟;满分:150分)
注意事项:
1.本卷为试题卷,考生必须在答题卡上解题作答,答案书写在答题卡相应位置,在试题卷、
草稿纸上作答无效.选择题作答必须用2B铅笔填涂.
2.考试结束后,请将答题卡交给监考教师.
一、单项选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只
有一个选项是正确的.请把正确的选项填涂在答题卡相应的位置上.
1. 求复数 的模为( )
A. B. C. D. 2
【答案】A
【解析】
【分析】利用复数的除法可得 ,进而即得.
【详解】法一:∵ ,
∴ ;
法二: ,
故选:A.
2. 某样本中共有 个个体,其中四个值分别为 ,第五个值丢失,但该样本的平均数为 ,则样本方
差为( )
第1页/共16页
学科网(北京)股份有限公司A. B. C. D.
【答案】A
【解析】
【分析】利用平均数可求得丢失的数据,根据方差计算公式可求得结果.
【详解】设丢失的数据为 ,则 ,解得: ,
样本方差 .
故选:A.
3. 已知正方形 的边长为 , , ,则 等于( )
A. B. C. D.
【答案】D
【解析】
【分析】结合向量的加法原则即可得 ,然后计算长度即可.
【详解】设AB的中点为E,故 = ,
所以 = + = ,而 ,故 = .
第2页/共16页
学科网(北京)股份有限公司故选:D
4. 已知一组数据5,7,6,3,9,4,8,10,则这组数据的 分位数是( )
A. 3.5 B. 4.5 C. 5 D. 5.5
【答案】B
【解析】
【分析】利用百分位数的求法即可得解.
【详解】将这组数据从小到大排列得, ,共8个数,
又 ,所以这组数据的 分位数为 .
故选:B.
5. 若圆锥、圆柱的底面直径和它们的高都等于一个球的直径,则圆锥、圆柱、球的体积之比为( )
A. B. C. D.
【答案】B
【解析】
【分析】
设球的半径为 ,将三个几何体的体积都用 ,即可得答案.
【详解】设球的半径为 ,
则 , , ,
所以 .
.
故选:B
【点睛】本题考查圆锥、圆柱、球的体积计算,考查运算求解能力,属于基础题.
6. 在 中,若 ,则最大角的余弦值为
A. B. C. D.
【答案】D
【解析】
第3页/共16页
学科网(北京)股份有限公司【 详 解 】 试 题 分 析 : , 所 以 最 大 角 为 C ,
,选D.
考点:余弦定理
7. 若 ,则 等于
A. B.
C. 0 D.
【答案】C
【解析】
详解】 .
【
故选:C.
8. 已知函数f(x)=x(ex+ae﹣x)(x∈R),若函数f(x)是偶函数,记a=m,若函数f(x)为奇函数,记
a=n,则m+2n的值为
A. 0 B. 1 C. 2 D. ﹣1
【答案】B
【解析】
【详解】试题分析:利用函数f(x)=x(ex+ae﹣x)是偶函数,得到g(x)=ex+ae﹣x为奇函数,然后利用g
(0)=0,可以解得m.函数f(x)=x(ex+ae﹣x)是奇函数,所以g(x)=ex+ae﹣x为偶函数,可得n,即可
得出结论.
解:设g(x)=ex+ae﹣x,因为函数f(x)=x(ex+ae﹣x)是偶函数,所以g(x)=ex+ae﹣x为奇函数.
又因为函数f(x)的定义域为R,所以g(0)=0,
即g(0)=1+a=0,解得a=﹣1,所以m=﹣1.
因为函数f(x)=x(ex+ae﹣x)是奇函数,所以g(x)=ex+ae﹣x为偶函数
所以(e﹣x+aex)=ex+ae﹣x即(1﹣a)(e﹣x﹣ex)=0对任意的x都成立
所以a=1,所以n=1,
所以m+2n=1
第4页/共16页
学科网(北京)股份有限公司故选B.
考点:函数奇偶性的性质.
二、多项选择题:本大题共3小题,每小题6分,共18分.在每小题给出的四个选项中,有
多项符合题目要求.全部选对得6分,选对但不全的得部分分,有选错的得0分.
9. 已知向量 ,则下列结论正确 的是( )
A. 在 上的投影向量是
B.
C. 向量 与向量 的夹角为
D.
【答案】BD
【解析】
【分析】先利用向量垂直坐标表示验证选项D,选项B利用平面向量模的公式计算即可,选项C利用向量
夹角的坐标表示求解即可;选项A利用向量坐标求解投影向量即可.
【详解】对于D,因为 ,所以 ,
所以 ,故D正确;
对于B,因为 ,
所以 ,故B正确;
对于C,因为 ,
所以 ,
又 ,则 ,故C错误;
对于A, 在 方向上的投影向量为 ,故A错误.
第5页/共16页
学科网(北京)股份有限公司故选:BD.
10. 已知随机事件A,B满足 , ,则( )
A. 若事件A,B互斥,则
.
B 若 ,则事件A,B互斥
C. 若事件A,B相互独立,则
D. 若 ,则事件A,B相互独立
【答案】ACD
【解析】
【分析】利用互斥事件的定义判断AB,利用相互独立事件的定义判断CD.
【详解】对于A选项, ,故A正确;
对于B选项, , ,A,B互斥,否则不一定有A,B互斥,故B
错误;
对于C选项,因为事件A,B相互独立,故 ,故C正确;
对于D选项,因为 ,故事件A,B相互独立,故D正确.
故选:ACD.
11. 如果若干个函数的图象经过平移后能够重合,则这些函数为“互为生成函数”.下列函数中,与
构成“互为生成函数”的有( )
A. B.
第6页/共16页
学科网(北京)股份有限公司C. D.
【答案】AC
【解析】
【分析】由三角恒等变换,化简函数的解析式,再根据三角函数的平移变换规律,得出结论.
【详解】 ,由 ,
则将 的图象向左平移 个单位长度后,即可与 的图象重合;
由 ,
则 图象无法经过平移与 的图象重合;
由 ,
则将 的图象向左平移 个单位长度后,再向下平移1个单位长度后,
即可与 的图象重合;
由 ,则 的图象无法经过平移与 的图象重合.
故A,C中的函数与 “互为生成函数”.
故选:AC
三、填空题:本大题共3小题,每小题5分,共15分.
12. 在一个样本的频率分布直方图中,共有5个小矩形,若中间一个小矩形的面积等于其他4个小矩形的
面积和的 ,且中间一组的频数为25,则样本容量为_____.
【答案】100
【解析】
第7页/共16页
学科网(北京)股份有限公司【分析】根据频率和为1求中间一组的频率,结合频数求样本容量.
【详解】设中间一组的频率为 ,
由题意可知: ,解得 ,
又因为中间一组的频数为25,所以样本容量为 .
故答案为:100.
13. 在复平面内,复数 与 所对应的向量分别为 和 ,其中 为坐标原点,则 对应的
复数为_______
【答案】 ##
【解析】
【分析】先利用复数的几何意义求出 和 的坐标,从而求出 的坐标,由此得解.
【详解】因为复数 与 所对应的向量分别为 和 ,
所以 , ,
所以 ,即 对应的复数为 .
故答案为:
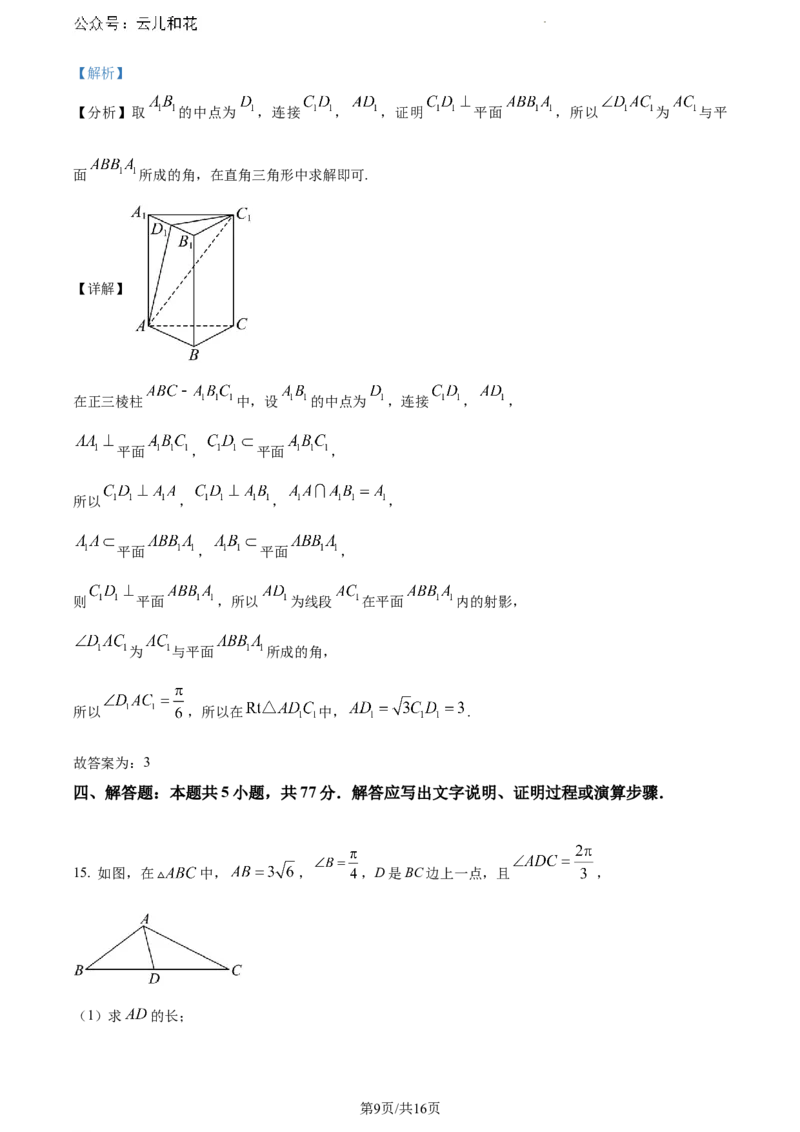
14. 如图,正三棱柱 的底面边长为2, 与平面 所成角的大小为 ,则线段
在平面 内的射影长为______.
【答案】3
第8页/共16页
学科网(北京)股份有限公司【解析】
【分析】取 的中点为 ,连接 , ,证明 平面 ,所以 为 与平
面 所成的角,在直角三角形中求解即可.
【详解】
在正三棱柱 中,设 的中点为 ,连接 , ,
平面 , 平面 ,
所以 , , ,
平面 , 平面 ,
则 平面 ,所以 为线段 在平面 内的射影,
为 与平面 所成的角,
所以 ,所以在 中, .
故答案为:3
四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.
15. 如图,在 中, , ,D是BC边上一点,且 ,
(1)求 的长;
第9页/共16页
学科网(北京)股份有限公司(2)若 ,求 .
【答案】(1)
(2)
【解析】
在
【分析】(1) 中,利用正弦定理即可得解;
(2)在 中,先利用余弦定理求得 ,再利用正弦定理即可得解.
【小问1详解】
在 中, ,则 ,
在 中, ,即 ,得 .
【小问2详解】
因为在 中, ,
所以 ,
则 ,
又 ,即 ,解得 ,
所以 .
16. 计算机考试分理论考试与实际操作两部分,每部分考试成绩只记“合格”与“不合格”,两部分考试
都“合格”者,则计算机考试“合格”,并颁发合格证书甲、乙、丙三人在理论考试中“合格”的概率依
第10页/共16页
学科网(北京)股份有限公司次为 , , ,在实际操作考试中“合格”的概率依次为 , , ,所有考试是否合格相互之间没
有影响.
(1)假设甲、乙、丙三人同时进行理论与实际操作两项考试,谁获得合格证书的可能性最大?
(2)这三人进行理论与实际操作两项考试后,求恰有两人获得合格证书的概率.
【答案】(1)丙;(2)
【解析】
【分析】
(1)分别计算三者获得合格证书的概率,比较大小即可(2)根据互斥事件的和,列出三人考试后恰有两人
获得合格证书事件,由概率公式计算即可求解.
【详解】(1)设“甲获得合格证书”为事件A,“乙获得合格证书”为事件B,“丙获得合格证书”为事
件C,则 , , .
因为 ,所以丙获得合格证书的可能性最大.
(2)设“三人考试后恰有两人获得合格证书”为事件D,则
.
【点睛】本题主要考查了相互独立事件,互斥事件,及其概率公式的应用,属于中档题.
17. 记 的内角A,B,C的对边分别为a,b,c,向量
且 .
(1)求角C的大小;
(2)若 的面积 ,求c.
【答案】(1)
第11页/共16页
学科网(北京)股份有限公司(2)
【解析】
【分析】(1)利用向量垂直的坐标表示,结合正弦定理的边角变换与余弦定理即可得解;
(2)利用三角形面积公式得到 ,利用三角函数的和差公式得到 ,再利用正弦定理即可得解.
【小问1详解】
因为 , , ,
所以 ,
由正弦定理得 ,化简得 ,
所以 ,
又 ,所以 .
【小问2详解】
由题意得 ,则 ,
由 ,
得 ,则 ,
因为 ,所以 ,
所以 .
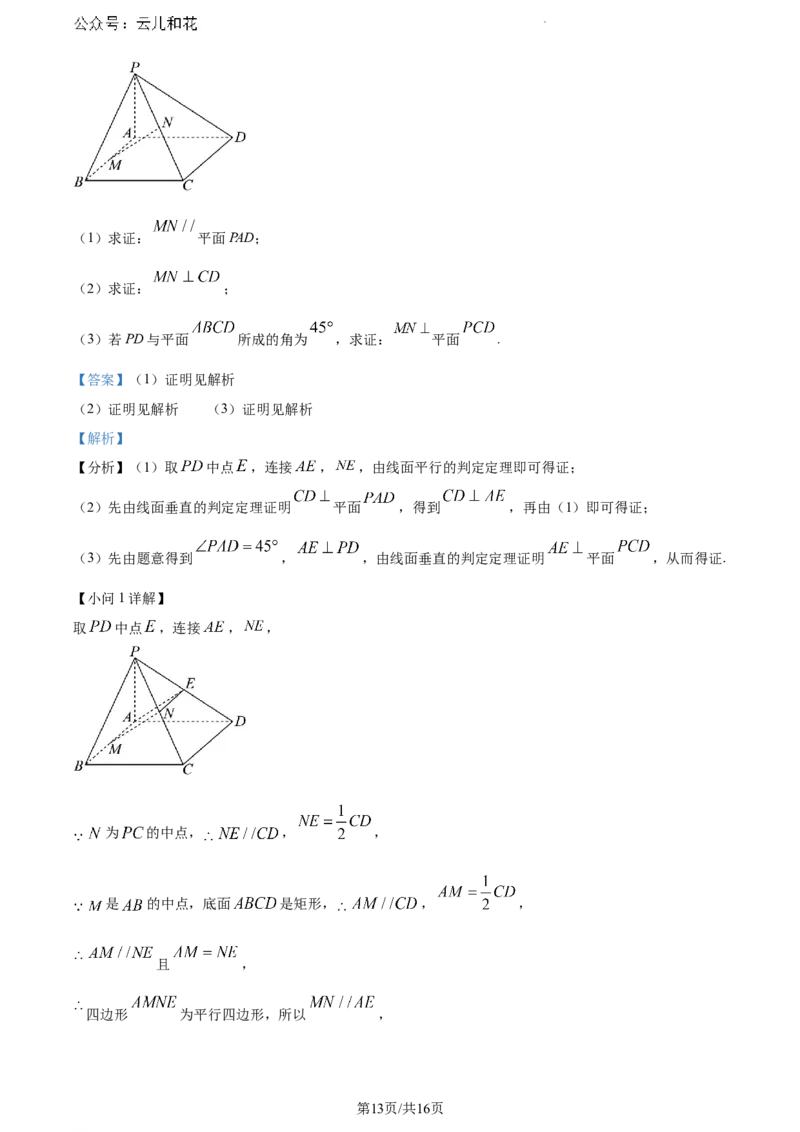
18. 在四棱锥 中,底面 是矩形, 平面 , 分别是 的中点.
第12页/共16页
学科网(北京)股份有限公司(1)求证: 平面PAD;
(2)求证: ;
(3)若PD与平面 所成的角为 ,求证: 平面 .
【答案】(1)证明见解析
(2)证明见解析 (3)证明见解析
【解析】
【分析】(1)取 中点 ,连接 , ,由线面平行的判定定理即可得证;
(2)先由线面垂直的判定定理证明 平面 ,得到 ,再由(1)即可得证;
(3)先由题意得到 , ,由线面垂直的判定定理证明 平面 ,从而得证.
【小问1详解】
取 中点 ,连接 , ,
为 的中点, , ,
是 的中点,底面 是矩形, , ,
且 ,
四边形 为平行四边形,所以 ,
第13页/共16页
学科网(北京)股份有限公司又 平面 , 平面 ,
平面 .
【小问2详解】
平面 , 平面 , ,
又 底面 是矩形, ,
又 平面 , 平面 ,
平面 , ,
由(1)可知 , .
【小问3详解】
平面 ,所以 为 与平面 所成的角,
,又 , ,即 为等腰三角形,
为 中点, ,
又由(2)可得 , 平面 ,
平面 ,
由(1)可知: , 平面 .
19. 图1所示的是等腰梯形ABCD,AB//CD,AB=3,CD=1, ,DE⊥AB于E点,现将△ADE
沿直线DE折起到△PDE的位置,连接PB,PC,形成一个四棱锥P-EBCD,如图2所示.
第14页/共16页
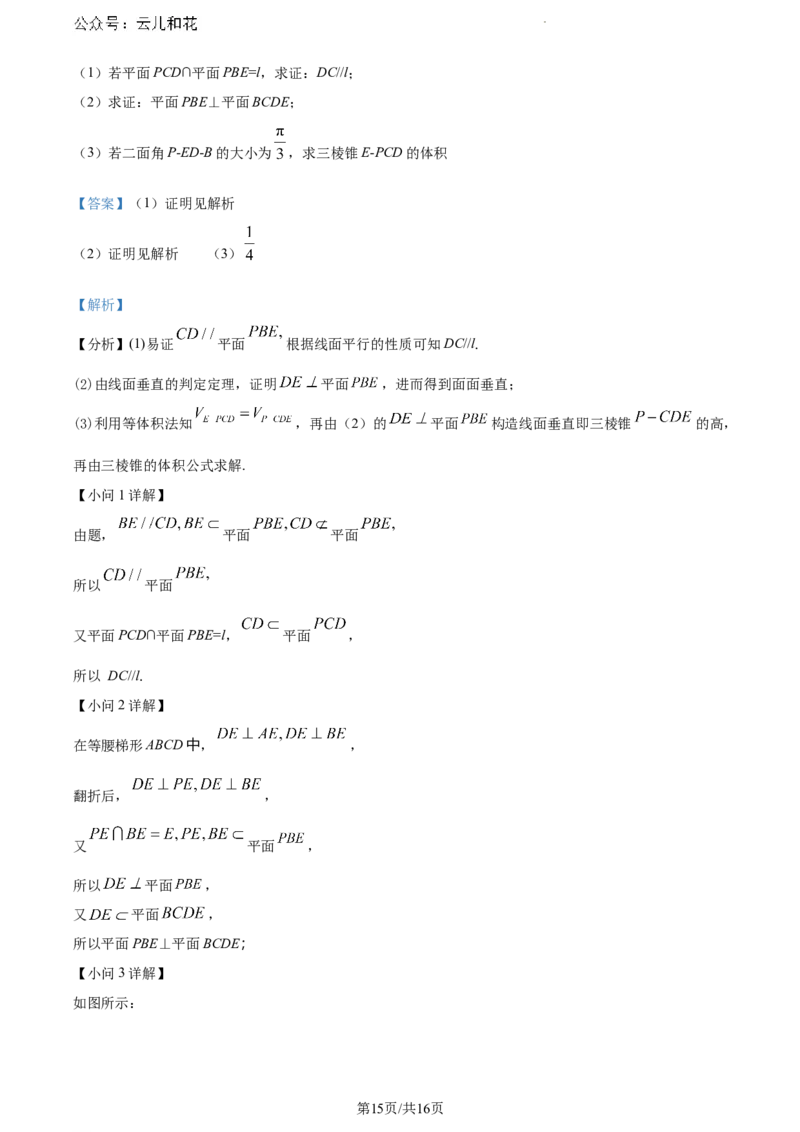
学科网(北京)股份有限公司(1)若平面PCD∩平面PBE=l,求证:DC//l;
(2)求证:平面PBE⊥平面BCDE;
(3)若二面角P-ED-B的大小为 ,求三棱锥E-PCD的体积
【答案】(1)证明见解析
(2)证明见解析 (3)
【解析】
【分析】(1)易证 平面 根据线面平行的性质可知DC//l.
(2)由线面垂直的判定定理,证明 平面 ,进而得到面面垂直;
(3)利用等体积法知 ,再由(2)的 平面 构造线面垂直即三棱锥 的高,
再由三棱锥的体积公式求解.
【小问1详解】
由题, 平面 平面
所以 平面
又平面PCD∩平面PBE=l, 平面 ,
所以 DC//l.
【小问2详解】
在等腰梯形ABCD中, ,
翻折后, ,
又 平面 ,
所以 平面 ,
又 平面 ,
所以平面PBE⊥平面BCDE;
【小问3详解】
如图所示:
第15页/共16页
学科网(北京)股份有限公司根据等腰梯形易知,
因为 ,
所以 即为二面角 的平面角, ,
在 中,由余弦定理可知: ,
故 ,
过点P作 交BE于点F,在 中由等面积法可知:
则 ,
由(2)知, 平面 ,且 平面 ,
所以 ,
又 , 平面 ,
所以 平面BCDE,
所以 .
第16页/共16页
学科网(北京)股份有限公司