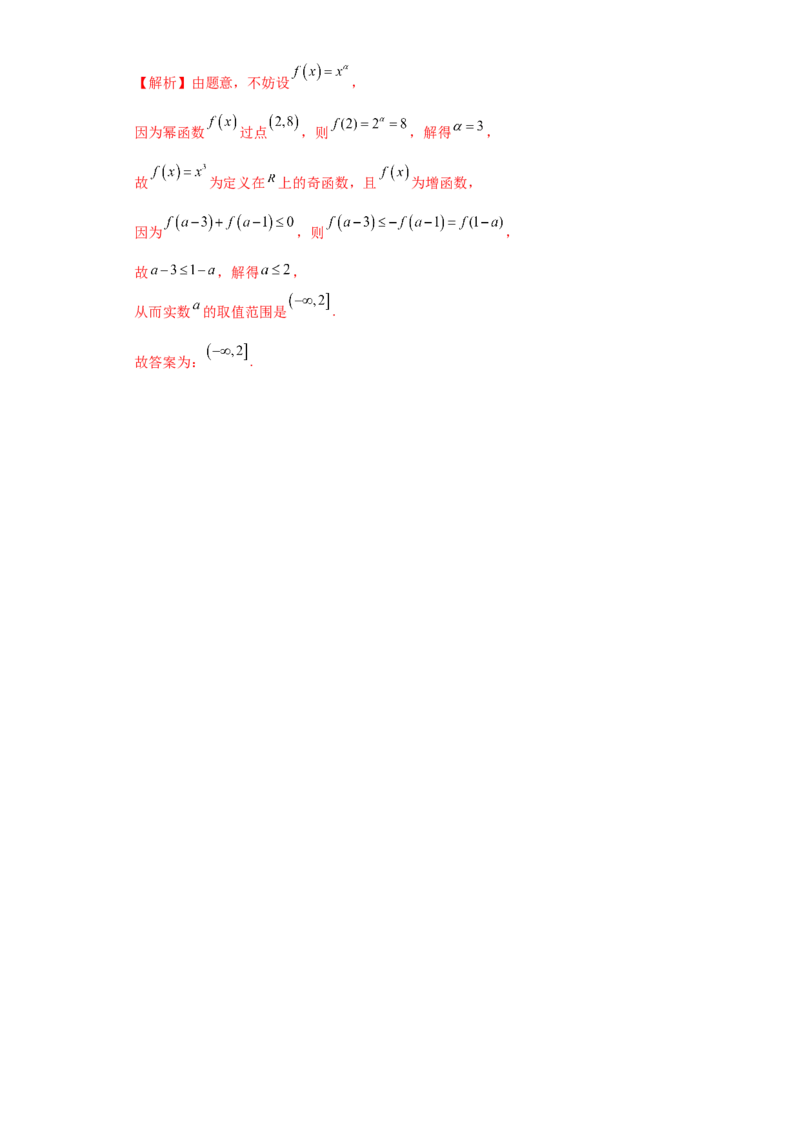文档内容
专题 3.3 幂函数
1 幂函数的定义
一般地,形如y=xα的函数称为幂函数,其中x是自变量,α为常数.
注 (1)注意幂函数中xα的系数是1,底数是变量x,指数α是常数;
2正数的正分数指数幂的意义
(1)正数的正分数指数幂的意义,规定: m
an =√n am (a>0,m,n∈N∗,且n>1)
巧记“子内母外”(根号内的m作分子,根号外的n作为分母)
m
− 1 1
(2)正数的正分数指数幂的意义:a n = = (a>0,m,n∈N∗,且n>1)
m √n am
an
(3)0的正分数指数幂等于0,0的负分数指数幂没有意义.
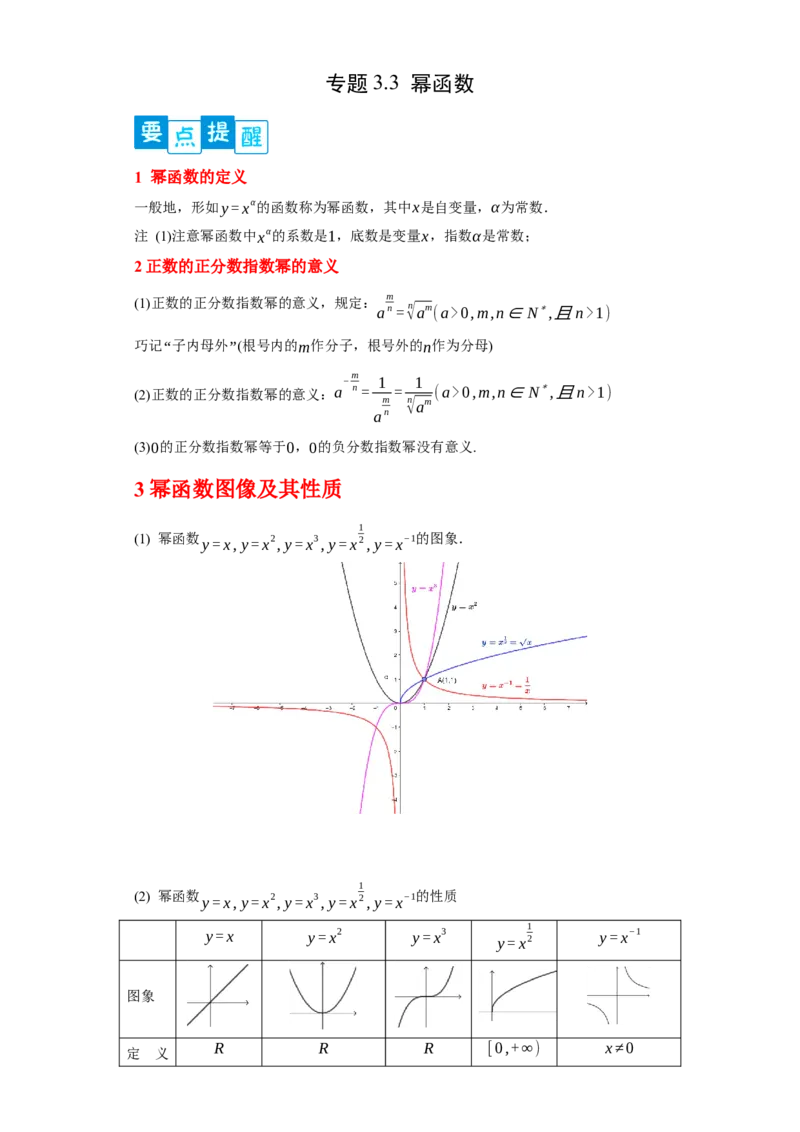
3 幂函数图像及其性质
1
(1) 幂函数 y=x,y=x2,y=x3,y=x2,y=x−1的图象.
1
(2) 幂函数 y=x,y=x2,y=x3,y=x2,y=x−1的性质
1
y=x y=x2 y=x3
y=x2
y=x−1
图象
X|X|K]
定 义
R R R [0,+∞) x≠0域
值域 R [0,+∞) R [0,+∞) x≠0
奇 偶
奇函数 偶函数 奇函数 非奇非偶 奇函数
性
在 (−∞,0]上 递 在 (−∞,0)上 递
单 调 在[0,+∞)
在R上递增 减 在R上递增 减
性 上递增
在(0,+∞)上递增 在(0,+∞)上递减
定点 (1,1),(0,0) (1,1),(0,0) (1,1),(0,0) (1,1),(0,0) (1,1)
(3)性质
① 所有的幂函数在(0 , +∞ )都有定义,并且图象都过点(1 , 1);
② α>0时,幂函数的图象通过原点,并且在[0 , +∞ )上是增函数.
特别地,当α>1时,幂函数变化快,图象下凹;当0<α<1时,幂函数变化慢,图象上
凸.
③ α<0时,幂函数的图象在(0 , +∞ )上是减函数.在第一象限内,当x从右边趋
向原点时,图象在y轴右方无限地逼近y轴正半轴,当x趋于+∞时,图象在x轴上方无
限地逼近x轴正半轴.
一、单选题
1.幂函数 在 上单调递减,则实数m的值为( )
A. B.3 C. 或3 D.
【答案】A
【解析】因为 是幂函数,
故 ,解得 或 ,
又因为幂函数在 上单调递减,所以需要 ,则 故选:A
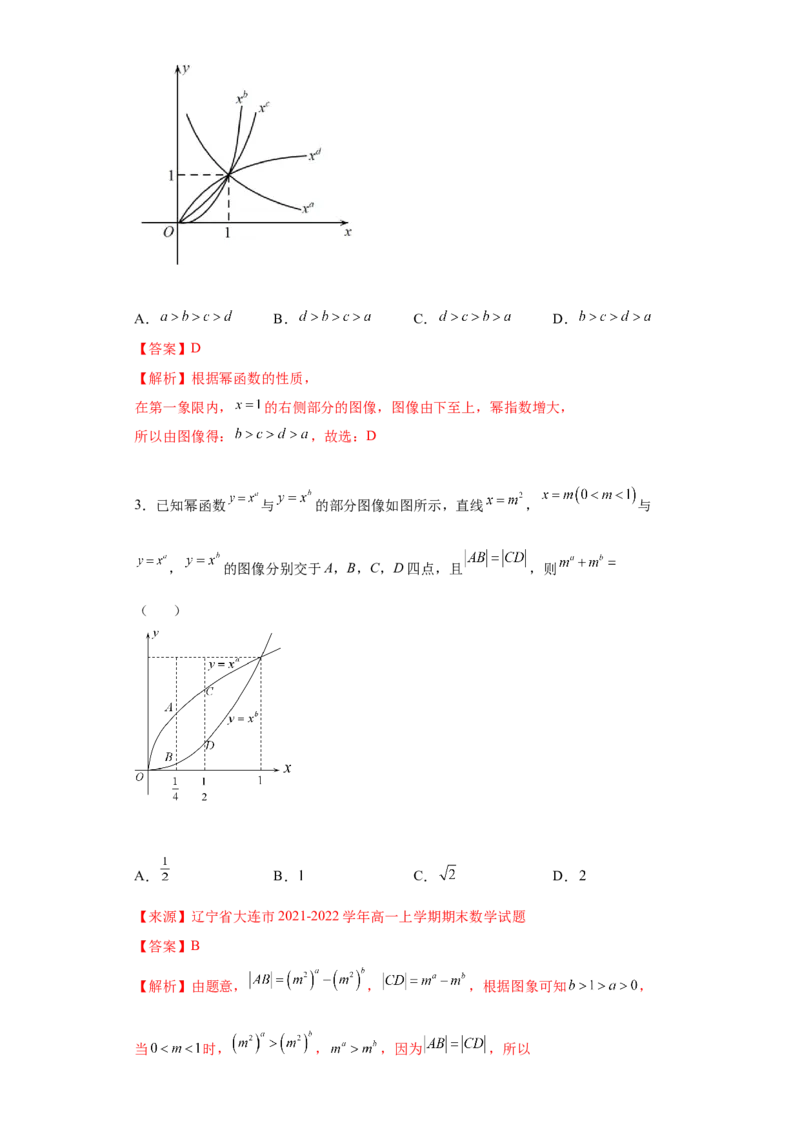
2.幂函数 在第一象限的图像如图所示,则 的
大小关系是 ( )A. B. C. D.
【答案】D
【解析】根据幂函数的性质,
在第一象限内, 的右侧部分的图像,图像由下至上,幂指数增大,
所以由图像得: ,故选:D
3.已知幂函数 与 的部分图像如图所示,直线 , 与
, 的图像分别交于A,B,C,D四点,且 ,则
( )
A. B. C. D.
【来源】辽宁省大连市2021-2022学年高一上学期期末数学试题
【答案】B
【解析】由题意, , ,根据图象可知 ,
当 时, , ,因为 ,所以,因为 ,可得 .故选:B
4.已知幂函数 在 上单调递减,设 ,
, ,则( )
A. B.
C. D.
【来源】广东省梅州市2021-2022学年高一上学期期末数学试题
【答案】C 根据幂函数的定义可得 ,解得 或 ,
当 时, ,此时满足 在 上单调递增,不合题意,
当 时, ,此时 在 上单调递减,
所以 .因为 ,
又 ,所以 ,
因为 在 上单调递减,所以 ,
又因为 为偶函数,所以 ,
所以 .故选:C
5.设 , , , ,则这四个数的大小关系是( )
A. B. C. D.
【来源】广东省湛江市2021-2022学年高一下学期期末数学试题
【答案】B
【解析】:∵ ,∴ ,
又 ,∴ ,故 .故选:B.
6.设 , , ,则( )
A. B. C. D.
【来源】广东省广雅中学2021-2022学年高一上学期期末数学试题
【答案】B
【解析】 是增函数,
,
是减函数, 在 上是增函数,
故选:B
7.已知函数 ,若 ,则实数a的取值范围是
( )
A. B. C. D.
【答案】A
【解析】设 , ,则
,即 为奇函数,容易判
断 在R上单调递增(增+增),又 可化为,
,所以a >1-2a,∴ a >
.
故选:A.8.幂函数 在区间 上单调递增,且 ,则
的值( )
A.恒大于0 B.恒小于0
C.等于0 D.无法判断
【来源】青海省西宁市大通回族土族自治县2021-2022学年高一上学期期末考试数学
试题
【答案】A
【解析】由函数 是幂函数,可得 ,解得 或
.
当 时, ;当 时, .
因为函数 在 上是单调递增函数,故 .
又 ,所以 ,
所以 ,则 .
故选:A.
9.已知函数 是减函数,则实数a的取值范围是( )
A. B. C. D.
【答案】B
【解析】因为函数 是减函数,
所以幂函数 为减函数,一次函数 为减函数,
所以 ,解得: ,
所以实数a的取值范围是
故选:B10.设 ,若 ,则
A.2 B.4 C.6 D.8
【来源】第13讲 函数的表示方法-【暑假自学课】2022年新高一数学暑假精品课(苏
教版2019必修第一册)
【答案】C
【解析】由 时 是增函数可知,若 ,则 ,所以 ,
由 得 ,解得 ,则 ,故选C.
11.函数 的图象如图所示,则下列结论成立的是
A. , ,
B. , ,
C. , ,
D. , ,
【来源】江西省丰城中学2021-2022学年高一下学期入学考试数学试题
【答案】C
【解析】试题分析:函数在 处无意义,由图像看 在 轴右侧,所以 ,
,由 即 ,即函数的零点
,故选C.12.函数 是幂函数,对任意 ,且 ,满足
,若 ,且 ,则 的值( )
A.恒大于0 B.恒小于0 C.等于0 D.无法判断
【答案】A
【解析】由已知函数 是幂函数,
可得 ,解得 或 ,当 时, ,当 时,
,
对任意的 ,且 ,满足 ,
函数是单调增函数,所以 ,此时 ,
又 ,可知 异号,且正数的绝对值大于负数的绝对值,
则 恒大于 ,故选A.
13.已知 是定义域为 的奇函数,满足 .若 ,则
A. B. C. D.
【来源】宁夏石嘴山市平罗中学2021-2022学年高一上学期期末考试数学试题
【答案】C
【解析】:因为 是定义域为 的奇函数,且 ,
所以 ,
因此 ,
因为 ,所以 ,
,从而 ,选C.14.若幂函数 的图象过点 ,则函数 的最大值为
( )
A. B. C. D.
【答案】C
【解析】设幂函数 ,
因为函数 的图象过点 ,
所以 ,所以 ,故 ,
所以 .
令 ,所以 ,
则 ,
所以当 时, . 故选:C.
二、填空题
15.已知幂函数 在 上单调递减,则 ______.
【来源】河北省安新中学2021-2022学年高一上学期期末数学试题
【答案】 ##
【解析】:由题意得 且 ,则 , ,故 .
故答案为:
16.已知幂函数 的图像关于y轴对称,且在 上是减函
数,实数 满足 ,则 的取值范围是_____.
【答案】【解析】 幂函数 在 上是减函数,
,解得 ,
, 或 .当 时, 为偶函数满足条件,
当 时, 为奇函数不满足条件,
则不等式等价为 ,即 ,
在R上为增函数, ,解得: .故答案为: .
17.写出一个同时具有下列性质①②③的函数 ______.
① ;② ;③任取 , , 且
.
【答案】 (答案不唯一)
【解析】取 ,函数 为幂函数,满足①; ,则函数
为偶函数,满足②;③表示函数 在 上单调递增,由幂函数的性质可
知 满足③.
故答案为: (答案不唯一)
18.已知 是奇函数,当 时, ,则 ______.
【来源】山东省济宁市2021-2022学年高一上学期期末数学试题
【答案】-4
【解析】因为 是奇函数,当 时, ,
所以 ,得 ,所以 , ,
因为 是奇函数
所以 ,
故答案为:
19.已知幂函数 的图象关于 轴对称,且在 上单调递减,
则满足 的 的取值范围为________.
【答案】
【解析】幂函数 在 上单调递减,故 ,解得
.
,故 , , .
当 时 , 不关于 轴对称,舍去;
当 时 , 关于 轴对称,满足;
当 时 , 不关于 轴对称,舍去;
故 , ,函数 在 和 上单调递减,
故 或 或 ,解得 或 .
故答案为:
20.若幂函数 过点 ,则满足不等式 的实数 的取值范
围是______
【来源】重庆市巫山县官渡中学等两校2021-2022学年高一上学期期末数学试题
【答案】【解析】由题意,不妨设 ,
因为幂函数 过点 ,则 ,解得 ,
故 为定义在 上的奇函数,且 为增函数,
因为 ,则 ,
故 ,解得 ,
从而实数 的取值范围是 .
故答案为: .