文档内容
专题 3.4 函数的应用
1.一次函数模型的应用
一次函数模型:f(x)=kx+b(k,b为常数,k≠0).
一次函数是常见的一种函数模型,在初中就已接触过.
2.二次函数模型的应用
二次函数模型:f(x)= +bx+c(a,b,c为常数,a≠0).
二次函数为生活中常见的一种数学模型,因二次函数可求其最大值(或最小值),故最优、
最省等最值
问题常用到二次函数模型.
3.幂函数模型的应用
幂函数模型应用的求解策略
(1)给出含参数的函数关系式,利用待定系数法求出参数,确定函数关系式.
(2)根据题意,直接列出相应的函数关系式.
4.分段函数模型的应用
由于分段函数在不同区间上具有不同的解析式,因此分段函数在研究条件变化前后的
实际问题中具有广泛的应用.
5.“对勾”函数模型的应用
对勾函数模型是常考的模型,要牢记此类函数的性质,尤其是单调性:y=ax+
(a>0,b>0),当x>0时,在(0, ]上递减,在( ,+ )上递增.另外,还要注意换元法
的运
一、单选题
1.已知函数 ,则函数 的图象可能是( )
A. B. C. D.【来源】宁夏石嘴山市平罗中学2021-2022学年高一上学期期末考试数学试题
【答案】B 易知函数 的图象的分段点是 ,且
过点 , ,又 ,故选:B.
2.设函数 ,则满足 的 的取值范围是( )
A. B. C. D.
【来源】黑龙江省七台河市勃利县高级中学2021-2022学年高一上学期期末考试数学
试题
【答案】D因为 ,
当 时, 显然单调递减;当 时, 也是单调递减;
且 ,即函数图像连续不断,
所以 在其定义域上单调递减,
由 可得 ,解得 .故选:D.
3.根据表格中的数据,可以断定方程 的一个根所在的区间是(
)
x -1 0 1 2 3
ex 0.37 1 2.72 7.40 20.12
x+2 1 2 3 4 5A.(-1,0) B.(0,1) C.(1,2) D.(2,3)
【来源】重庆市巫山县官渡中学等两校2021-2022学年高一上学期期末数学试题
【答案】C
【解析】设函数 ,
, ,
,又 在区间(1,2)连续,
函数 在区间(1,2)存在零点,
方程根所在的区间为(1,2),故选:C.
4.已知函数 ,若实数 ,则函数 的零点个数
为( )
A.0 B.1 C.2 D.3
【来源】黑龙江省双鸭山市集贤县2021-2022学年高一上学期期末数学试题
【答案】D
【解析】令 ,得 ,根据分段函数 的解析式,做出函数
的图象,如下图所示,因为 ,由图象可得出函数 的零点
个数为3个,故选:D.
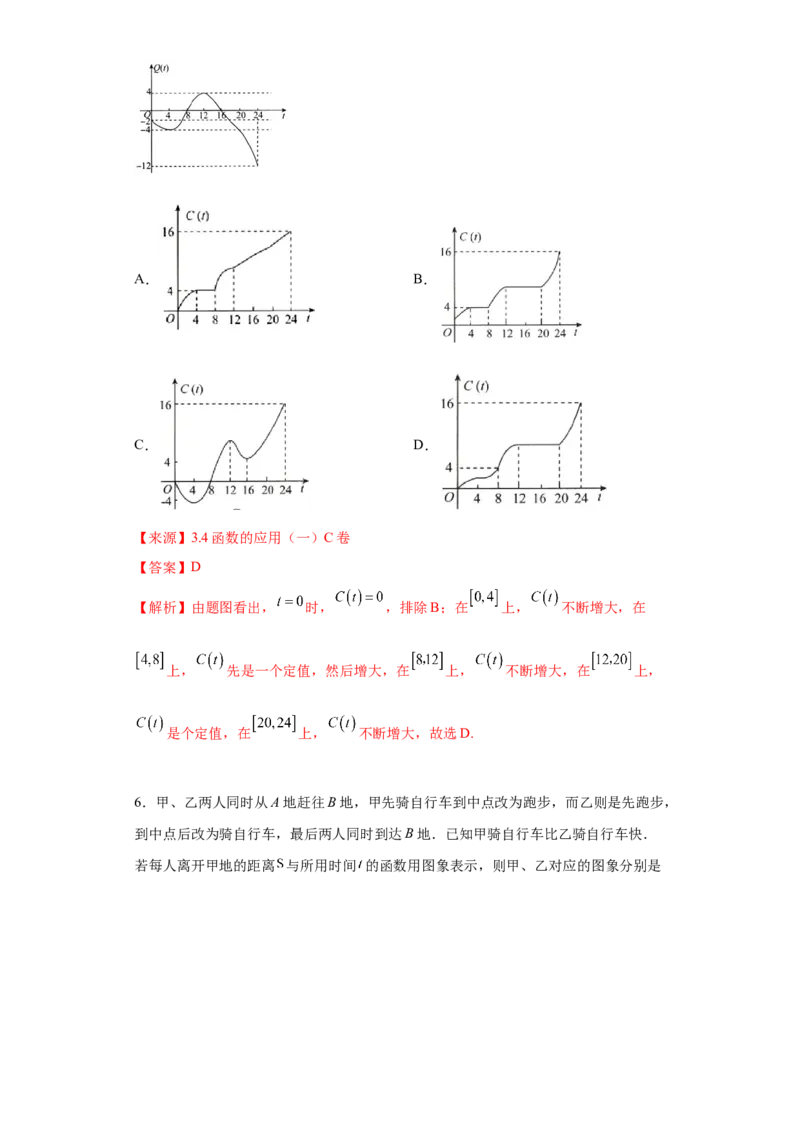
5.某地一天内的气温 (单位: )与时刻 (单位: )之间的关系如图所示,
令 表示时间段 内的温差(即时间段内最高温度与最低温度的差),则 与
之间的函数图像大致是A. B.
C. D.
【来源】3.4函数的应用(一)C卷
【答案】D
【解析】由题图看出, 时, ,排除B;在 上, 不断增大,在
上, 先是一个定值,然后增大,在 上, 不断增大,在 上,
是个定值,在 上, 不断增大,故选D.
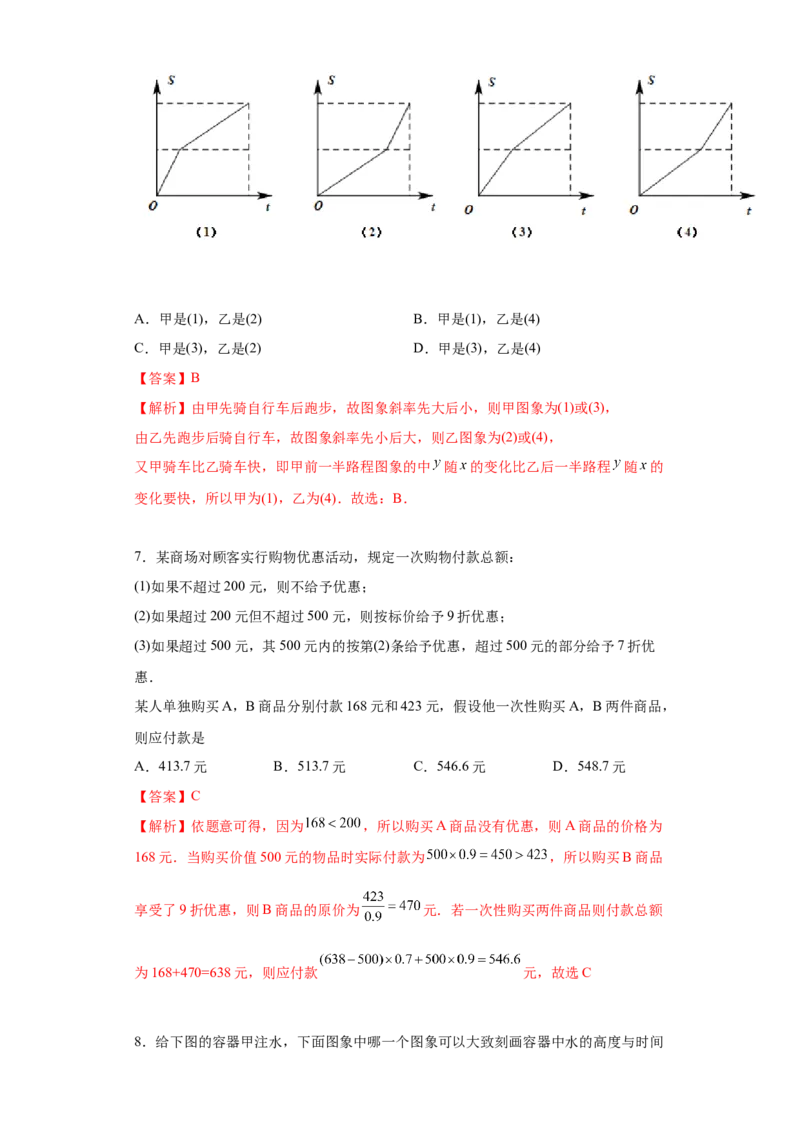
6.甲、乙两人同时从A地赶往B地,甲先骑自行车到中点改为跑步,而乙则是先跑步,
到中点后改为骑自行车,最后两人同时到达B地.已知甲骑自行车比乙骑自行车快.
若每人离开甲地的距离 与所用时间 的函数用图象表示,则甲、乙对应的图象分别是A.甲是(1),乙是(2) B.甲是(1),乙是(4)
C.甲是(3),乙是(2) D.甲是(3),乙是(4)
【答案】B
【解析】由甲先骑自行车后跑步,故图象斜率先大后小,则甲图象为(1)或(3),
由乙先跑步后骑自行车,故图象斜率先小后大,则乙图象为(2)或(4),
又甲骑车比乙骑车快,即甲前一半路程图象的中 随 的变化比乙后一半路程 随 的
变化要快,所以甲为(1),乙为(4).故选:B.
7.某商场对顾客实行购物优惠活动,规定一次购物付款总额:
(1)如果不超过200元,则不给予优惠;
(2)如果超过200元但不超过500元,则按标价给予9折优惠;
(3)如果超过500元,其500元内的按第(2)条给予优惠,超过500元的部分给予7折优
惠.
某人单独购买A,B商品分别付款168元和423元,假设他一次性购买A,B两件商品,
则应付款是
A.413.7元 B.513.7元 C.546.6元 D.548.7元
【答案】C
【解析】依题意可得,因为 ,所以购买A商品没有优惠,则A商品的价格为
168元.当购买价值500元的物品时实际付款为 ,所以购买B商品
享受了9折优惠,则B商品的原价为 元.若一次性购买两件商品则付款总额
为168+470=638元,则应付款 元,故选C
8.给下图的容器甲注水,下面图象中哪一个图象可以大致刻画容器中水的高度与时间的函数关系:().
A. B.
B.C. D.
【来源】3.4函数的应用(一)B卷
【答案】B试题分析:容器下端较窄,上端较宽,当均匀的注入水时,刚开始的一段
时间高度变化较大,随时时间的推移,高度的变化速度开始减小,即高度变化不太明
显,四个图像中只有B项符合特点
二、解答题
9.2022年第24届北京冬季奥林匹克运动会,于2022年2月4日星期五开幕,将于2
月20日星期日闭幕.该奥运会激发了大家对冰雪运动的热情,与冰雪运动有关的商品
销量持续增长.对某店铺某款冰雪运动装备在过去的一个月内(以30天计)的销售情
况进行调查发现:该款冰雪运动装备的日销售单价 (元/套)与时间x(被调查的
一个月内的第x天)的函数关系近似满足 (k为正常数).该商品的日销售
量 (个)与时间x(天)部分数据如下表所示:
x 10 20 25 30
110 120 125 120已知第10天该商品的日销售收入为121元.
(1)求k的值;
(2)给出两种函数模型:① ,② ,请你根据上表中的数
据,从中选择你认为最合适的一种函数来描述该商品的日销售量 与时间x的关系,
并求出该函数的解析式;
(3)求该商品的日销售收入 ( , )(元)的最小值.
【答案】(1) (2)选择②, ,( , )(3)121元
【解析】(1)
因为第10天该商品的日销售收入为121元,
所以 ,解得 ;
(2)由表中数据可得,当时间变化时,该商品的日销售量有增有减,并不单调,
故只能选②:
代入数据可得: ,解得 , ,
所以 ,( , )
(3)由(2)可得, ,
所以, ,
所以当 , 时, 在区间 上单调递减,在区间
上单调递增,
所以当 时, 有最小值,且为121;
当 , 时, 为单调递减函数,
所以当 时, 有最小值,且为124,综上,当 时, 有最小值,且为121元,
所以该商品的日销售收入最小值为121元.
10.提高过江大桥的车辆通行能力可改善整个城市的交通状况.在一般情况下,大桥
上的车流速度 (单位:千米/小时)是车流密度 (单位:辆/千米)的函数.当桥上的的车
流密度达到200辆/千米时,造成堵塞,此时车流速度为0;当车流密度不超过20辆/千
米时,车流速度为60千米/小时,研究表明;当 时,车流速度 是车流密
度 的一次函数.
(1)当 时,求函数 的表达式;
(2)当车流密度 为多大时,车流量(单位时间内通过桥上某观点的车辆数,单位:辆/每
小时) 可以达到最大,并求出最大值(精确到1辆/小时)﹒
【答案】(1) ;
(2)当车流密度为100辆/千米时,车流量可以达到最大,最大值约为3333辆/小时.
【解析】当 时, ;
当 时,设 ,
由已知得 解得 ,
故函数 的表达式为 ;
(2)依题意并由(1)可得 ,
当 时, 为增函数,故当 时,其最大值为60×20=1200;
当 时, ,
∴当 时, 在区间(20,200]上取得最大值 ,
∵3333>1200,∴当车流密度为100辆/千米时,车流量可以达到最大,最大值约为3333辆/小时.
11.某地空气中出现污染,须喷洒一定量的去污剂进行处理,据测算,每喷洒1个单
位的去污剂,空气中释放的浓度 (单位:毫克/立方米)随着时间 (单位:天)变化的函
数关系式近似为 ,若多次喷洒,则某一时刻空气中的去污剂浓度
为每次投放的去污剂在相应时刻所释放的㳖度之和,由实验知,当空气中去污剂的浓
度不低于4(毫克/立方米)时,它才能起到去污作用.
(1)若一次喷洒4个单位的去污剂,则去污时间可达几天?
(2)若第一次喷洒2个单位的去污剂,6天后再喷洒 个单位的去污剂,要使接
下来的4天中能够持续有效去污,试求 的最小值.(精确到0.1,参考数据: 取1.4)
【答案】(1) 天(2)
【解析】(1)解:∵一次喷洒 个单位的净化剂,
∴浓度 ,
则当 时,由 ,解得 ,
∴此时 .
当 时,由 ,解得 ,
∴此时 .
综合得 ,
若一次投放 个单位的制剂,则有效净化时间可达 天.
(2)解:设从第一次喷洒起,经 天,
浓度 ,
∵ ,而 ,
∴ ,故当且仅当 时, 有最小值为 .
令 ,解得 ,
∴ a的最小值为 .
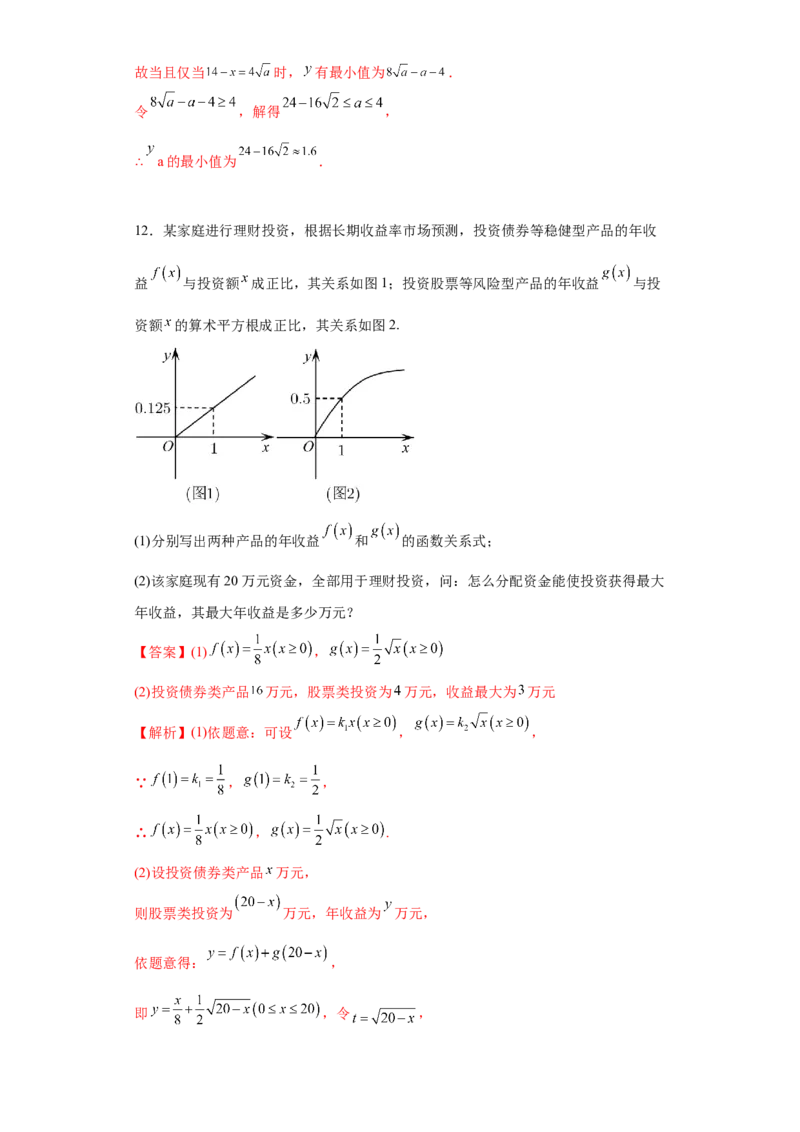
12.某家庭进行理财投资,根据长期收益率市场预测,投资债券等稳健型产品的年收
益 与投资额 成正比,其关系如图1;投资股票等风险型产品的年收益 与投
资额 的算术平方根成正比,其关系如图2.
(1)分别写出两种产品的年收益 和 的函数关系式;
(2)该家庭现有20万元资金,全部用于理财投资,问:怎么分配资金能使投资获得最大
年收益,其最大年收益是多少万元?
【答案】(1) ,
(2)投资债券类产品 万元,股票类投资为 万元,收益最大为 万元
【解析】(1)依题意:可设 , ,
∵ , ,
∴ , .
(2)设投资债券类产品 万元,
则股票类投资为 万元,年收益为 万元,
依题意得: ,
即 ,令 ,则 , ,
则 , ,
所以当 ,即 万元时,
收益最大, 万元.
13.新冠肺炎疫情造成医用防护服短缺,某地政府决定为防护服生产企业 公司扩大
生产提供 ( )(万元)的专项补贴,并以每套80元的价格收购其生产的全
部防护服, 公司在收到政府 (万元)补贴后,防护服产量将增加到
(万件),其中 为工厂工人的复工率( ), 公司生产
万件防护服还需投入成本 (万元).
(1)将 公司生产防护服的利润 (万元)表示为补贴 (万元)的函数(政府补贴
万元计入公司收入);
(2)当复工率 时,政府补贴多少万元才能使 公司的防护服利润达到最大?并求
出最大值.
【来源】江西省新余市2021-2022学年高一上学期期末数学试题
【答案】(1) , ,
(2)当复工率 时,政府补贴2万元才能使 公司的防护服利润达到最大值60万元
【解析】(1)由题意得
,
即 , , .
(2)由 ,得 ,
因 ,当且仅当 时取等号,所以
.故当复工率 时,政府补贴2万元才能使 公司的防护服利润达到最大值60万元.
14.已知函数 是幂函数.
(1)求函数 的解析式;
(2)判断函数 的奇偶性,并证明你的结论;
(3)判断函数 在 上的单调性,并证明你的结论.
【答案】(1) ;(2)函数 为偶函数;(3) 在 上单调递减,证明见解
析.(1)因为函数 是幂函数,
则 ,解得 ,故 .
(2)函数 为偶函数.
证明如下:由(1)知 ,其定义域为 关于原点对称,
因为对于定义域内的任意 ,都有
,故函数 为偶函数.
(3) 在 上单调递减.
证明如下:在 上任取 , ,不妨设 ,则
,
且 , ,
在 上单调递减.