专题33二项分布与超几何分布（原卷版）_E015高中全科试卷_数学试题_选修3_05.专项训练_专题33二项分布与超几何分布-高中数学新教材人教A版选择性必修配套提升训练

专题33 二项分布与超几何分布 一、单选题 1．（2020·山西应县一中高二期中（理））盒中有10个螺丝钉,其中有3个是坏的,现从盒中随机地抽取4 3 个,那么概率是10的事件为( ) A．恰有1个是坏的 B．4个全是好的 C．恰有2个是好的 D．至多有2个是坏的 2．（2020·天山 新疆实验高二期末）有10件产品，其中3件是次品，从中任取两件，若X表示取得次品 的个数，则P(X2)等于（ ） 7 8 A．15 B．15 14 C．15 D．1 7 3 3 3．（2020·江苏鼓楼 南京师大附中高二期末）某地 个贫困村中有 个村是深度贫困，现从中任意选 个 6 村，下列事件中概率等于7 的是（ ） A．至少有1个深度贫困村 B．有1个或2个深度贫困村 2 3 2 C．有 个或 个深度贫困村 D．恰有 个深度贫困村 10 6 4 4 4．（2020·辉县市第二高级中学高二月考（理））在 个排球中有 个正品， 个次品.从中抽取 个，则 正品数比次品数少的概率为（ ） 5 4 19 8 A．42 B．35 C．42 D．215．（2020·营口市第二高级中学高二期末）荷花池中，有一只青蛙在成“品”字形的三片荷叶上跳来跳去 （每次跳跃时，均从一片荷叶跳到另一片荷叶），而且逆时针方向跳的概率是顺时针方向跳的概率的两倍， 如图所示.假设现在青蛙在A荷叶上，则跳三次之后停在A荷叶上的概率是（ ） 2 1 1 3 A．3 B．4 C．3 D．4  6．（2020·科尔沁左翼后旗甘旗卡第二高级中学高二期末（理））已知随机变量 服从二项分布  1 B 4,    3，则P(3)（ ）． 32 16 24 8 A．81 B．81 C．81 D．81 7．（2020·青铜峡市高级中学高二期末（理））有8件产品，其中4件是次品，从中有放回地取3次（每 P(X 2) 次1件），若X表示取得次品的次数，则 （ ） 13 4 7 3 A．8 B．14 C．5 D．8 3 8．（2020·山西运城 高二期末（理））经检测有一批产品合格率为4 ，现从这批产品中任取5件，设取得  P(k) k 合格产品的件数为 ，则 取得最大值时 的值为（ ） A．2 B．3 C．4 D．5 二、多选题9．（2020·江苏鼓楼 南京师大附中高二期末）甲、乙两人练习射击，命中目标的概率分别为0.5和0.4，且 互不影响，现甲、乙两人各射击一次，下列说法正确的是（ ） A．目标恰好被命中一次的概率为0.5+0.4 B．目标恰好被命中两次的概率为0.5×0.4 C．目标被命中的概率为0.5×0.6+0.5×0.4 D．目标被命中的概率为1－0.5×0.6 10．（2020·江苏泰州 高一期末）下列叙述正确的是（ ） A．某人射击1次，"射中7环”与"射中8环"是互斥事件 B．甲、乙两人各射击1次，"至少有1人射中目标“与"没有人射中目标"是对立事件 1 C．抛掷一枚硬币，连续出现4次正面向上，则第5次出现反面向上的概率大于2 1 D．抛掷一枚硬币4次，恰出现2次正面向上的概率为2 11．（2020·山东任城 济宁一中高二期中）如城镇小汽车的普及率为75%，即平均每100个家庭有75个家 庭拥有小汽车，若从如城镇中任意选出5个家庭，则下列结论成立的是( ) 243 A．这5个家庭均有小汽车的概率为1024 27 B．这5个家庭中，恰有三个家庭拥有小汽车的概率为64 C．这5个家庭平均有3.75个家庭拥有小汽车 81 D．这5个家庭中，四个家庭以上(含四个家庭)拥有小汽车的概率为128 12．（2020·江苏亭湖 盐城中学高二月考）设火箭发射失败的概率为0.01，若发射10次，其中失败的次数 为X ，则下列结论正确的是（ ） E(X)0.1 P(X k)0.01k 0.9910k A． B． V(X)0.99 P(X k)Ck 0.01k 0.9910k C． D． 10 三、填空题13．在含有3件次品的10件产品中，任取4件，X表示取到的次品数，则P(X＝2)＝________. 14．（2019·哈尔滨市第一中学校高二期中（理））李明参加中央电视台《同一首歌》大会的青年志愿者选 拔，在已知备选的10道题中，李明能答对其中的6道，规定考试从备选题中随机地抽出3题进行测试，至 少答对2题才能入选.则李明入选的概率为__________. 15．（2020·四川省遂宁市第二中学校高三其他（理））3月5日为“学雷锋纪念日”，某校将举行“弘扬雷锋 精神做全面发展一代新人”知识竞赛，某班现从6名女生和3名男生中选出5名学生参赛，要求每人回答一 个问题，答对得2分，答错得0分，已知6名女生中有2人不会答所有题目，只能得0分，其余4人可得2 1 分，3名男生每人得2分的概率均为2 ，现选择2名女生和3名男生，每人答一题，则该班所选队员得分 之和为6分的概率__________. 16．（2020·天津南开 高三一模）甲、乙两名枪手进行射击比赛，每人各射击三次，甲三次射击命中率均 4 7 3 为5 ；乙第一次射击的命中率为8 ，若第一次未射中，则乙进行第二次射击，射击的命中率为4 ，如果又 1 未中，则乙进行第三次射击，射击的命中率为2 ．乙若射中，则不再继续射击．则甲三次射击命中次数的 期望为_____，乙射中的概率为_____． 四、解答题 17．（2020·辽宁沈阳 高二期中）甲、乙、丙三位学生各自独立地解同一道题，已知甲做对该题的概率为 1 3，乙、丙做对该题的概率分别为m，n(mn)，且三位学生能否做对相互独立，设X 为这三位学生中 做对该题的人数，其分布列为： X 0 1 2 3 1 1 P a b 3 36 m，n （1）求 的值； （2）求X 的数学期望．18．（2020·青海西宁 高二期末（理））在10件产品中,有3件一等品，4件二等品，3件三等品．从这10 件产品中任取3件．求： （1）取出的3件产品中一等品件数X 的分布列； （2）取出的3件产品中一等品件数多于二等品件数的概率． 19．（2020·通榆县第一中学校高二期末（理））某工厂在试验阶段大量生产一种零件．这种零件有A、B 3 两项技术指标需要检测，设各项技术指标达标与否互不影响．若A项技术指标达标的概率为4 ，B项技术 8 指标达标的概率为9，按质量检验规定：两项技术指标都达标的零件为合格品． （1）一个零件经过检测至少一项技术指标达标的概率；   E （2）任意依次抽取该种零件4个，设 表示其中合格品的个数，求 分布列及 ． 20．（2020·长春市第一中学高二期中（理））从某小组的5名女生和4名男生中任选3人去参加一项公益 活动. 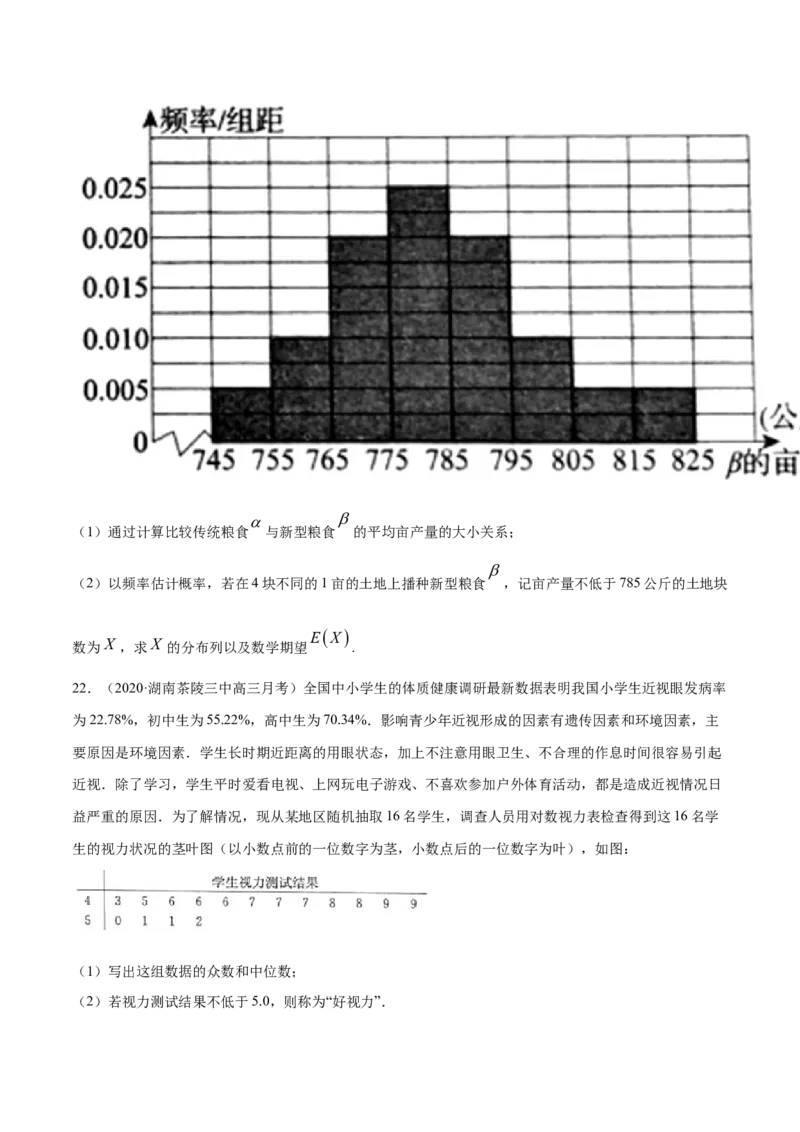(1)求所选3人中恰有一名男生的概率 (2)求所选3人中男生人数ξ的分布列及数学期望   21．（2020·全国高三其他（理））为了比较传统粮食 与新型粮食 的产量是否有差别，研究人员在若    干亩土地上分别种植了传统粮食 与新型粮食 ，并收集统计了 的亩产量，所得数据如下图所示.已知  传统粮食 的产量约为760公斤/亩.  （1）通过计算比较传统粮食 与新型粮食 的平均亩产量的大小关系；  （2）以频率估计概率，若在4块不同的1亩的土地上播种新型粮食 ，记亩产量不低于785公斤的土地块 EX 数为X ，求X 的分布列以及数学期望 . 22．（2020·湖南茶陵三中高三月考）全国中小学生的体质健康调研最新数据表明我国小学生近视眼发病率 为22.78%，初中生为55.22%，高中生为70.34%．影响青少年近视形成的因素有遗传因素和环境因素，主 要原因是环境因素．学生长时期近距离的用眼状态，加上不注意用眼卫生、不合理的作息时间很容易引起 近视．除了学习，学生平时爱看电视、上网玩电子游戏、不喜欢参加户外体育活动，都是造成近视情况日 益严重的原因．为了解情况，现从某地区随机抽取16名学生，调查人员用对数视力表检查得到这16名学 生的视力状况的茎叶图（以小数点前的一位数字为茎，小数点后的一位数字为叶），如图： （1）写出这组数据的众数和中位数； （2）若视力测试结果不低于5.0，则称为“好视力”．①从这16名学生中随机选取3名，求至少有2名学生是“好视力”的概率； ②以这16名学生中是“好视力”的频率代替该地区学生中是“好视力”的概率．若从该地区学生（人数较多） 中任选3名，记X 表示抽到“好视力”学生的人数，求X 的分布列及数学期望．