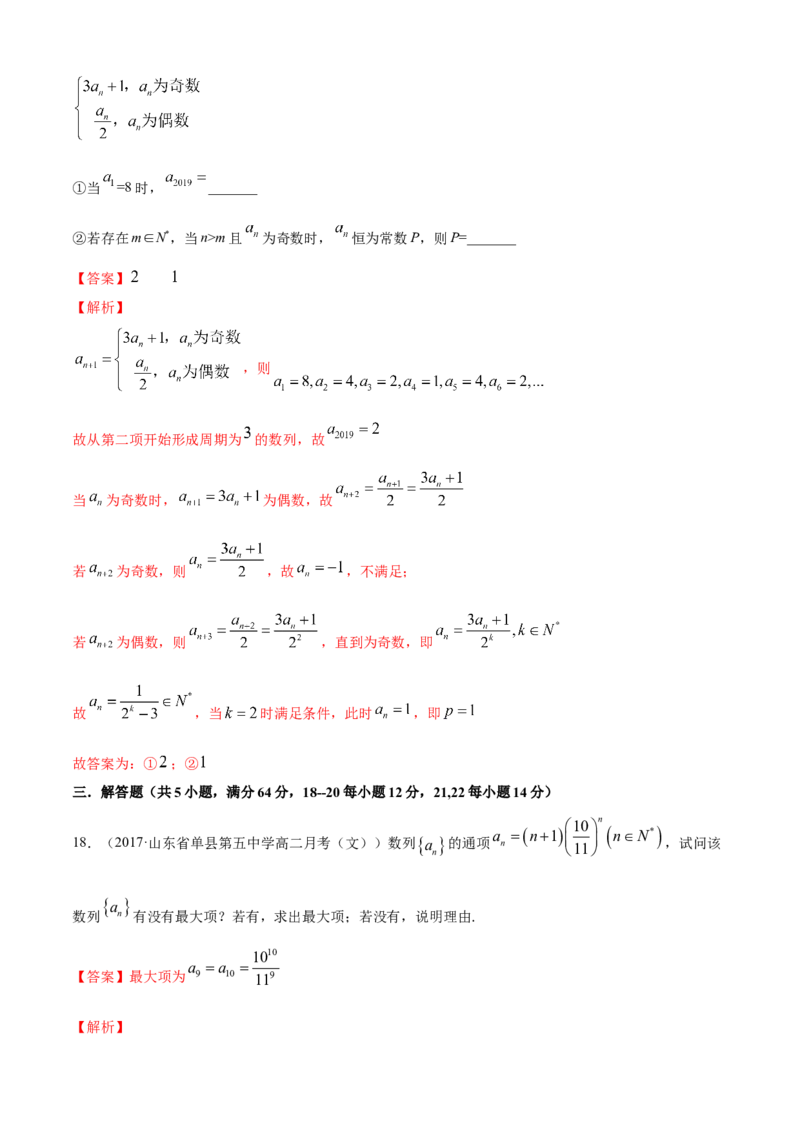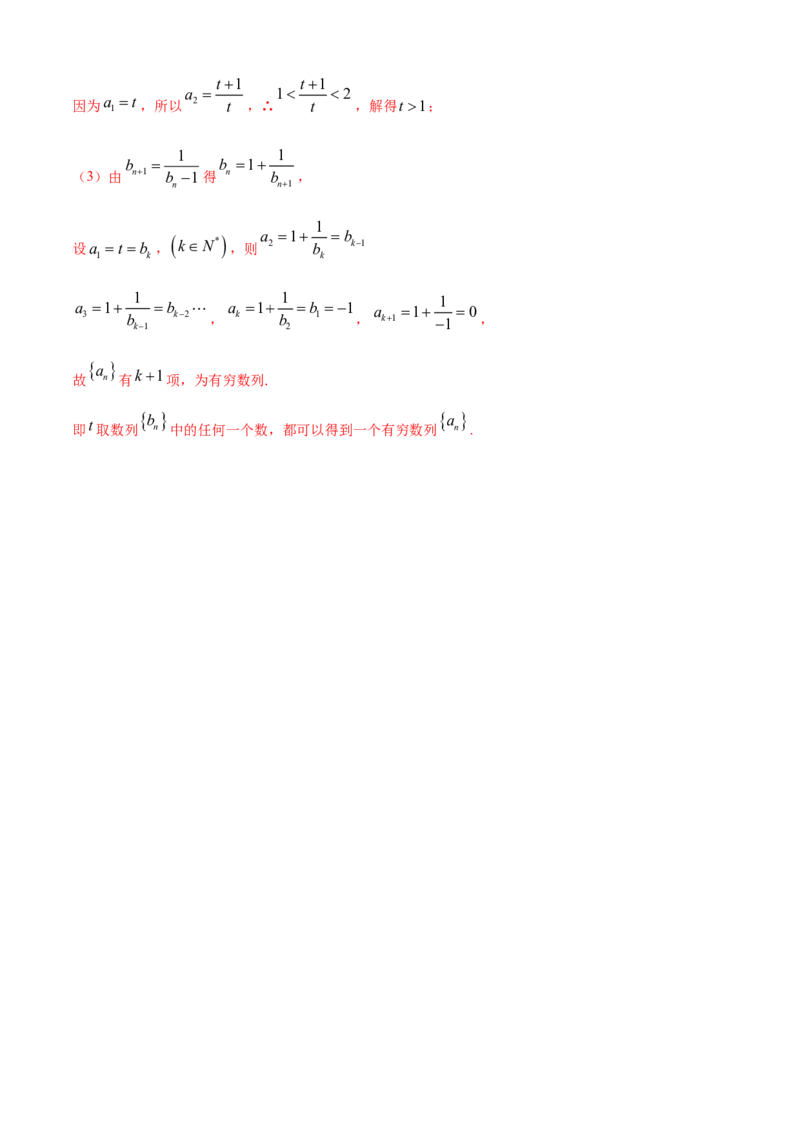专题4.1数列的概念（B卷提升篇）解析版_E015高中全科试卷_数学试题_选修2_01.同步练习_同步练习（第四套）_专题4.1数列的概念（B卷提升篇）

专题4.1数列的概念（B 卷提升篇）（人教A版第二册,浙江专用） 参考答案与试题解析 第Ⅰ卷（选择题） 一．选择题（共10小题，满分50分，每小题5分） 1．（2019·陕西省商丹高新学校期末（文））若数列 的通项公式为 ，则 （ ） A．27 B．21 C．15 D．13 【答案】A 【解析】 因为 ，所以 ， 故选：A. 2．（2019·黑龙江哈师大青冈实验中学开学考试）在数列 中， ， （ ， ），则 A． B． C．2 D．6 【答案】D 【解析】 ， （ ， ）， ， ，则 .3.（2019·绥德中学高二月考）数列 的通项公式 ，其前 项和为 ，则 A． B． C． D． 【答案】C 【解析】 根据三角函数的周期性可 ，同理得 ，可知周期为4， ． 4．（2020·四川凉山·期末（文））德国数学家科拉茨1937年提出了一个著名的猜想：任给一个正整数 ， 如果 是偶数，就将它减半（即 ）；如果 是奇数，则将它乘3加1（即 ），不断重复这样的运算， 经过有限步后，一定可以得到1．猜想的数列形式为： 为正整数，当 时， ，则数列 中必存在值为1的项．若 ，则 的值为（ ） A．1 B．2 C．3 D．4 【答案】B 【解析】 因为 ， ， 所以 ， ，， ， ， 故选：B 5．（2020·云南其他（理））数学上有很多著名的猜想，角谷猜想就是其中之一，它是指对于任意一个正 整数，如果是奇数，则乘3加1．如果是偶数，则除以2，得到的结果再按照上述规则重复处理，最终总能 够得到1．对任意正整数 ，记按照上述规则实施第 次运算的结果为 ，则使 的 所有 可能取值的个数为（ ） A．3 B．4 C．5 D．6 【答案】D 【解析】 由题意知 ， ， 由 ，得 ， ， 或 ． ①当 时， ， ， 或 ， 或 ． ②若 ，则 ， 或 ， 当 时， ，此时， 或 ， 当 时， ，此时， 或 ， 综上，满足条件的 的值共有6个． 故选：D． 6．（2020·贵州威宁·）观察数列21， ， ，24， ， ，27， ， ，…，则该数列的 第20项等于（ ）A．230 B．20 C． D． 【答案】C 【解析】 观察数列得出规律，数列中的项中， 指数、真数、弧度数是按正整数顺序排列， 且指数、对数、余弦值以3为循环， ， 可得第20项为 . 故选：C. 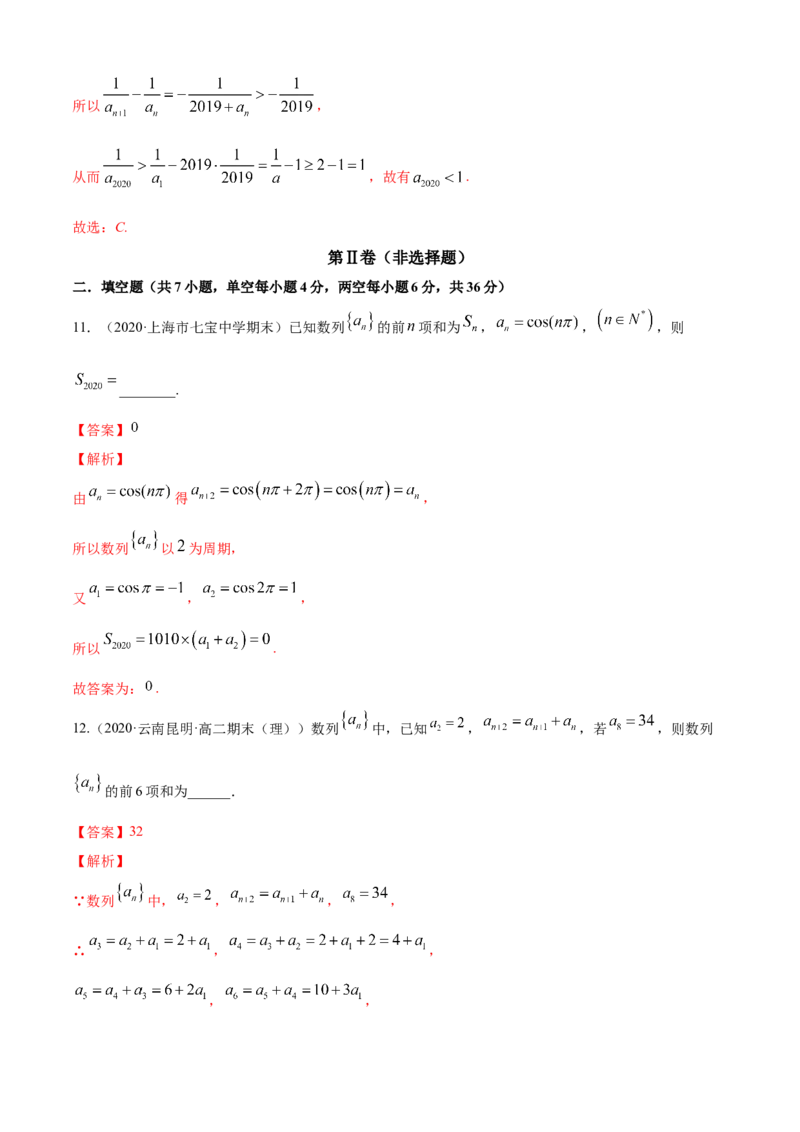7．（2020·邵东县第一中学月考）已知数列 满足： ，且数列 是 递增数列，则实数a的取值范围是（ ） A． B． C． D． 【答案】D 【解析】 根据题意，a＝f(n)＝ ，n∈N*，要使{a}是递增数列，必有 ，据 n n 此有： ，综上可得2m且 为奇数时， 恒为常数P，则P=_______ 【答案】 【解析】 ，则 故从第二项开始形成周期为 的数列，故 当 为奇数时， 为偶数，故 若 为奇数，则 ，故 ，不满足； 若 为偶数，则 ，直到为奇数，即 故 ，当 时满足条件，此时 ，即 故答案为：① ；② 三．解答题（共5小题，满分64分，18--20每小题12分，21,22每小题14分） n a n1 10  nN* 18．（2017·山东省单县第五中学高二月考（文））数列a 的通项 n  11   ，试问该 n a  数列 n 有没有最大项？若有，求出最大项；若没有，说明理由. 1010 a a  【答案】最大项为 9 10 119 【解析】a a n n1  设 a 是该数列的最大项，则  a a n n n1  10 n 10 n1  n1   n2    11 11 ∴ n n1  10 10 n1 n       11 11 9n10 解得 nN* ∵ ， n9或n10 ∴ ， 1010 a a  ∴最大项为 9 10 119 点睛：求数列最大项或最小项的方法 a a a a  n1 n(n2)  n1 n(n2) （1）可以利用不等式组 a a 找到数列的最大项；利用不等式 a a 找到数列的   n n1 n n1 最小项． （2）从函数的角度认识数列，注意数列的函数特征，利用函数的方法研究数列的最大项或最小项． a a a 1  2  n n2 n 19．（2020·黑龙江龙凤·大庆四中月考（文））数列 {a } 满足： 2 3 n1 ，nN*. n {a } （1）求 n 的通项公式； 1 9 b  S  （2）设 n a ，数列{b }的前n项和为S ，求满足 n 20 的最小正整数n. n n n a 2nn1 【答案】（1） n ；（2）10. 【解析】 a a a 1  2  n n2 n （1）∵ 2 3 n1 ． n=1时，可得a＝4， 1a a a 1  2  n1 n12 n1 n≥2时， 2 3 n ． a a a 1  2  n n2 n 与 2 3 n1 ． a n 两式相减可得n1＝（2n﹣1）+1=2n， a 2nn1 a 2nn1 ∴ n ．n=1时，也满足，∴ n . 1 1 11 1  b    （2） n a 2nn1=2  n n1   n 1 1 1 1 1 1  1 1  9   1        1  S  ∴S n 2 2 2 3 n n1 2 n1，又 n 20，可得n>9， 可得最小正整数n为10． a  a a a a a a  a a 1,nN* 20．（2020·上海市七宝中学期中）数列 n 满足 n n1 n2 n n1 n2 n n1 ，且   A0,0, a 1，a 2.规定的 a  通项公式只能用Asinxc   2  的形式表示. 1 2 n a （1）求 3的值； a  k  （2）证明3为数列 n 的一个周期，并用正整数 表示 ； a  （3）求 n 的通项公式. 2k 2 3 2    kN* a  sin  n  2 【答案】（1）a 3（2）证明见解析； 3 .（3） n 3  3 3  3 【解析】 （1）当a＝1，a＝2，aaa＝a+a+a，解得a＝3； 1 2 1 2 3 1 2 3 3 （2）当n＝2时，6a＝2+3+a，解得a＝1， 4 4 4 当n＝3时，3a＝1+3+a，解得a＝2， 5 5 5 …，可得a ＝a，当a＝1，a＝2，a＝3； n+3 n 1 2 3 故3为数列{a}的一个周期， n 2k 2k   kN* 则  ＝3，k N*，则 3 ； ∈ 2 （3）由（2）可得a＝Asin（ n+ ）+c， n 3 φ 2  则1＝Asin（ + ）+c，2＝﹣Asin（ + ）+c，3＝Asin +c， 3 3 φ φ φ 3 1 即1＝A• cos ﹣A• sin +c， 2 2 φ φ ① 3 1 2＝﹣A• cos ﹣A• sin +c， 2 2 φ φ ② 由 + ，可得3＝﹣Asin +2c， ∴①c＝2②，Asin ＝1， φ φ 3 ﹣ ，可得﹣1＝A• cos ， ① ② φ 3 则tan ＝﹣ ， φ  ∵| |＜ 2 ， φ  ∴ ＝﹣ ， 3 φ 2 3 ∴A＝﹣ 3 ， 2 3 2  a  sin n 2   故 n 3  3 3  ． {a } a 2 (n1)(a a )2(a n1) 21．（2020·湖北宜昌·其他（文））数列 n 中， 1 ， n1 n n . a a （1）求 2， 3的值；1 { } （2）已知数列{a }的通项公式是a n1，a n2 1，a n2 n中的一个，设数列 a 的前n项 n n n n n T n 360 和为S ，{a a }的前n项和为T ，若S ，求n的取值范围． n n1 n n n a 6 a 12 n17 n 【答案】（1） 2 ， 3 （2） ，且 是正整数 【解析】 n1a a 2a n1 （1）∵ n1 n n ， n3 a  a 2 ∴ n1 n1 n 13 a  a 26 ∴ 2 11 1 23 a  a 212 3 21 2 a  a n1 a n2 1 a n2 n a 6 a  （2）由数列 n 的通项公式是 n ， n ， n 中的一个，和 2 得数列 n 的 a n2 nnn1 通项公式是 n 1 1 1 1    由a nn1可得a nn1 n n1 n n 1 1 1  1 1 1 1 1  1     1      1         ∴a a a  2 2 3 n n1 n1 1 2 n 1 S 1 ∴ n n1 a a a a  a a a a a nn1 ∵ 2 1 3 2  n1 n n1 1， n a a a a  a a n2 3n ∴ 2 1 3 2  n1 n T n2 3n 即 nT n 360 由S ，得n2 4n3570，解得n17或n21 n n ∵ 是正整数， n n17 n ∴所求 的取值范围为 ，且 是正整数 1 a 1 22．（2020·上海市七宝中学期末）已知数列 a  满足a t， n1 a ，数列 a  可以是无穷数列， n 1 n n 3 5 1 1 t   也可以是有穷数列，如取t 1时，可得无穷数列：1，2，2 ，3，...；取 2 时，可得有穷数列： 2 ， 1，0. a 0 t （1）若 5 ，求 的值； 1a 2 n2 nN* t （2）若 n 对任意 ， 恒成立.求实数 的取值范围； 1 b   nN* （3）设数列 b  满足b 1， n1 b 1 ，求证：t取数列 b  中的任何一个数，都可以得 n 1 n n a  到一个有穷数列 n . 3 t  【答案】（1） 5；（2）t 1；（3）证明见解析. 【解析】 1 1 a 1 a  （1）由 n1 a 得 n a 1， n n1 1 2 1 3 a   t a   1 1 1 2 1 3 1 2 5 ∴a   1，a    ，  1 ，  1 ； 4 01 3 11 2 2 3 1 1 3 1  1 a 1 2 （2）若1a 2  n2,nN* ，则2 a ，2 n1 a ， n n n 1a 2 1a 2 即 n1 ，故只要 2 即可，t1 t1 a  1 2 因为 a t ，所以 2 t ，∴ t ，解得t 1； 1 1 1 b  b 1 （3）由 n1 b 1得 n b ， n n1 1 设a t b ，  kN* ，则 a 2 1 b b k1 1 k k 1 1 1 a 3 1 b b k2 ， a k 1 b b 1 1 ， a k1 1 1 0 ， k1 2 a  k1 故 n 有 项，为有穷数列. b  a  t 即 取数列 n 中的任何一个数，都可以得到一个有穷数列 n .