专题5.1导数的概念及其意义、导数的运算（B卷提升篇）原卷版_E015高中全科试卷_数学试题_选修2_01.同步练习_同步练习（第四套）

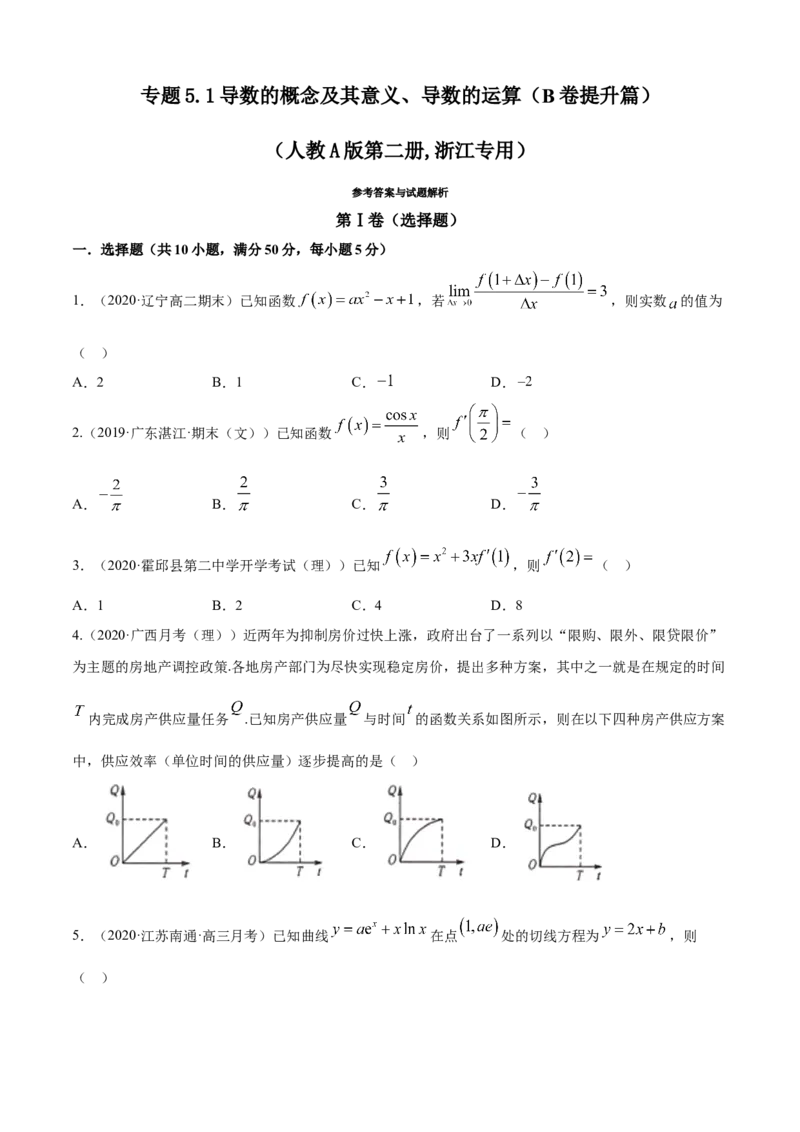
专题5.1导数的概念及其意义、导数的运算（B 卷提升篇） （人教A版第二册,浙江专用） 参考答案与试题解析 第Ⅰ卷（选择题） 一．选择题（共10小题，满分50分，每小题5分） 1．（2020·辽宁高二期末）已知函数 ，若 ，则实数 的值为 （ ） A．2 B．1 C． D． 2.（2019·广东湛江·期末（文））已知函数 ，则 （ ） A． B． C． D． 3．（2020·霍邱县第二中学开学考试（理））已知 ，则 （ ） A．1 B．2 C．4 D．8 4.（2020·广西月考（理））近两年为抑制房价过快上涨，政府出台了一系列以“限购、限外、限贷限价” 为主题的房地产调控政策.各地房产部门为尽快实现稳定房价，提出多种方案，其中之一就是在规定的时间 内完成房产供应量任务 .已知房产供应量 与时间 的函数关系如图所示，则在以下四种房产供应方案 中，供应效率（单位时间的供应量）逐步提高的是（ ） A． B． C． D． 5．（2020·江苏南通·高三月考）已知曲线 在点 处的切线方程为 ，则 （ ）A． B． C． D． 6．（2020·陕西省丹凤中学一模（理））点P在曲线 上移动，设点P处切线的倾斜角为 ， 则角 的范围是（ ） A． B． C． D． 7．（2020·霍邱县第二中学开学考试）若曲线 在 处的切线与直线 互相 垂直，则实数 等于（ ） A．-2 B．-1 C．1 D．2 8．（2019·江西修水·期末（理））已知过点P作曲线y＝x3的切线有且仅有两条，则点P的坐标可能是( ) A．(0,1) B．(0,0) C．(1,1) D．(－2，－1) 9．（2020·河北衡水·月考（理））已知M为抛物线 上一点，C在点M处的切线 交C的准线于点P，过点P向C再作另一条切线 ，则 的方程为（ ） A． B． C． D． 10．（2020·江苏省江浦高级中学月考）直线 是曲线 和曲线 的公切线，则 （ ） A． B． C． D． 第Ⅱ 卷（非选择题）二．填空题（共7小题，单空每小题4分，两空每小题6分，共36分） 11．（2020·岳麓·湖南师大附中月考）已知函数 ，若曲线 在 处的切 线与直线 平行，则 ______. 12.（2020·全国月考）已知函数 ，则在曲线 的所有切线中，斜率的最 大值为______. y 4asinxcosx (0,1) y  x1 13．（2020·甘肃省高三二模（文））已知曲线 在点 处的切线方程为 ，  tan(a ) 则 6 ______． 14．（2019·浙江西湖·学军中学高二期中）过原点作曲线 的切线，则切点的坐标为______，切线的 斜率为______． 15.（2020·山东省青岛市二模）已知函数 （ 为自然对数的底数）的图象恒 过定点 ， （1）则点 的坐标为__________； （2）若 在点 处的切线方程 ，则 __________. 16．（2020·宁波市北仑中学高二期中）设曲线 在点 处的切线 与曲线 上点 处 的切线垂直，则直线 的方程为________， 的坐标为________. 17．（2020·湖南天心·长郡中学月考（文））已知曲线 ： ，曲线 ： ， （1）若曲线 在 处的切线与 在 处的切线平行，则实数 ________；（2）若曲线 上任意一点处的切线为 ，总存在 上一点处的切线 ，使得 ，则实数 的取值范 围为________. 三．解答题（共5小题，满分64分，18--20每小题12分，21,22每小题14分） 18.( 2020·吉林蛟河一中月考（文））已知函数 （Ⅰ）求这个函数的导数 ； （Ⅱ）求这个函数在 处的切线方程. 19．（2020·广西钦州·高二期末（文））函数 在点 处的切线为 ． （1）若 与直线 平行，求实数 的值； （2）若 与直线 垂直，求实数 的值． 20．（2020·全国高一课时练习）比较函数 与 在区间 上的平均变 化率的大小. 21．（2020·江苏张家港·高二期中）已知 ，函数 的导函数为 ． （1）若 ，求曲线 在点 处的切线方程； （2）求 的值． 22．（2020·吉林蛟河一中月考（理））已知函数 ． （1）求 ； （2）求曲线 过点 的切线的方程．