2023~2024学年度第二学期期末考试高一数学参考答案及评分标准_2024-2025高一（7-7月题库）_2024年7月试卷_0710辽宁省锦州市2023-2024学年高一下学期期末考试

2023~2024学年度第二学期期末考试 高 一 数 学（参考答案与评分标准） 一、选择题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项 是符合题目要求的. ACDD BCBD 二、选择题：本题共3小题，每小题6分，共18分。在每小题给出的选项中，有多项符合 题目要求。全部选对的得6分，部分选对的得部分分，有选错的得0分。 9．BCD 10. AC 11．AD 三、填空题：本题共3小题，每小题5分，共15分。 6 12． 5 1 13． 2 14．(2−√ 3,√ 2−1) 四、解答题：本题共5小题，共77分。解答应写出文字说明、证明过程或演算步骤。 15．（本题满分13分）  2 解：（1）a在b上的投影的数量为：a cos  2 1 ⋯ ⋯ ⋯⋯ ⋯ ⋯ ⋯ ⋯4 分 4 2  （2）因为向量a，b的夹角为 ，且 a  2 ， b 3， 4  2 所以ab a  b cos  23 3． ⋯ ⋯ ⋯⋯⋯ ⋯ ⋯ ⋯ ⋯⋯ ⋯ ⋯ ⋯ ⋯6 分 4 2 2 所以a(ab)a ab231． ⋯ ⋯ ⋯⋯⋯ ⋯ ⋯ ⋯ ⋯⋯ ⋯ ⋯ ⋯ ⋯8 分 2  2 2 2  2 （3）2ab  2ab 4a 4abb 4 2 4395， ⋯ ⋯ ⋯ ⋯12分 所以 2ab  5． ⋯ ⋯ ⋯⋯⋯ ⋯ ⋯ ⋯ ⋯⋯ ⋯ ⋯ ⋯ ⋯⋯ ⋯ ⋯ ⋯ ⋯13 分 16.（本题满分15分） (1)证明：连接𝐴 𝐶，交𝐴𝐶 于点𝑂，连接𝑂𝐷， ⋯⋯ ⋯ ⋯ ⋯ ⋯2 分 1 1 因为四边形𝐴𝐶𝐶 𝐴 为平行四边形，所以𝑂为𝐴 𝐶中点，又𝐷为𝐵𝐶中点， 1 1 1 所以𝐷𝑂//𝐴 𝐵， ⋯ ⋯ ⋯ ⋯ ⋯⋯ ⋯ ⋯ ⋯⋯⋯⋯ ⋯ ⋯ ⋯ ⋯ ⋯ ⋯3 分 1 又𝐴 𝐵 ⊄平面𝐴𝐶 𝐷，𝐷𝑂 ⊂平面𝐴𝐶 𝐷， ⋯⋯⋯⋯ ⋯ ⋯ ⋯ ⋯ ⋯ ⋯4 分 1 1 1 1 {#{QQABIY4QggCgApAAAAgCEQFICgOQkAGAAYgOQEAMIAIAQAFABAA=}#}所以𝐴 𝐵//平面𝐴𝐶 𝐷. ⋯ ⋯ ⋯ ⋯⋯ ⋯ ⋯ ⋯⋯ ⋯ ⋯ ⋯ ⋯⋯ ⋯ ⋯ ⋯⋯ ⋯ ⋯ ⋯5 分 1 1 (2)解：设𝐴 到平面𝐴𝐶 𝐷的距离为𝑑， 1 1 因为𝐴𝐶 ⊥𝐴 𝐵，𝐷𝑂//𝐴 𝐵，所以𝐴𝐶 ⊥𝐷𝑂，又𝑂为𝐴𝐶 中点，所以𝐴𝐷 =𝐷𝐶 ， 1 1 1 1 1 1 因为△𝐴𝐵𝐶为等边三角形，所以𝐴𝐷 =√ 𝐴𝐵2−𝐵𝐷2 =√ 22−12 =√ 3 ， 所以𝐷𝐶 =√ C𝐶 2+12 =√ 3，所以C𝐶 =√ 2， ⋯⋯ ⋯ ⋯ ⋯ ⋯ ⋯ ⋯⋯ ⋯ ⋯ ⋯ ⋯7 分 1 1 1 𝑆 = 1 ×𝑂𝐷×𝐴𝐶 = 1 × √ 6 ×√ 6= 3， ⋯⋯ ⋯ ⋯⋯ ⋯ ⋯⋯ ⋯ ⋯⋯ ⋯ ⋯ ⋯8 分 △𝐴𝐷𝐶1 2 1 2 2 2 因为𝑉 = 1 𝑉 = 1 × 1 × 1 ×2×√ 2×√ 3= √ 6， 𝐷−𝐴𝐴1𝐶1 2 𝐵−𝐴𝐴1𝐶1 2 3 2 6 所以𝑉 =𝑉 = √ 6，所以 1 𝑆 ⋅𝑑 = √ 6，即 1 𝑑 = √ 6， 𝐴1−𝐴𝐶1𝐷 𝐷−𝐴𝐴1𝐶1 6 3 △𝐴𝐶1𝐷 6 2 6 解得𝑑 = √ 6， 3 即𝐴 到平面𝐴𝐶 𝐷的距离为√ 6． ⋯ ⋯⋯⋯ ⋯ ⋯ ⋯⋯ ⋯ ⋯ ⋯ ⋯ ⋯ ⋯⋯ ⋯ ⋯ ⋯ ⋯10 分 1 1 3 （3）解：由已知正三棱柱𝐴𝐵𝐶−𝐴 𝐵 𝐶 中，𝐷, 𝐸分别是𝐵𝐶，𝐵 B中点， 1 1 1 1 所以𝐶𝐶 ⊥面𝐴𝐵𝐶，所以 𝐶𝐶 ⊥𝐴𝐷,𝐴𝐷 ⊥𝐵𝐶，又𝐵𝐶∩𝐶𝐶 =𝐶， 1 1 1 所以𝐴𝐷 ⊥面𝐵𝐵 𝐶,𝐶，所以 𝐴𝐷 ⊥𝐶 𝐷,𝐴𝐷 ⊥𝐸𝐷， 1 1 所以∠𝐶 𝐷𝐸为二面角𝐶 −𝐷A− 𝐸的平面角. ⋯⋯ ⋯ ⋯ ⋯⋯ ⋯ ⋯ ⋯ ⋯ ⋯ ⋯ ⋯ ⋯12分 1 1 连接𝐶 𝐸 ,在△𝐵𝐷𝐸中 ，𝐷𝐸 =√𝐵𝐷2+𝐵𝐸2 =√1+ 1 = √6 1 2 2 在△𝐵 𝐶 𝐸中，𝐶 𝐸 =√𝐵 𝐶2+𝐵 𝐵2 =√4+ 1 = 3√2 1 1 1 1 1 1 2 2 由（2）知𝐷𝐶 =√3，所以𝐷𝐸2+𝐷𝐶2 =𝐶 𝐸2 ⋯ ⋯⋯⋯ ⋯ ⋯ ⋯⋯ ⋯ ⋯ ⋯ ⋯⋯ ⋯14 分 1 1 1 所以 𝐶 𝐷 ⊥𝐷𝐸， 1 所以二面角𝐶 −𝐷A− 𝐸的大小为90∘. ⋯ ⋯⋯ ⋯ ⋯⋯⋯ ⋯ ⋯ ⋯⋯ ⋯ ⋯ ⋯ ⋯⋯ ⋯15 分 1 17.（本题满分15分） 解：（1） f x2sinsinxcosx2cossin2xcos sin2xsincos（2sin2x1） sin2xsincos2xcos cos2x ⋯ ⋯⋯ ⋯ ⋯ ⋯⋯ ⋯ ⋯ ⋯ ⋯⋯ ⋯⋯ ⋯ ⋯ ⋯ ⋯⋯ ⋯ ⋯ ⋯2 分 2 {#{QQABIY4QggCgApAAAAgCEQFICgOQkAGAAYgOQEAMIAIAQAFABAA=}#}由 f    π x    f x0知， f x的图像关于点   π ,0  对称，  6   12   π  π 2π 所以2  kπ,kZ，得 kπ,kZ．  12 2 3 π π 因为 ，所以 ， ⋯⋯ ⋯ ⋯ ⋯⋯ ⋯ ⋯ ⋯⋯ ⋯ ⋯ ⋯⋯ ⋯ ⋯ ⋯ ⋯⋯ ⋯4分 2 3  π 即函数 f xcos  2x ．⋯⋯ ⋯ ⋯ ⋯⋯ ⋯ ⋯ ⋯⋯ ⋯ ⋯ ⋯⋯ ⋯ ⋯ ⋯ ⋯⋯ 5分  3  π 2π （2）因为 f xcos  2x ，所以T  π ⋯ ⋯ ⋯⋯ ⋯ ⋯ ⋯⋯ ⋯ ⋯ ⋯ ⋯7分  3 2 π π 2π 由2kπ2x 2kππ，kZ得kπ+  xkπ ，kZ 3 6 3  π 2π 所以函数 f x的单调递增区间是  kπ+ ，kπ  ，kZ. 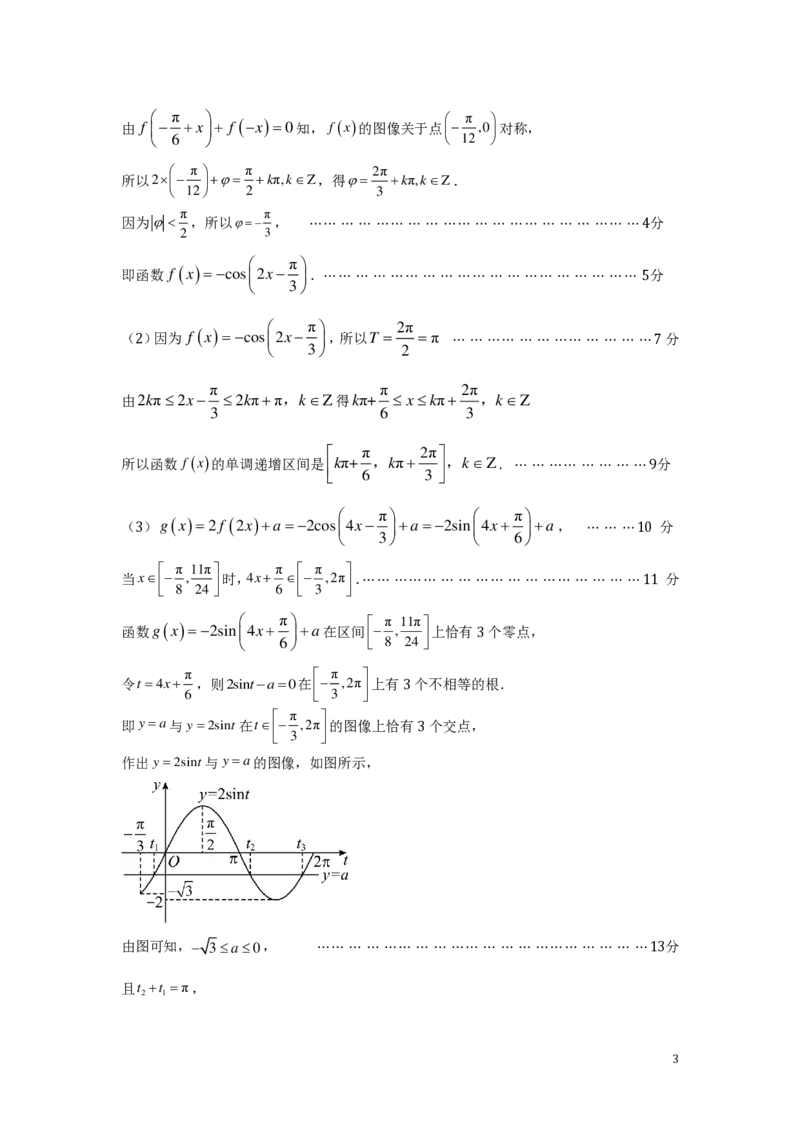⋯ ⋯ ⋯⋯ ⋯ ⋯ ⋯ ⋯9分  6 3   π  π （3）gx2f 2xa 2cos  4x  a 2sin  4x  a， ⋯ ⋯ ⋯10 分  3  6  π 11π π  π  当x   ,  时，4x    ,2π  ．⋯⋯ ⋯⋯⋯ ⋯ ⋯ ⋯⋯ ⋯ ⋯ ⋯⋯ ⋯ ⋯ ⋯ ⋯11 分  8 24  6  3   π  π 11π 函数gx2sin  4x  a在区间   ,  上恰有3个零点，  6  8 24  π  π  令t4x ，则2sinta0在   ,2π  上有3个不相等的根． 6  3   π  即ya与y2sint在t   ,2π  的图像上恰有3个交点，  3  作出y2sint与ya的图像，如图所示， 由图可知， 3a0， ⋯⋯ ⋯ ⋯ ⋯⋯ ⋯ ⋯ ⋯⋯ ⋯ ⋯ ⋯ ⋯⋯⋯ ⋯ ⋯ ⋯ ⋯13分 且t t π， 2 1 3 {#{QQABIY4QggCgApAAAAgCEQFICgOQkAGAAYgOQEAMIAIAQAFABAA=}#}1 π π π 1 所以sinx x sin t  t  sin  ． ⋯⋯ ⋯ ⋯ ⋯⋯ ⋯ ⋯ ⋯ ⋯15分 1 2 4 1 6 2 6 6 2 故a的取值范围为 3,0,sinx x 的值为 1 ．   1 2 2 评卷说明：（1）用余弦型函数解答，参考评分标准给分. （2）求a的取值范围时，如果答案正确但是没有必要的步骤说明减1分. 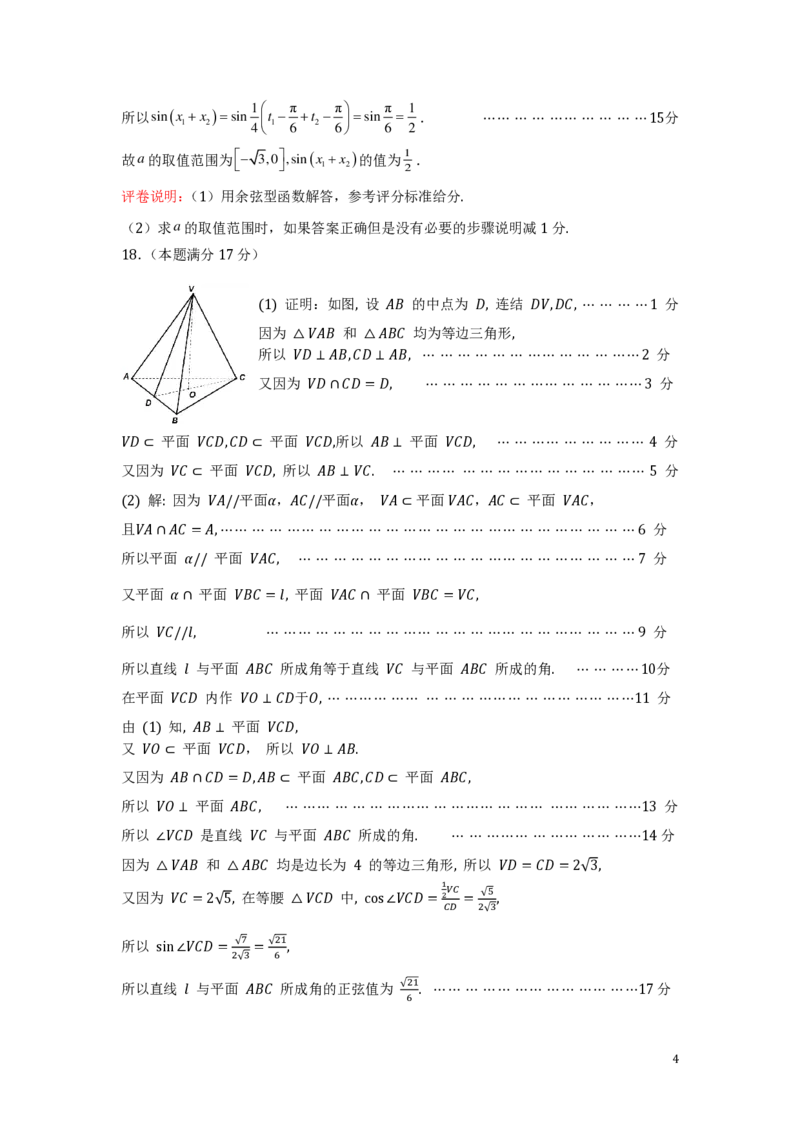18．（本题满分17分） (1) 证明：如图, 设 𝐴𝐵 的中点为 𝐷, 连结 𝐷𝑉,𝐷𝐶, ⋯ ⋯ ⋯ ⋯1 分 因为 △𝑉𝐴𝐵 和 △𝐴𝐵𝐶 均为等边三角形, 所以 𝑉𝐷 ⊥𝐴𝐵,𝐶𝐷 ⊥𝐴𝐵, ⋯ ⋯ ⋯ ⋯ ⋯ ⋯ ⋯⋯ ⋯ ⋯ ⋯ ⋯⋯2 分 又因为 𝑉𝐷∩𝐶𝐷 =𝐷, ⋯ ⋯ ⋯ ⋯ ⋯ ⋯ ⋯⋯ ⋯ ⋯ ⋯ ⋯⋯3 分 𝑉𝐷 ⊂ 平面 𝑉𝐶𝐷,𝐶𝐷 ⊂ 平面 𝑉𝐶𝐷,所以 𝐴𝐵 ⊥ 平面 𝑉𝐶𝐷, ⋯ ⋯ ⋯⋯ ⋯ ⋯ ⋯ ⋯⋯ 4 分 又因为 𝑉𝐶 ⊂ 平面 𝑉𝐶𝐷, 所以 𝐴𝐵 ⊥𝑉𝐶. ⋯ ⋯ ⋯⋯ ⋯ ⋯ ⋯ ⋯⋯ ⋯ ⋯ ⋯ ⋯ ⋯⋯ 5 分 (2) 解: 因为 𝑉𝐴//平面𝛼，𝐴𝐶//平面𝛼， 𝑉𝐴⊂平面 𝑉𝐴𝐶，𝐴𝐶 ⊂ 平面 𝑉𝐴𝐶， 且𝑉𝐴∩𝐴𝐶 =𝐴, ⋯⋯ ⋯ ⋯ ⋯⋯ ⋯ ⋯⋯ ⋯ ⋯ ⋯⋯ ⋯ ⋯ ⋯ ⋯⋯ ⋯ ⋯ ⋯⋯ ⋯ ⋯ ⋯ 6 分 所以平面 𝛼// 平面 𝑉𝐴𝐶, ⋯ ⋯ ⋯ ⋯ ⋯ ⋯ ⋯⋯ ⋯ ⋯ ⋯ ⋯⋯ ⋯ ⋯ ⋯⋯ ⋯ ⋯ ⋯ 7 分 又平面 𝛼∩ 平面 𝑉𝐵𝐶 =𝑙, 平面 𝑉𝐴𝐶∩ 平面 𝑉𝐵𝐶 =𝑉𝐶, 所以 𝑉𝐶//𝑙, ⋯ ⋯⋯ ⋯ ⋯ ⋯ ⋯ ⋯ ⋯⋯ ⋯ ⋯ ⋯ ⋯⋯ ⋯ ⋯ ⋯⋯ ⋯ ⋯ ⋯ 9 分 所以直线 𝑙 与平面 𝐴𝐵𝐶 所成角等于直线 𝑉𝐶 与平面 𝐴𝐵𝐶 所成的角. ⋯ ⋯ ⋯⋯10分 在平面 𝑉𝐶𝐷 内作 𝑉𝑂 ⊥𝐶𝐷于𝑂, ⋯ ⋯⋯⋯ ⋯⋯ ⋯ ⋯ ⋯ ⋯⋯⋯ ⋯ ⋯⋯ ⋯⋯ ⋯⋯11 分 由 (1) 知, 𝐴𝐵 ⊥ 平面 𝑉𝐶𝐷, 又 𝑉𝑂 ⊂ 平面 𝑉𝐶𝐷， 所以 𝑉𝑂 ⊥𝐴𝐵. 又因为 𝐴𝐵∩𝐶𝐷 =𝐷,𝐴𝐵 ⊂ 平面 𝐴𝐵𝐶,𝐶𝐷 ⊂ 平面 𝐴𝐵𝐶, 所以 𝑉𝑂 ⊥ 平面 𝐴𝐵𝐶, ⋯ ⋯⋯ ⋯ ⋯ ⋯ ⋯⋯⋯ ⋯ ⋯⋯⋯ ⋯ ⋯⋯ ⋯⋯ ⋯⋯ ⋯⋯13 分 所以 ∠𝑉𝐶𝐷 是直线 𝑉𝐶 与平面 𝐴𝐵𝐶 所成的角. ⋯ ⋯ ⋯⋯⋯ ⋯ ⋯⋯ ⋯⋯ ⋯⋯14分 因为 △𝑉𝐴𝐵 和 △𝐴𝐵𝐶 均是边长为 4 的等边三角形, 所以 𝑉𝐷 =𝐶𝐷 =2√3, 1 又因为 𝑉𝐶 =2√5, 在等腰 △𝑉𝐶𝐷 中, cos ∠𝑉𝐶𝐷 =2 𝑉𝐶 = √5 , 𝐶𝐷 2√3 所以 sin ∠𝑉𝐶𝐷 = √7 = √21 , 2√3 6 所以直线 𝑙 与平面 𝐴𝐵𝐶 所成角的正弦值为 √21 . ⋯⋯ ⋯ ⋯⋯ ⋯⋯ ⋯⋯ ⋯⋯ ⋯⋯17分 6 4 {#{QQABIY4QggCgApAAAAgCEQFICgOQkAGAAYgOQEAMIAIAQAFABAA=}#}19.（本题满分17分） 解：(1)在△𝐴𝐶𝐷中，由余弦定理有： 𝜋 𝐴𝐶2 =𝐴𝐷2+𝐶𝐷2−2𝐴𝐷⋅𝐶𝐷⋅cos𝛼 =1+4−2×1×2×cos =3， ⋯ ⋯ ⋯ ⋯ ⋯2 分 3 所以𝐴𝐶 =√ 3，所以𝐶𝐷2 =𝐴𝐷2+𝐴𝐶2,所以∠𝐷𝐴𝐶 =90∘，⋯⋯ ⋯ ⋯ ⋯⋯ ⋯ ⋯ ⋯ ⋯3 分 又因为△𝐴𝐵𝐶为等边三角形， 所以𝐴𝐵 =𝐴𝐶 =√ 3，且∠𝐵𝐴𝐷 =∠𝐵𝐴𝐶+∠𝐷𝐴𝐶 =150∘，⋯⋯ ⋯ ⋯ ⋯⋯ ⋯ ⋯ ⋯ ⋯4 分 所以𝑆 = 1 𝐴𝐵⋅𝐴𝐷⋅sin∠𝐵𝐴𝐷 = 1 ×√ 3×1×sin150𝑜 = √ 3 ⋯⋯ ⋯⋯ ⋯ ⋯ ⋯ ⋯6 分 △𝐴𝐵𝐷 2 2 4 (2)不妨设∠𝐷𝐴𝐶 =𝛽. 在△𝐴𝐶𝐷中，由余弦定理， 得𝐴𝐶2 =𝐴𝐷2+𝐶𝐷2−2𝐴𝐷⋅𝐶𝐷⋅cos𝛼 =1+4−2×2×cos𝛼 =5−4cos𝛼⋯ ⋯ ⋯8 分， 𝐴𝐶 2 +𝐴𝐷2−𝐷𝐶 2 5−4cos𝛼+1−4 1−2cos𝛼 cos𝛽 = = = . ⋯⋯ ⋯ ⋯ ⋯ ⋯10分 2𝐴𝐶⋅𝐴𝐷 2𝐴𝐶 𝐴𝐶 𝐴𝐶 𝐶𝐷 𝐴𝐶 2 在△𝐴𝐶𝐷中，由正弦定理， = ，即 = ， sin∠𝐴𝐷𝐶 sin∠𝐷𝐴𝐶 sin𝛼 sin𝛽 2sin𝛼 所以sin𝛽 = . ⋯ ⋯ ⋯ ⋯⋯ ⋯ ⋯ ⋯⋯ ⋯ ⋯⋯ ⋯ ⋯ ⋯⋯ ⋯ ⋯⋯⋯ ⋯ ⋯ ⋯ ⋯12 分 𝐴𝐶 所以𝑆 = 1 𝐴𝐵⋅𝐴𝐷⋅sin∠𝐵𝐴𝐷 = 1 𝐴𝐶⋅sin(𝛽+ 𝜋 )= 1 𝐴𝐶⋅( 1 sin𝛽+ √ 3 cos𝛽) △𝐴𝐵𝐷 2 2 3 2 2 2 1 √ 3 𝜋 √ 3 = sin𝛼+ (1−2cos𝛼)=sin(𝛼− )+ ， ⋯ ⋯ ⋯⋯ ⋯ ⋯ ⋯⋯ ⋯ ⋯ ⋯ ⋯⋯ ⋯14分 2 4 3 4 𝜋 𝜋 𝜋 2𝜋 又因为𝛼 ∈( ,𝜋)，所以𝛼− ∈( , )， 2 3 6 3 所以sin(𝛼− 𝜋 )+ √ 3 ∈( 1 ,1], ⋯ ⋯ ⋯⋯ ⋯ ⋯ ⋯⋯ ⋯ ⋯⋯ ⋯ ⋯ ⋯ ⋯ ⋯ ⋯⋯ ⋯16 分 3 4 2 即△𝐴𝐵𝐷的面积的取值范围为( 2+√ 3 , 4+√ 3 ]. ⋯ ⋯ ⋯⋯ ⋯ ⋯ ⋯⋯ ⋯ ⋯ ⋯ ⋯⋯ ⋯17 分 4 4 5 {#{QQABIY4QggCgApAAAAgCEQFICgOQkAGAAYgOQEAMIAIAQAFABAA=}#}