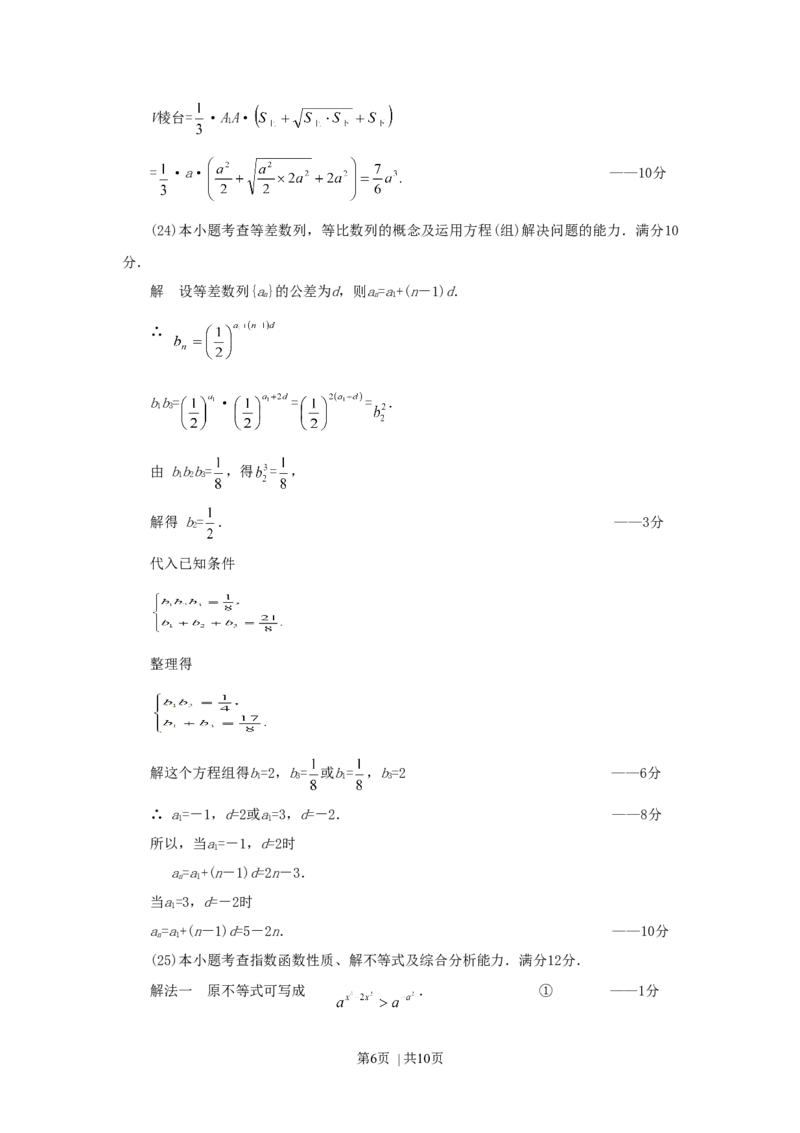文档内容
1991 年山东高考文科数学真题及答案
考生注意:这份试卷共三道大题(26个小题).满分120分.
一、选择题:本大题共15小题;每小题3分,共45分.在每小题给出的四个选项中,只有
一是符合题目要求的.把所选项前的字母填在题后括号内
王新奎新疆屯敞
(1) 已知sinα= ,并且α是第二象限的角,那么tgα的值等于 ( )
(A) (B) (C) (D)
(2) 焦点在(-1,0),顶点在(1,0)的抛物线方程是 ( )
(A) y2=8(x+1) (B) y2=-8(x+1)
(C) y2=8(x-1) (D) y2=-8(x-1)
(3) 函数y=cos4x-sin4x的最小正周期是 ( )
(A) (B) π (C) 2π (D) 4π
(4) P(2,5)关于直线x+y=0的对称点的坐标是 ( )
(A) (5,2) (B) (2,-5) (C) (-5,- (D) (-2,-
2) 5)
(5) 如果把两条异面直线看成“一对”,那么六棱锥的棱所在的12条直线中,异面直
线共有 ( )
(A) 12对 (B) 24对 (C) 36对 (D) 48对
(6) 函数y=sin(2x+ )的图像的一条对称轴的方程是 ( )
(A) x=- (B) x=-
(C) x= (D) x=
(7) 如果三棱锥S-ABC的底面是不等边三角形,侧面与底面所成的二面角都相等,且
顶点S在底面的射影O在△ABC内,那么O是△ABC的 ( )
(A) 垂心 (B) 重心 (C) 外心 (D) 内心
(8) 已知{a}是等比数列,且a>0,aa+2aa+aa=25,那么a+a的值等于( )
n n 2 4 3 5 4 6 3 5
(A) 5 (B) 10 (C) 15 (D) 20
第1页 | 共10页(9) 已知函数y= (x∈R,且x≠1),那么它的反函数为 ( )
(A) y= (x∈R,且x≠1)
(B) y= (x∈R,且x≠6)
(C) y= (x∈R,且x≠- )
(D) y= (x∈R,且x≠-5)
(10) 从4台甲型和5台乙型电视机中任意取出3台,其中至少要有甲型与乙型电视机各
1台,则不同的取法共有 ( )
(A) 140种 (B) 84种 (C) 70种 (D)35种
(11) 设甲、乙、丙是三个命题.如果甲是乙的必要条件;丙是乙的充分条件但不是
乙的必要条件,那么 ( )
(A) 丙是甲的充分条件,但不是甲的必要条件
(B) 丙是甲的必要条件,但不是甲的充分条件
(C) 丙是甲的充要条件
(D) 丙不是甲的充分条件,也不是甲的必要条件
(12) …(1- )]的值等于 ( )
(A) 0 (B) 1 (C) 2 (D) 3
(13) 如果AC<0且BC<0,那么直线Ax+By+C=0不通过 ( )
(A) 第一象限 (B) 第二象限 (C) 第三象限 (D) 第四象限
(14) 如果奇函数f(x)在区间[3,7]上是增函数且最小值为5,那么f(x)在区间[-7,
-3]上是 ( )
(A) 增函数且最小值为-5 (B) 增函数且最大值为-5
(C) 减函数且最小值为-5 (D) 减函数且最大值为-5
(15) 圆x2+2x+y2+4y-3=0上到直线x+y+1=0的距离为 的点共有 ( )
(A) 1个 (B) 2个 (C) 3个 (D) 4个
二、填空题:本大题共5小题;每小题3分,共15分.把答案填在题中横线上.
(16) 双曲线以直线x=-1和y=2为对称轴,如果它的一个焦点在y轴上,那么它的另一
第2页 | 共10页焦点的坐标是__________________.
(17) 已知sinx= ,则sin2(x- )=____________
王新奎新疆屯敞
(18) 不等式lg(x2+2x+2)<1的解集是_____________
王新奎新疆屯敞
(19) 在(ax+1)7的展开式中,x3的系数是x2的系数与x4的系数的等差中项,若实数
a>1,那么a=_____________
王新奎新疆屯敞
(20) 在长方体ABCD-ABCD中,已知顶点A上三条棱长分别是 、2.如果对
1 1 1 1
角线AC与过点A的相邻三个面所成的角分别是α、β、γ,那么cos2α+cos2β+
1
cos2γ=_________
王新奎新疆屯敞
三、解答题:本大题共6小题;共60分.
(21) (本小题满分8分)
求函数y=sin2x+2sinxcosx+3cos2x的最大值.
(22) (本小题满分8分)
已知复数z=1+i, 求复数 的模和辐角的主值.
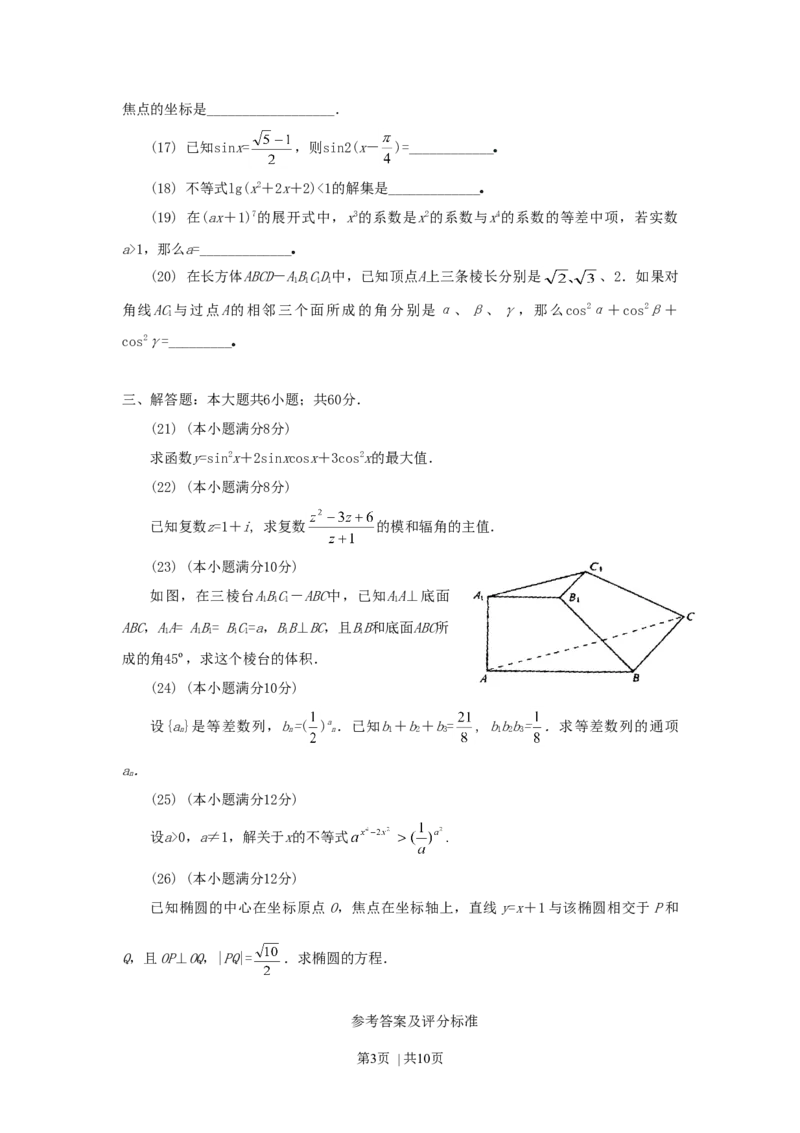
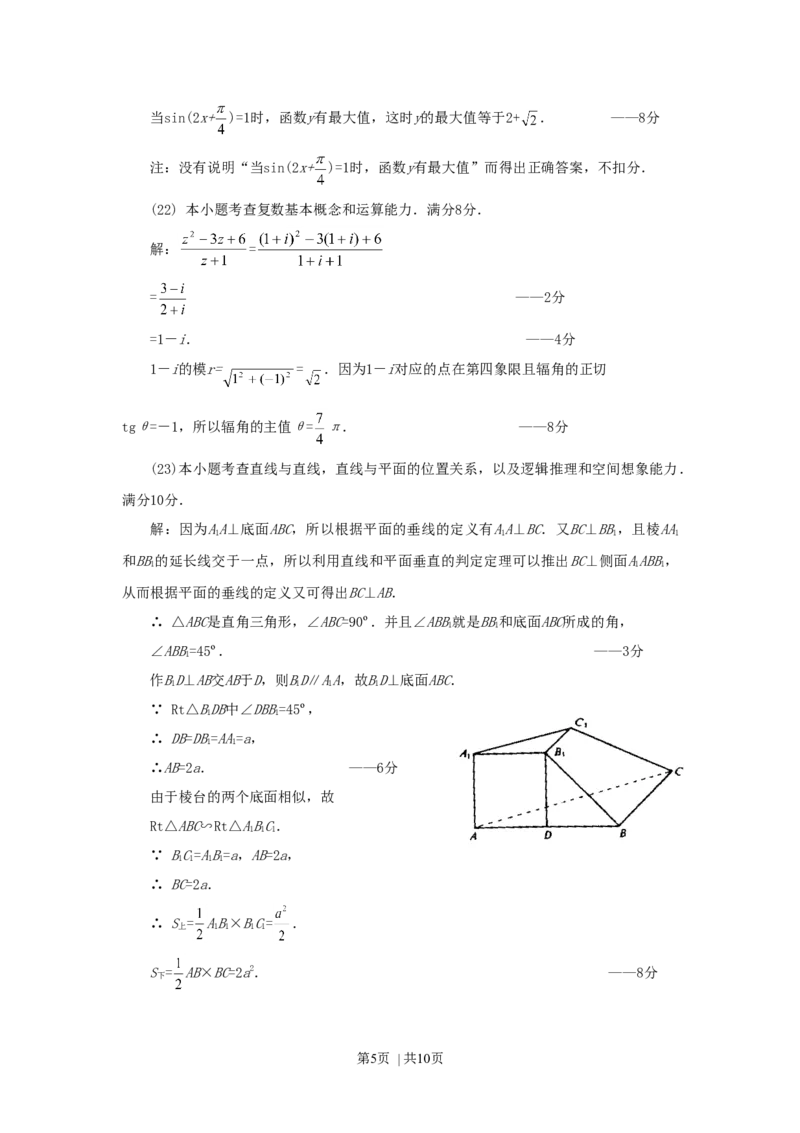
(23) (本小题满分10分)
如图,在三棱台ABC-ABC中,已知AA⊥底面
1 1 1 1
ABC,AA= AB= BC=a,BB⊥BC,且BB和底面ABC所
1 1 1 1 1 1 1
成的角45º,求这个棱台的体积.
(24) (本小题满分10分)
设{a}是等差数列,b=( )a.已知b+b+b= , bbb= .求等差数列的通项
n n n 1 2 3 1 2 3
a.
n
(25) (本小题满分12分)
设a>0,a≠1,解关于x的不等式
(26) (本小题满分12分)
已知椭圆的中心在坐标原点O,焦点在坐标轴上,直线y=x+1与该椭圆相交于P和
Q,且OP⊥OQ,|PQ|= .求椭圆的方程.
参考答案及评分标准
第3页 | 共10页说明:
一.本解答指出了每题所要考查的主要知识和能力,并给出了一种或几种较为常见的
解法,如果考生的解法与本解答不同,可根据试题的主要考查内容参照评分标准制定相应
评分细则.
二.每题都要评阅到底,不要因为考生的解答中出现错误而中断对该题的评阅.当考
生的解答在某一步出现错误,影响了后继部分时,如果该步以后的解答未改变这一题的内
容和难度时,可视影响的程度决定后面部分的给分,但不得超过后面部分应给分数的一半;
如果这一步以后的解答有较严重的错误,就不给分.
三.为了阅卷方便,本试题解答中的推导步骤写得较为详细,允许考生在解题过程中
合理省略非关键性的推导步骤.
四.解答右端所注分数,表示考生正确做到这一步应得的累加分数.
五.只给整数分数.
一.选择题.本题考查基本知识和基本运算.每小题3分,满分45分.
(1)A (2)D (3)B (4)C (5)B (6)A (7)D (8)A (9)B (10)C (11)A (12)C
(13)C (14)B (15)C
二.填空题.本题考查基本知识基本运算.每小题3分,满分15分.
(16) (-2,2) (17) 2- (18) {x|-40,
所以②式等价于
③
④
——5分
解③式得 x<- 或x> ,
解④式得 - 1时,由①式得
x4-2x2+a2>0, ⑤ ——9分
由于a>1,判别式△<0,故⑤式对任意实数x成立,即得原不等式的解集为
{x|-∞1时,原不等式的解集为
{x|-∞1时,由①式得
x4-2x2+a2>0, ⑧ ——9分
配方得 (x2-1)2+a2-1>0, ⑨
对任意实数x,不等式⑨都成立,即a>1时,原不等式的解集为
{x|-∞1时,原不等式的解集为 {x|-∞