文档内容
专题 09 预备知识九:函数的概念
1、学会运用集合语言表示函数,理解函数的定义及构成要素,会求解简单函数的定义域和值域
2、掌握函数相等与判定的方法
知识点一:函数的概念
1、初中学习的函数的传统定义
设在一个变化的过程中,有两个变量 和 ,如果给定了一个 值,相应地就有唯一确定的一个 值
与之对应,那么我们就称 是 的函数,其中 是自变量, 是因变量.它们描述的是两个变量之间的依赖
关系.
2、函数的近代定义
一般地,设 , 是非空的实数集,如果对于集合 中的任意一个数 ,按照某种确定的对应关系
,在集合 中都有唯一确定的数 和它对应,那么就称 为从集合 到集合 的一个函数
(function),记作 , .其中, 叫做自变量, 的取值范围 叫做函数的定义域;与 的值相
对应的 值叫做函数值,函数值的集合 叫做函数的值域.显然,值域是集合 的子集.
函数的四个特征:
①非空性: , 必须为非空数集(注意不仅非空,还要是数集),定义域或值域为空集的函数是不存在
的.
②任意性:即定义域中的每一个元素都有函数值.
③单值性:每一个自变量有且仅有唯一的函数值与之对应(可以多对一,不能一对多).
④方向性:函数是一个从定义域到值域的对应关系,如果改变这个对应方向,那么新的对应所确定
的关系就不一定是函数关系.
知识点二:函数的三要素
1、定义域:函数的定义域是自变量的取值范围.
2、对应关系:对应关系 是函数的核心,它是对自变量 实施“对应操作”的“程序”或者“方法”.
3、值域:与 的值相对应的 值叫做函数值,函数值的集合 叫做函数的值域(range).
知识点三:函数相等
同一函数:只有当两个函数的定义域和对应关系都分别相同时,这两个函数才相等,即是同一个函数.
知识点四:区间的概念
1区间的概念
设 , 是实数,且 ,满足 的实数 的全体,叫做闭区间,
学科网(北京)股份有限公司 学科网(北京)股份有限公司记作 ,即, 。如图: , 叫做区间的端点.在数轴上表示一个区间时,若
区间包括端点,则端点用实心点表示;若区间不包括端点,则端点用空心点表示.
集合
区间
2含有无穷大的表示
全体实数也可用区间表示为 ,符号“ ”读作“正无穷大”,“ ”读作“负无穷大”,即
。
集合
区间
对点特训一:函数关系的判断
典型例题
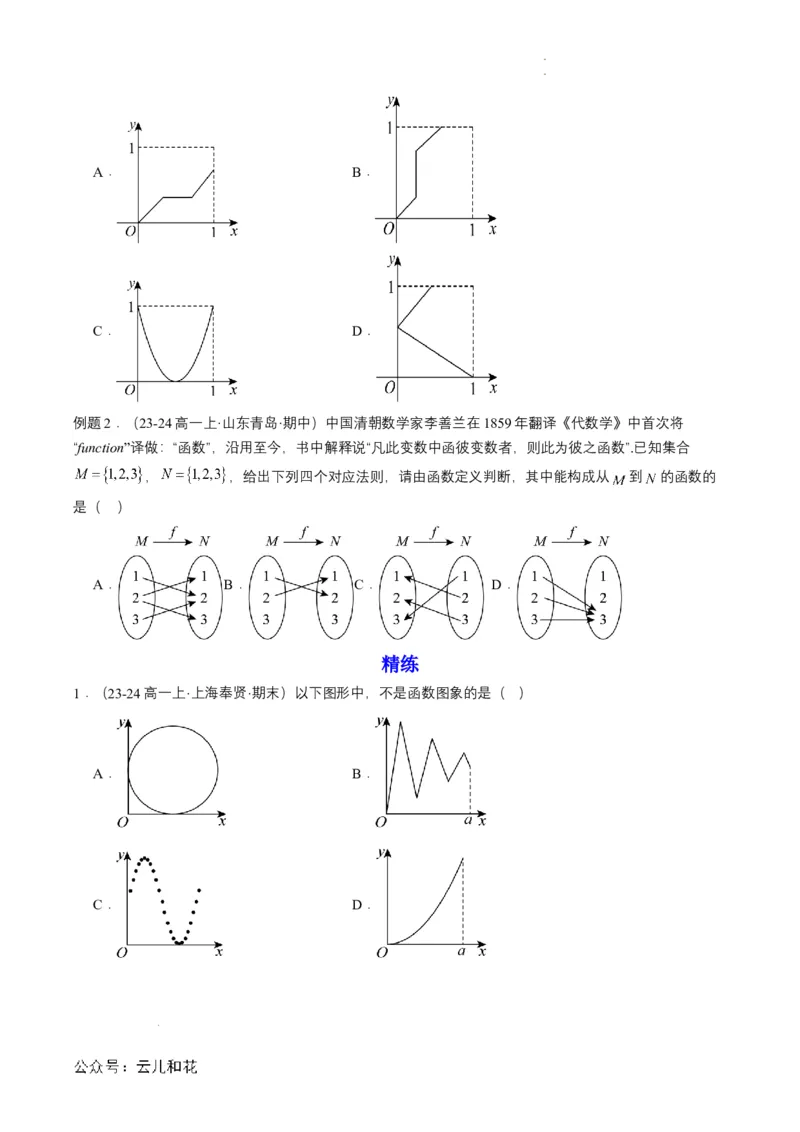
例题1.(23-24高一上·北京·期中)若函数 的定义域为 ,值域为 ,那么
函数 的图象可能是( )
学科网(北京)股份有限公司 学科网(北京)股份有限公司A. B.
C. D.
例题2.(23-24高一上·山东青岛·期中)中国清朝数学家李善兰在1859年翻译《代数学》中首次将
“function”译做:“函数”,沿用至今,书中解释说“凡此变数中函彼变数者,则此为彼之函数”.已知集合
, ,给出下列四个对应法则,请由函数定义判断,其中能构成从 到 的函数的
是( )
A. B. C. D.
精练
1.(23-24高一上·上海奉贤·期末)以下图形中,不是函数图象的是( )
A. B.
C. D.
学科网(北京)股份有限公司 学科网(北京)股份有限公司2.(多选)(22-23高一上·陕西西安·期末)设集合 ,则下列图象能表示
集合 到集合Q的函数关系的有( )
A. B.
C. D.
对点特训二:集合与区间的转化
典型例题
例题1.(23-24高一上·全国·课后作业)区间 表示的集合是( )
A. 或 B.
C. D.
例题2.(23-24高一上·河北石家庄·期中) 用区间表示为 ; 用区
间表示为 .
例题3.(23-24高一上·全国·课后作业)把下列数集用区间表示:
(1) ;
(2) ;
(3) ;
(4) 或 .
精练
学科网(北京)股份有限公司 学科网(北京)股份有限公司1.(23-24高一上·新疆阿克苏·阶段练习)下列叙述正确的是( )
A. 用区间可表示为 B. 用区间可表示为
C. 用集合可表示为 D. 用集合可表示为
2.(23-24高一上·重庆·期中)集合 用区间表示为( )
A. B.
C. D.
3.(23-24高一上·广东江门·期中)不等式 的解集用区间表达为 .
对点特训三:同一个函数
典型例题
例题1.(23-24高二下·福建三明·阶段练习)下列各组函数相等的是( )
A. , B. ,
C. , D. ,
例题2.(多选)(23-24高一上·浙江·期中)下列各组函数不是同一函数的是( )
A. B.
C. D.
精练
1.(多选)(23-24高一上·安徽马鞍山·阶段练习)下列各组函数表示同一函数的是( )
A. B.
C. D.
2.(多选)(23-24高一上·陕西宝鸡·期中)下列函数 与 表示同一函数的是( )
A. , B. ,
C. D.
学科网(北京)股份有限公司 学科网(北京)股份有限公司对点特训四:函数求值问题
典型例题
例题1.(23-24高一上·山西大同·阶段练习)已知函数 的对应关系如下表,函数 的图象
是如图的曲线 ,其中 ,则 的值为( )
1 2 3
2 3 0
A.3 B.2 C.1 D.0
例题2.(23-24高一上·山东济宁·阶段练习)已知 , .
(1)求 , 的值;
(2)求 , 的值.
精练
1.(23-24高一上·上海·阶段练习)已知 ,则 .
2.(23-24高一上·上海虹口·期末)若 表示不大于 的最大整数,比如 ,则
.
对点特训五:求函数的定义域
学科网(北京)股份有限公司 学科网(北京)股份有限公司典型例题
例题1.(23-24高一下·广东汕头·期中)函数 的定义域为( )
A.{ 且 } B.{ 且 }
C. D.{ 且 }
例题2.(22-23高一上·全国·期中)已知函数 的定义域是 ,则函数 的定义域是
( )
A. B. C. D.
例题3.(23-24高一上·湖南张家界·阶段练习)已知函数 ,则 的定义域为
精练
1.(23-24高一上·广东佛山·阶段练习)函数 的定义域为( )
A. B. C. D.
2.(23-24高一上·山东·期中)若函数 的定义域为 ,则函数 的定义域为( )
A. B. C. D.
3.(2024·湖北武汉·二模)已知函数 的定义域为 ,则函数 的定义域为
.
对点特训六:函数的值域
角度1:一次、二次、反比例函数的值域
典型例题
例题1.(23-24高一上·福建厦门·期中)已知函数 ,函数 的值域为( )
A. B. C. D.
例题2.(2023高一·全国·专题练习)求下列函数的值域:
(1) , ;
学科网(北京)股份有限公司 学科网(北京)股份有限公司(2) , ;
精练
1.(23-24高一上·湖南长沙·期中)函数 的值域为 .
2.(23-24高一上·北京·期中)函数 , 的值域为 .
角度2:根式型值域
典型例题
例题1.(2024高三·全国·专题练习)函数 的值域为 .
例题2.(22-23高一上·浙江·期中)函数 的值域是( )
A. B. C. D.
精练
1.(23-24高一上·安徽亳州·期中)函数 的值域为
2.(22-23高一上·湖北鄂州·期中)函数 的值域是( )
A. B. C. D.
角度3:分式型值域
典型例题
例题1.(23-24高一上·安徽合肥·期中)函数 的值域为( )
A. B. C. D.
例题2.(23-24高一上·全国·课后作业)函数 的值域是 .
学科网(北京)股份有限公司 学科网(北京)股份有限公司精练
1.(23-24高一上·重庆云阳·阶段练习)函数 的值域为( )
A. B. C. D.
2.(23-24高一上·江苏南京·期中)函数 的最大值为 .
一、单选题
1.(23-24高一上·安徽马鞍山·期中)下列各组函数中,表示同一个函数的是( )
A. B.
C. D.
2.(23-24高一上·北京·期中)函数 的定义域是( )
A. B.
C. D.
3.(23-24高一上·安徽蚌埠·期末)函数 的定义域为 ,则函数 的定义域为
( )
A. B. C. D.
4.(23-24高一上·湖北咸宁·阶段练习)对任意的 , 表示不超过x的最大整数,十八世纪,
被“数学王子”高斯采用,因此得名高斯函数,人们更习惯称之为“取整函数”,则
( )
A. B. C. D.
5.(23-24高一上·河南驻马店·阶段练习)函数 的值域为( )
A. B.
C. D.
6.(23-24高一上·河南·期中)若函数 的定义域为R,则实数a的取值范围是( )
学科网(北京)股份有限公司 学科网(北京)股份有限公司A. B.
C. D.
7.(23-24高三上·陕西汉中·阶段练习)已知函数 的定义域为R,则实数a的取值范围
为( )
A. B. 或
C. D. 或
8.(19-20高一上·安徽芜湖·阶段练习)在实数集 中定义一种运算“ ”,具有下列性质:
①对任意a, , ;
②对任意 , ;
③对任意a, , .
则函数 的值域是( )
A. B. C. D.
二、多选题
9.(23-24高一上·福建龙岩·阶段练习)下列各组函数是同一个函数的是( )
A. 与 B. 与
C. 与 D. 与
三、填空题
10.(23-24高一上·宁夏石嘴山·期中)函数 的值域为
四、解答题
11.(23-24高三上·天津河西·期中)已知函数 .
(1)当 时,求 的值域;
(2)若 的定义域为 ,求实数 的值;
(3)若 的定义域为 ,求实数 的取值范围.
学科网(北京)股份有限公司 学科网(北京)股份有限公司12.(23-24高一上·广东佛山·阶段练习)完成下列各小题:
(1)若正数 , 满足 ,求 的最小值.
(2)已知 ,求 的最小值.
(3)已知定义在 的函数 ,求函数的值域
学科网(北京)股份有限公司 学科网(北京)股份有限公司