文档内容
5.某市有15个旅游景点,经计算,黄金周期间各个景点的旅游人数平均为20万,标准差为s,后来经
(新教材)下学期高一期末备考金卷
核实,发现甲、乙两处景点统计的人数有误,甲景点实际为20万,被误统计为15万,乙景点实际为18
数 学 万,被误统计成23万;更正后重新计算,得到标准差为s,则s与s 的大小关系为( )
1 1
A.s=s B.ss D.不能确定
1 1 1
注意事项:
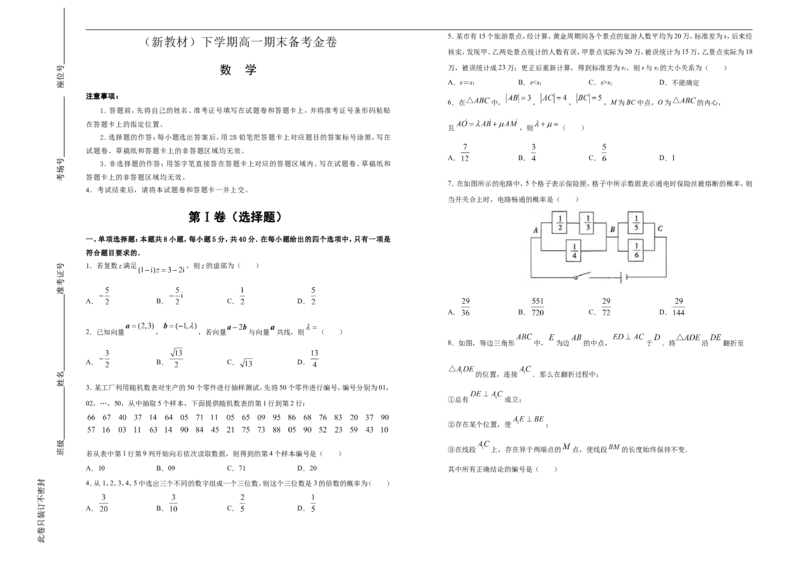
6.在 中, , , ,M为BC中点,O为 的内心,
1.答题前,先将自己的姓名、准考证号填写在试题卷和答题卡上,并将准考证号条形码粘贴
在答题卡上的指定位置。
且 ,则 ( )
2.选择题的作答:每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑,写在
试题卷、草稿纸和答题卡上的非答题区域均无效。
A. B. C. D.1
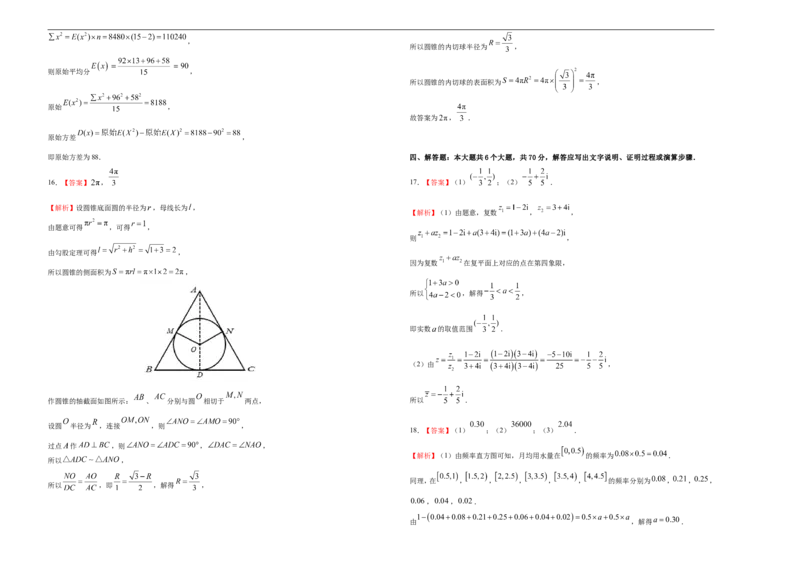
3.非选择题的作答:用签字笔直接答在答题卡上对应的答题区域内。写在试题卷、草稿纸和
答题卡上的非答题区域均无效。
7.在如图所示的电路中,5个格子表示保险匣,格子中所示数据表示通电时保险丝被熔断的概率,则
4.考试结束后,请将本试题卷和答题卡一并上交。
当开关合上时,电路畅通的概率是( )
第Ⅰ卷(选择题)
一、单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是
符合题目要求的.
1.若复数z满足 ,则z的虚部为( )
A. B. C. D.
A. B. C. D.
2.已知向量 , ,若向量 与向量 共线,则 ( )
8.如图,等边三角形 中, 为边 的中点, 于 .将 沿 翻折至
A. B. C. D.
的位置,连接 .那么在翻折过程中:
3.某工厂利用随机数表对生产的50个零件进行抽样测试,先将50个零件进行编号,编号分别为01,
①总有 成立;
02,…,50,从中抽取5个样本,下面提供随机数表的第1行到第2行:
②存在某个位置,使 ;
③在线段 上,存在异于两端点的 点,使线段 的长度始终保持不变.
若从表中第1行第9列开始向右依次读取数据,则得到的第4个样本编号是( )
A.10 B.09 C.71 D.20 其中所有正确结论的编号是( )
4.从1,2,3,4,5中选出三个不同的数字组成一个三位数,则这个三位数是3的倍数的概率为( )
A. B. C. D.
封封密密不不订订装装只只卷卷此此
号号位位座座
号号场场考考
号号证证考考准准
名名姓姓
级级班班C.若 ,则 D.若 ,则
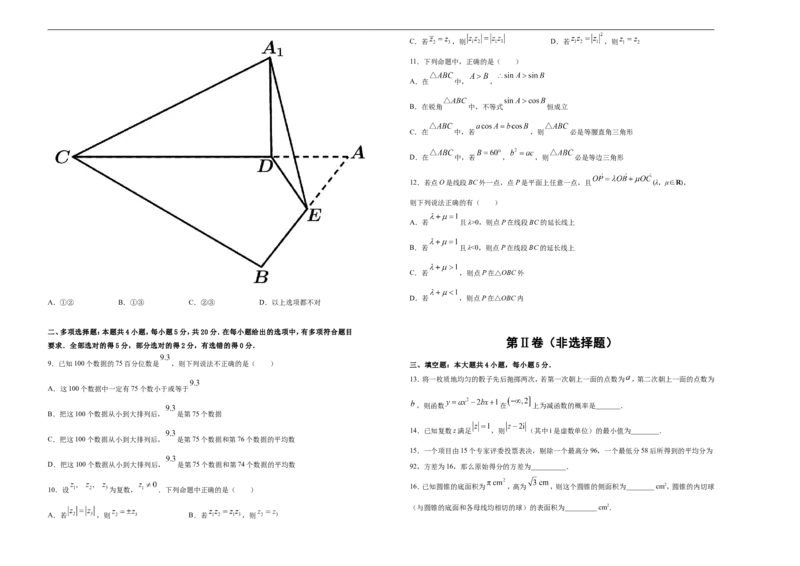
11.下列命题中,正确的是( )
A.在 中, ,
B.在锐角 中,不等式 恒成立
C.在 中,若 ,则 必是等腰直角三角形
D.在 中,若 , ,则 必是等边三角形
12.若点O是线段BC外一点,点P是平面上任意一点,且 (λ,μ∈R),
则下列说法正确的有( )
A.若 且λ>0,则点P在线段BC的延长线上
B.若 且λ<0,则点P在线段BC的延长线上
C.若 ,则点P在△OBC外
D.若 ,则点P在△OBC内
A.①② B.①③ C.②③ D.以上选项都不对
二、多项选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目
第Ⅱ卷(非选择题)
要求.全部选对的得5分,部分选对的得2分,有选错的得0分.
9.已知100个数据的75百分位数是 ,则下列说法不正确的是( ) 三、填空题:本大题共4小题,每小题5分.
13.将一枚质地均匀的骰子先后抛掷两次,若第一次朝上一面的点数为 ,第二次朝上一面的点数为
A.这100个数据中一定有75个数小于或等于
,则函数 在 上为减函数的概率是_______.
B.把这100个数据从小到大排列后, 是第75个数据
14.已知复数z满足 ,则 (其中i是虚数单位)的最小值为________.
C.把这100个数据从小到大排列后, 是第75个数据和第76个数据的平均数
15.一个项目由15个专家评委投票表决,剔除一个最高分96,一个最低分58后所得到的平均分为
D.把这100个数据从小到大排列后, 是第75个数据和第74个数据的平均数 92,方差为16,那么原始得分的方差为__________.
16.已知圆锥的底面积为 ,高为 ,则这个圆锥的侧面积为________ cm2,圆锥的内切球
10.设 为复数, .下列命题中正确的是( )
(与圆锥的底面和各母线均相切的球)的表面积为_________ cm2.
A.若 ,则 B.若 ,则四、解答题:本大题共6个大题,共70分,解答应写出文字说明、证明过程或演算步骤.
17.(10分)已知复数 , , 为虚数单位.
(1)若复数 ,在复平面上对应的点在第四象限,求实数a的取值范围;
(2)若 ,求 的共轭复数.
19.(12分)进行垃圾分类收集可以减少垃圾处理量和处理设备,降低处理成本,减少土地资源的消耗,
具有社会、经济、生态等多方面的效益,是关乎生态文明建设全局的大事.为了普及垃圾分类知识,某
学校举行了垃圾分类知识考试,试卷中只有两道题目,已知甲同学答对每题的概率都为 ,乙同学答
对每题的概率都为 ,且在考试中每人各题答题结果互不影响.已知每题甲,乙同时答对的
概率为 ,恰有一人答对的概率为 .
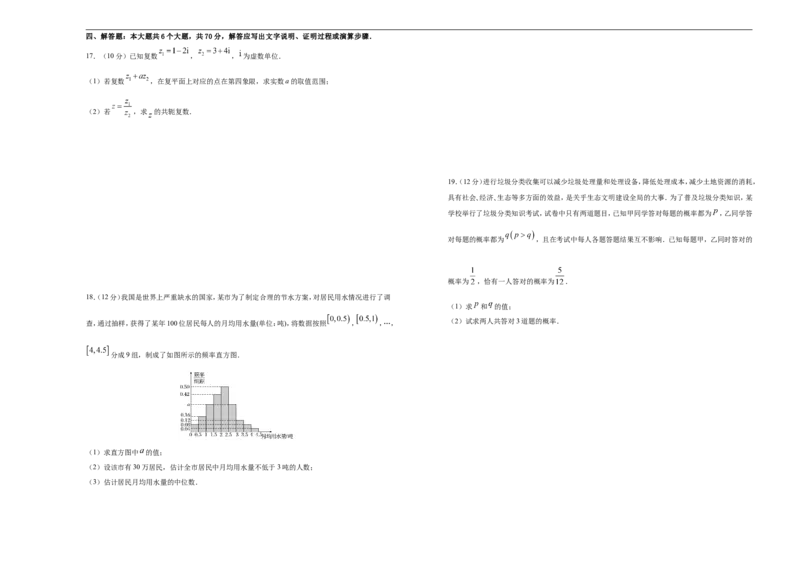
18.(12分)我国是世界上严重缺水的国家,某市为了制定合理的节水方案,对居民用水情况进行了调
(1)求 和 的值;
(2)试求两人共答对3道题的概率.
查,通过抽样,获得了某年100位居民每人的月均用水量(单位:吨),将数据按照 , ,…,
分成9组,制成了如图所示的频率直方图.
(1)求直方图中 的值;
(2)设该市有30万居民,估计全市居民中月均用水量不低于3吨的人数;
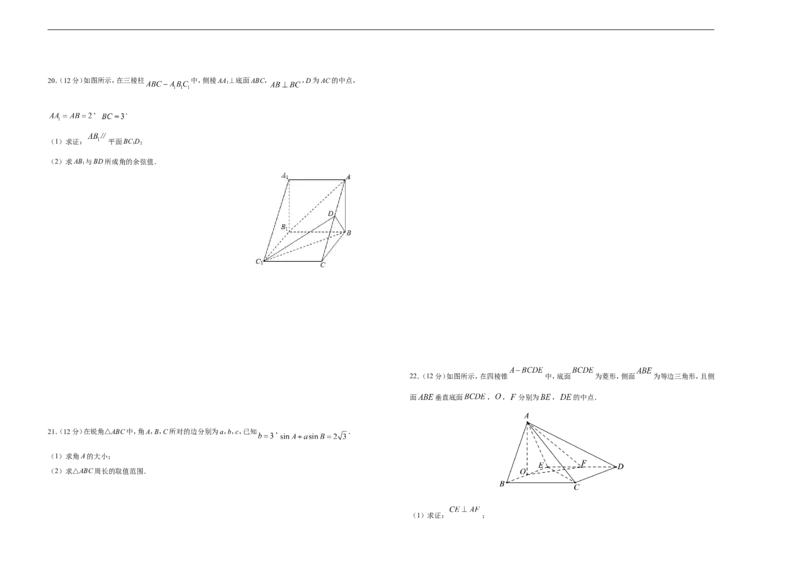
(3)估计居民月均用水量的中位数.20.(12分)如图所示,在三棱柱 中,侧棱AA⊥底面ABC, ,D为AC的中点,
1
, .
(1)求证: 平面BC D;
1
(2)求AB 与BD所成角的余弦值.
1
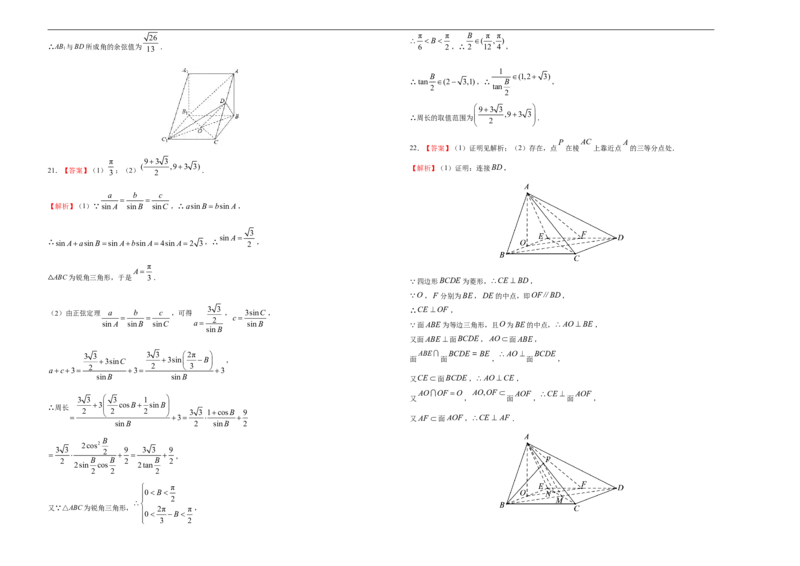
22.(12分)如图所示,在四棱锥 中,底面 为菱形,侧面 为等边三角形,且侧
面 垂直底面 , , 分别为 , 的中点.
21.(12分)在锐角△ABC中,角A,B,C所对的边分别为a,b,c,已知 , .
(1)求角A的大小;
(2)求△ABC周长的取值范围.
(1)求证: ;(2)在棱 上是否存在点 ,使得 平面 ?若存在,请找出点 的位置;若不存在,请说
明理由.(新教材)2020-2021 学年下学期高一期末备考金卷
则 ,
数 学 答 案
,
第Ⅰ卷(选择题)
若比较 与 的大小,只需比较 与 的大小即可,
一、单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是
而 , ,
符合题目要求的.
1.【答案】C
所以 ,
【解析】由已知 ,虚部为 ,
从而 ,故选C.
故选C. 6.【答案】A
2.【答案】A
【解析】由题知, ,根据三角形面积与周长和内心的关系求得,内切圆半径
【解析】由题意得 ,
因为向量 与向量 共线,所以 ,解得 ,
,四边形AEOF为矩形,
故选A.
3.【答案】B
【解析】从随机数表第1行的第9列数字开始由左向右每次连续读取2个数字,删除超出范围及重复
的编号,符合条件的编号有14,05,11,09,
所以选出来的第4个个体的编号为09,故选B.
4.【答案】C
【解析】从1,2,3,4,5这5个数中,选出三个不同的数字组成一个三位数,共有 个三个位数,
则 ,
若这个三位数是3的倍数,则必须是由1,2,3或1,3,5或2,3,4或3,4,5组成的三位数,这一共可
组成 , 又 ,
所以这个三位数是3的倍数的概率为 ,故选C.
则 ,
5.【答案】C
【解析】由已知,两次统计所得的旅游人数总数没有变,
即两次统计的各景点旅游人数的平均数是相同的,设为 ,∴ ,故③正确,
则 ,则 ,
故选B.
故选A.
7.【答案】A
【解析】当开关合上时,电路畅通即表示 至 畅通且 至 畅通,
至 畅通的概率 ,
至 畅通的概率 ,
二、多项选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目
所以电路畅通的概率 ,故选A. 要求.全部选对的得5分,部分选对的得2分,有选错的得0分.
9.【答案】ABD
8.【答案】B
【解析】因为 为整数,
【解析】①∵ ,∴ , ,
所以第75个数据和第76个数据的平均数为第75百分位 ,
又 ,∴ 平面 ,∴ ,故①正确; 所以A、B不正确;C正确;D不正确,
故选ABD.
②假设存在某个位置,使得 ,
10.【答案】BC
连接 ,则 , , 【解析】由复数模的概念可知, 不能得到 ,例如 , ,A错误;
故 平面 ,∴ , 由 可得 ,因为 ,所以 ,即 ,B正确;
又由(1)知 , ,∴ 平面 ,∴ , 因为 , ,而 ,所以 ,所以 ,
C正确;
∴ ,显然这是不可能的,故假设错误,故②错误;
取 , ,显然满足 ,但 ,D错误,
③存在点 ,满足 ,取 的中点 ,连接 ,
故选BC.
易得 , ,
11.【答案】ABD
设底面三角形 的边长为 ,则 , , , 【解析】对于A,由 ,可得 ,利用正弦定理可得 ,正确;
∵ 平面 ,故 平面 ,∴ ,故 是直角三角形, 对于B,在锐角 中, ,不在△OBC内,D错误,
, ,
故选BC.
,因此不等式 恒成立,正确;
第Ⅱ卷(非选择题)
对于C,在 中,由 , 三、填空题:本大题共4小题,每小题5分.
利用正弦定理可得 , ,
13.【答案】
, 或 ,
【解析】由题意,将一枚质地均匀的骰子先后抛掷两次,可得 , ,
或 ,
又由函数 在 上为减函数,则 ,即 ,
是等腰三角形或直角三角形,因此是假命题,C错误;
当 取1时, 可取2,3,4,5,6;
对于D,由于 , ,
当 取2时, 可取4,5,6;
由余弦定理可得 ,可得 ,解得 ,
当 取3时, 可取6,共9种,
可得 ,故正确,
故选ABD.
又因为 的取值共36种情况,
12.【答案】BC
【解析】因为 ,
所以所求概率为 ,故答案为 .
若 且λ>0,则 ,
14.【答案】1
【解析】 复数 满足 为虚数单位),
故 ,即 ,
又λ>0,则点P在线段BC或其反向延长线上,A错误;
设 , ,
若 且λ<0,同上可得 ,而λ<0,则点P在线段BC的延长线上,B正确;
则 ,
若 , ,同上可得 , 当且仅当 时取等号,
故答案为1.
当 时, ,根据向量加法的平行四边形法则可以看出则点P在△OBC外,
15.【答案】
C正确;
【解析】剔除最高分和最低分后的 ,
若 ,不妨令λ=0, ,则 ,很显然此时点P在线段CO的延长线上,,
所以圆锥的内切球半径为 ,
则原始平均分 ,
所以圆锥的内切球的表面积为 ,
原始 ,
故答案为 , .
原始方差 ,
即原始方差为88. 四、解答题:本大题共6个大题,共70分,解答应写出文字说明、证明过程或演算步骤.
16.【答案】 , 17.【答案】(1) ;(2) .
【解析】设圆锥底面圆的半径为 ,母线长为 ,
【解析】(1)由题意,复数 , ,
由题意可得 ,可得 ,
则 ,
由勾股定理可得 ,
因为复数 在复平面上对应的点在第四象限,
所以圆锥的侧面积为 ,
所以 ,解得 ,
即实数 的取值范围 .
(2)由 ,
作圆锥的轴截面如图所示: 、 分别与圆 相切于 两点, 所以 .
设圆 半径为 ,连接 ,则 ,
18.【答案】(1) ;(2) ;(3) .
过点 作 ,则 , ,
【解析】(1)由频率直方图可知,月均用水量在 的频率为 .
所以 ,
0.25
同理,在 , , , , , 的频率分别为 , , ,
所以 ,即 ,解得 ,
0.06,0.04,0.02.
10.040.080.210.250.060.040.020.5a0.5a
a0.30
由 ,解得 .0.060.040.020.12 1 3 3 1 3 3 3 9
(2)由(1)知,100位居民月均用水量不低于3吨的频率为 . PA PA
由题意得, 1 4 4 4 4 8, 2 4 4 16,
由以上样本的频率分布,可以估计30万居民中月均用水量不低于3吨的人数为
2 1 1 2 4 2 2 4
3000000.1236000. PB PB
1 3 3 3 3 9 , 2 3 3 9 .
x
(3)设中位数为 ,
0.040.080.150.210.250.730.5 E AB A B
E
因为前5组的频率之和为 . 设 {甲乙二人共答对3道题},则 1 2 2 1.
0.040.080.150.210.480.5 A B AB A B
而前4组的频率之和为 , 由于 i和 i相互独立, 1 2与 2 1相互互斥,
所以2 x2.5, 3 4 9 4 5
PE PAB PA B PA PB PA PB
所以 1 2 2 1 1 2 2 1 8 9 16 9 12 ,
0.5x20.50.48
x2.04
由 ,解得 ,
5
故可估计居民月均用水量的中位数为2.04.
所以,甲乙二人共答对3道题的概率为12.
3 2 5
p q
19.【答案】(1) 4, 3;(2)12.
26
20.【答案】(1)证明见解析;(2) 13 .
PA p PBq
【解析】(1)设A{甲同学答对第一题},B{乙同学答对第一题},则 , .
【解析】(1)证明:如图,连接BC,设BC与BC 相交于点O,连接OD.
1 1 1
C D=
设 {甲、乙二人均答对第一题}, {甲、乙二人中恰有一人答对第一题}, ∵四边形BCC B 是平行四边形,∴点O为BC的中点.
1 1 1
∵D为AC的中点,∴OD为△ABC的中位线,∴OD∥AB.
C AB D AB AB 1 1
则 , .
∵OD 平面BC D,AB 平面BC D,
1 1 1
由于二人答题互不影响,且每人各题答题结果互不影响, ∴AB 1⊂∥平面BC 1 D. ⊄
A B AB AB (2)解:由(1)可知,∠ODB为AB 与BD所成的角或其补角,
所以 与 相互独立, 与 相互互斥, 1
AB 2 2 OD 2
PC PAB PAPB PD P AB AB ∵AA 1 =AB=2,∴ 1 , ,
所以 ,
AC 13
P AB P AB PAP B P A PB PA 1PB 1PA PB . 在Rt ABC中,D为AC的中点,则 BD 2 2 ,
△
1 1 3 2
pq pq p p 13
OB
2 2 4 3 同理可得 2 ,
由题意可得 5 ,即 17 ,解得 2 或 3 ,
p1qq1 p pq q q
12 12 3 4
在△OBD中,
p
3
q
2
2
13 2 13 2
由于 p q,所以 4, 3.
OD2 BD2 OB2
2
2
2
26 ,
cosODB
2ODBD 13 13
2 2
A i B i i 0 2
(2)设 i {甲同学答对了 道题}, i {乙同学答对了 道题}, ,1,2.π π B π π
26
B ( , )
∴AB 1 与BD所成角的余弦值为 13 . 6 2 ,∴ 2 12 4 ,
1
B (1,2 3)
∴tan (2 3,1),∴ B ,
2 tan
2
93 3
,93 3
∴周长的取值范围为 .
2
P AC A
22.【答案】(1)证明见解析;(2)存在,点 在棱 上靠近点 的三等分点处.
π 93 3
( ,93 3) 【解析】(1)证明:连接BD,
21.【答案】(1)3 ;(2) 2 .
a b c
【解析】(1)∵sin A sinB sinC ,∴asinBbsinA,
3
sin A
∴sin AasinB sin Absin A4sin A2 3,∴ 2 ,
π
A
ABC为锐角三角形,于是 3.
四边形BCDE为菱形,CE BD,
△
O,F 分别为BE,DE的中点,即OF∥BD,
3 3 ∴CE OF ,
(2)由正弦定理 a b c ,可得 , 3sinC ,
c
2
sin A sinB sinC a sinB 面ABE为等边三角形,且O为BE的中点,AO BE ,
sinB
又面ABE 面BCDE,AO面ABE,
3 3 3 3 2π ABE BCDE= BE AO BCDE
3sinC 3sin B , 面 面 , 面 ,
2 2 3
ac3 3 3
sinB sinB 又CE 面BCDE,AOCE ,
AO OF O AO,OF AOF CE AOF
3 3 3 1 又 , 面 , 面 ,
∴周长
3 cosB sinB
2 2 2 3 3 1cosB 9
3 又AF 面AOF ,CE AF .
sinB 2 sinB 2
B
2cos2
3 3 9 3 3 9
2
,
2 B B 2 B 2
2sin cos 2tan
2 2 2
π
0 B
2
又∵△ABC为锐角三角形, 2π π ,
0 B
3 2BD CE M OF CE N
(2)解:设 交 于 , 交 于 ,
则M 为CE的中点,N 为EM 的中点,
在△ACE中,过点M 作MP∥AN 交AC 于点P,则点P即为所求.
理由如下:
O,F 分别为BE,DE的中点,
ON∥BM ,ON 面PBM ,BM 面PBM ,
ON// 面PBM ,同理AN//面PBM ,
ON AN N ON AN AON
, 、 面 ,
面PBM∥面AON ,即面PBM∥面AOF ,
BP面PBM ,BP∥面AOF .
AP NM 1
MP∥AN , AC NC 3,
故点P在棱AC 上靠近点A的三等分点处.