文档内容
高二年级下学期期末仿真卷 01
本试卷共22题。全卷满分150分。考试用时120分钟。
注意事项:
1.答卷前,考生务必将自己的姓名、考生号等填写在答题卡和试卷指定位置上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡对应题目的答案标号涂黑。如需改动,用橡
皮擦干净后,再选涂其他答案标号。回答非选择题时,将答案写在答题卡上。写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
一、选择题:本题共8小题,每小题5分,共40分。在每小题给出的四个选项中,只有一项是符合题目要
求的。
1.等差数列{a}前n项和为S,a+a=5,则S=( )
n n 3 4 6
A.15 B.20 C.25 D.30
【答案】A
【分析】由等差数列的性质易得a+a=a+a=5,而S=3(a+a),代入可得答案.
3 4 1 6 6 1 6
【解答】解:由题意可得a+a=a+a=5,
3 4 1 6
故S=3(a+a)=15
6 1 6
故选:A.
【知识点】等差数列的性质
2.(2x﹣ )5的展开式中x3项的系数为( )
A.80 B.﹣80 C.﹣40 D.48
【答案】B
【分析】利用通项公式即可得出.
【解答】解:通项公式T = =(﹣1)r•25﹣r x5﹣2r,
r+1
令5﹣2r=3,解得r=1.
∴展开式中x3项的系数= =﹣80.
故选:B.
【知识点】二项式定理
3.设f(x)存在导函数且满足 =﹣1,则曲线y=f(x)上的点(1,f(1))处的
切线的斜率为( )
A.﹣1 B.﹣2 C.1 D.2
【答案】A
【分析】根据极限的运算法则的应用,曲线在某处切线斜率的意义即可求出.【解答】解:y=f(x)在点(1,f(1))处的切线的斜率为f′(1)= =﹣1,
故选:A.
【知识点】变化的快慢与变化率、导数及其几何意义
4.《九章算术》是我国古代的数学名著,书中有如下问题:“今有五人分五钱,令上二人所得与下三人等.
问各得几何.”其意思为“已知甲、乙、丙、丁、戊五人分5钱,甲、乙两人所得与丙、丁、戊三人所
得相同,且甲、乙、丙、丁、戊所得依次成等差数列.问五人各得多少钱?”(“钱”是古代的一种重
量单位).这个问题中,甲所得为( )
A. 钱 B. 钱 C. 钱 D. 钱
【答案】B
【分析】依题意设甲、乙、丙、丁、戊所得钱分别为 a﹣2d,a﹣d,a,a+d,a+2d,由题意求得a=﹣
6d,结合a﹣2d+a﹣d+a+a+d+a+2d=5a=5求得a=1,则答案可求.
【解答】解:依题意设甲、乙、丙、丁、戊所得钱分别为a﹣2d,a﹣d,a,a+d,a+2d,
则由题意可知,a﹣2d+a﹣d=a+a+d+a+2d,即a=﹣6d,
又a﹣2d+a﹣d+a+a+d+a+2d=5a=5,∴a=1,
则a﹣2d=a﹣2× = .
故选:B.
【知识点】等差数列的通项公式
5.设x=﹣ 是函数f(x)=ln(x+2)﹣ax2﹣3a2x的极小值点,则f(x)的极大值为( )
A.2 B.1 C. D.
【答案】D
【分析】求函数的导函数,利用极小值点求出a的值,再确定出函数的解析式,从而确定函数的极大值.
【解答】解:函数f(x)=ln(x+2)﹣ax2﹣3a2x,定义域是:{x|x>﹣2}
f′(x)= ﹣2ax﹣3a2
因为x=﹣ 是函数f(x)=ln(x+2)﹣ax2﹣3a2x的极小值点,
则:f′(﹣ )=0,解得:9a2﹣3a﹣2=0,即:a=﹣ ,或 a= ,
讨论a;
①当a=﹣ 时,函数f′(x)= + x﹣ = ,
在(﹣2,﹣1),f′(x)>0
在(﹣1,﹣ )f′(x)<0
在(﹣ ,+∞)f′(x)>0∴函数f(x)在x=﹣ 取得极小值点,在x=﹣1取得极大值点,
∵函数定义域是:{x|x>﹣2}
∴f(x)的极大值为f(﹣1)=
②当 a= 时,函数f′(x)= ﹣ x﹣ =﹣ ,
在(﹣2,﹣ ),f′(x)>0
在(﹣ ,+∞),f′(x)<0
∴x=﹣ 不是函数f(x)=ln(x+2)﹣ax2﹣3a2x的极小值点,与题设矛盾,a= 舍去.
综合可得:x=﹣ 是函数f(x)=ln(x+2)﹣ax2﹣3a2x的极小值点时,f(x)的极大值为:
.
故选:D.
【知识点】利用导数研究函数的极值
6.2019年10月17日是我国第6个“扶贫日”,某医院开展扶贫日“送医下乡”医疗义诊活动,现有五名
医生被分配到四所不同的乡镇医院中,医生甲被指定分配到医院 A,医生乙只能分配到医院A或医院
B,医生丙不能分配到医生甲、乙所在的医院,其他两名医生分配到哪所医院都可以,若每所医院至少
分配一名医生,则不同的分配方案共有( )
A.18种 B.20种 C.22种 D.24种
【答案】B
【分析】根据题意,分4种情况讨论:①甲乙都分到A医院,②甲分配到医院A,乙分配到医院B,③甲
和一名医生一起分到A医院,乙在B医院,④甲单独分到A医院,乙和一名医生一起分到B医院,
由加法原理计算可得答案.
【解答】解:根据题意,分4种情况讨论:
①甲乙都分到A医院,剩下3人全排列,分配到其三个医院,有A3=6种分派方案;
3
②甲分配到医院A,乙分配到医院B,剩下3人分成2组,安排到C、D医院,有C 2A2=6种
3 2
分派方案;
③甲和一名医生一起分到A医院,乙在B医院,剩下2人全排列,安排到C、D医院,有
C 1A2=4种分派方案;
2 2
④甲单独分到A医院,乙和一名医生一起分到B医院,剩下2人全排列,安排到C、D医院,
有C 1A2=4种分派方案;
2 2
则一共有6+6+4+4=20种分配方案;
故选:B.
【知识点】排列、组合及简单计数问题
7.2019年10月1日在庆祝中华人民共和国成立70周年大阅兵的徒步方队中,被誉为“最强大脑”的院校
科研方队队员分别由军事科学院、国防大学、国防科技大学三所院校联合抽组,已知军事科学学院的甲、乙、丙三名同学被选上的概率分别为 , , ,这三名同学中至少有一名同学被选上的概率为
( )
A. B. C. D.
【答案】C
【分析】利用对立事件概率计算公式直接求解.
【解答】解:军事科学学院的甲、乙、丙三名同学被选上的概率分别为 , , ,
∴这三名同学中至少有一名同学被选上的概率为:
P=1﹣(1﹣ )(1﹣ )(1﹣ )= .
故选:C.
【知识点】相互独立事件和相互独立事件的概率乘法公式
8.某种商品的广告费支出x与销售额y(单位:万元)之间有如下对应数据,根据表中提供的数据,得出 y
与x的线性回归方程为 ,则表中的m的值为( )
x 2 4 5 6 8
y 30 40 m 50 70
A.45 B.50 C.55 D.60
【答案】D
【分析】计算样本中心点,根据线性回归方程恒过样本中心点,即可得到结论.
【解答】解:由题意, = =5,
= =38+ ,
∵y关于x的线性回归方程为 ,
∴38+ =6.5×5+17.5
∴38+ =50
∴ =12,
∴m=60
故选:D.
【知识点】线性回归方程二、多选题:本题共4小题,每小题5分,共20分。在每小题给出的四个选项中,有多项是符合题目要求
的,选对得分,错选或漏选不得分。
9.对于二项式 ,以下判断正确的有( )
A.存在n N*,展开式中有常数项
B.对任意∈n N*,展开式中没有常数项
C.对任意n∈N*,展开式中没有x的一次项
D.存在n N∈*,展开式中有x的一次项
【答案】AD∈
【分析】本题考查二项式定理,只要能写出二项展开式的通项,就可选出答案,属于简单题.
【解答】解:该二项展开式的通项为 ,
∴当n=4k时,展开式中存在常数项,A选项正确,B选项错误;
当n=4k﹣1时,展开式中存在x的一次项,D选项正确,C选项错误.
故选:AD.
【知识点】二项式定理
10.甲罐中有5个红球,2个白球和3个黑球,乙罐中有4个红球,3个白球和3个黑球.先从甲罐中随机取
出一球放入乙罐,分别以A ,A 和A 表示由甲罐取出的球是红球,白球和黑球的事件;再从乙罐中随
1 2 3
机取出一球,以B表示由乙罐取出的球是红球的事件,则下列结论中正确的是( )
A.
B.
C.事件B与事件A 相互独立
1
D.A,A,A 是两两互斥的事件
1 2 3
【答案】BD
【分析】本题是概率的综合问题,掌握条件概率的基本运算是解决问题的关键.本题在A ,A ,A 是两两
1 2 3
互斥的事件,把事件B的概率进行转化P(B)=P(B|•A)+P(B•A)+P(B•A),可知事件B
1 2 3
的概率是确定的.
【 解 答 】 解 : 易 见 A , A , A 是 两 两 互 斥 的 事 件 ,
1 2 3
.
故选:BD.
【知识点】相互独立事件和相互独立事件的概率乘法公式
11.设等比数列{a}的公比为q,其前n项和为S ,前n项积为T ,并满足条件a >1,且a a >1,
n n n 1 2020 2021
(a ﹣1)(a ﹣1)<0,下列结论正确的是( )
2020 2021
A.S <S
2020 2021B.a a ﹣1<0
2020 2022
C.数列{T}无最大值
n
D.T 是数列{T}中的最大值
2020 n
【答案】ABD
【分析】根据题意,分析可得a >1,a <1,从而有a>1,0<q<1,则等比数列{a}为正项的递减数
2020 2021 1 n
列.再结合等比数列的性质逐一核对四个命题得答案即可得到正确选项.
【解答】解:根据题意,根据题意,等比数列{a}的公比为q,若a a >1,则(aq2019)(aq2020)=
n 2020 2021 1 1
(a)2(q4039)>1,
1
又由a>1,必有q>0,则数列{a}各项均为正值,
1 n
若(a ﹣1)(a ﹣1)<0,必有a >1,0<a <1,则必有0<q<1,
2020 2021 2020 2021
依次分析选项:
对于A,数列{a}各项均为正值,则S ﹣S =a >0,必有S <S ,A正确;
n 2021 2020 2021 2020 2021
对于B,若0<a <1,则a a ﹣1=(a )2﹣1<0,B正确,
2021 2020 2022 2021
对于C,根据a>a>…>a >1>a >…>0,可知T 是数列{T}中的最大项,C错误;
1 2 2020 2021 2020 n
对于D,易得D正确,
故选:ABD.
【知识点】等比数列的前n项和
12.如果函数y=f(x)的导函数y=f'(x)的图象如图所示,则以下关于函数y=f(x)的判断正确的是(
)
A.在区间(2,4)内单调递减
B.在区间(2,3)内单调递增
C.x=﹣3是极小值点
D.x=4是极大值点
【答案】BD
【分析】利用导函数的图象,判断导函数的符号,判断函数的单调区间以及函数的极值即可.
【解答】解:A.函数y=f(x)在区间(2,4)内f′(x)>0,则函数单调递增;故A不正确,
B.函数y=xf′(x)在区间(2,3)的导数为f′(x)>0,
∴y=f(x)在区间(2,3)上单调递增,∴B正确;
C.由图象知当x=﹣3时,函数f′(x)取得极小值,但是函数y=f(x)没有取得极小值,
故C错误,
D.x=4时,f'(x)=0,
当2<x<4时,f′(x)>0,f′(x)为增函数,4<x,此时f′(x)<0此时函数y=f(x)为减函数,
则函数y=f(x)内有极大值,x=4是极大值点;故D正确,
故选:BD.
【知识点】利用导数研究函数的极值
三、填空题:本题共4小题,每小题5分,共20分。
13.某幼儿园的2名老师带着5名学生排队过马路,要求前后必须各有一名老师监护,则不同的排法共
种.
【答案】240
【分析】根据题意,分2步进行分析:①将2名老师安排在两端,②将5名学生全排列,安排在2名老师
中间,由分步计数原理计算可得答案.
【解答】解:根据题意,分2步进行分析:
①要求前后必须各有一名老师监护,需要将2名老师安排在两端,则2名老师的排法有2种,
②将5名学生全排列,安排在2名老师中间,有A5=120种排法,
5
则有2×120=240种排法,
故答案为:240.
【知识点】排列、组合及简单计数问题
14.2019年10月22日,联合国教科文组织公布2019年度联合国教科文组织﹣赤道几内亚国际生命科学研
究奖获奖名单,共3人获奖,其中包括来自中国的屠呦呦.中国中医科学院教授、2015年诺贝尔生理学
或医学奖获得者屠呦呦发现的全新抗疟疾药物青蒿素在20世纪80年代治愈了许多中国病人.某科研机
构为了了解某种在研制的药品的指标数据y与百分比浓度p之间的关系,随机统计了某5次实验的相关
数据,并制作了对照表如表:
百分比浓度 6 10 14 18 22
p
指标数据y 62 m 44 28 14
由表中数据求得回归直线方程为 =﹣3p+82.2,则m= .
【答案】53
【分析】求出样本中心坐标,代入回归直线方程,求解即可.
【解答】解:由题意 = =14,
= = ,所以样本中心为(14, ),
因为回归直线经过样本中心,所以 =﹣3×14+82.2,解得m=53.
故答案为:53.
【知识点】线性回归方程
15.对一个物理量做n次测量,并以测量结果的平均值作为该物理量的最后结果.已知最后结果的误差 ε ~
nN(0, ),为使误差ε 在(﹣0.5,0.5)的概率不小于0.9545,至少要测量 次.(若X~N( ,
n
μ
σ2),则P(|X﹣ |<2σ)=0.9545).
【答案】32 μ
【分析】根据正态曲线的对称性知,要使得误差ε 在(﹣0.5,0.5)的概率不小于0.9545,问题转化为(
n
﹣2σ, +2σ)⊂(﹣0.5,0.5)且 =σ,σ= ,可求. μ
【解答】解:根据μ 正态曲线的对称性知,要μ使得误差ε 在(﹣0.5,0.5)的概率不小于0.9545,
n
则( ﹣2σ, +2σ)⊂(﹣0.5,0.5)且 =σ,σ= ,
μ μ μ
所以0.5 ,
解得,n≥32,即n的最小值32.
故答案为:32.
【知识点】正态分布曲线的特点及曲线所表示的意义
16.定义max{a,b}= 且f(x)= ﹣2e,g(x)= ,令h(x)=max{f(x),g(x)},
则h(x)的极大值为 ,单调递增区间为 .
【分析】对g(x)求导,分析g′(x)的正负,g(x)的单调性,作出h(x)=max{f(x),g(x)}的
大致图象如下:
h(x)的单调递增区间为[ ,e].
【解答】解:因为g(x)= (x>0),
所以g′(x)= ,
令g′(x)=0,则x=e,
当0<x<e时,g′(x)>0,g(x)单调递增,
当x>e时,g′(x)<0,g(x)单调递减,
所以g(x) =g(e)= ,
极大值
由f(x)=g(x),即x﹣2e= ,得x= ,
作出h(x)=max{f(x),g(x)}的大致图象如下:则h(x) =g(e)= ,且在(0, ),(e,+∞)上单调递减,
极大值
在[ ,e]上单调递增,
则h(x)的单调递增区间为[ ,e].
故答案为: ,[ ,e].
【知识点】利用导数研究函数的极值
四、解答题:共70分。解答应写出文字说明、证明过程或演算步骤。考生根据要求作答。
17.S 为等比数列{a}的前n项和,已知a=9a,S=13,且公比q>0.
n n 4 2 3
(1)求a 及S;
n n
(2)是否存在常数 ,使得数列{S+ }是等比数列?若存在,求 的值;若不存在,请说明理由.
n
λ λ λ
【分析】(1)由题意可得 ,解得a=1,q=3,根据通项公式和求和公式即可求出,
1
(2)假设存在常数 ,使得数列{S+ }是等比数列,分别令n=1,2,3,根据等比数列的性
n
质求出 的值,再根据定义证明即可.
λ λ
λ
【解答】解:(1)由题意可得 ,解得a=1,q=3,
1
∴a=3n﹣1,S= = ,
n n
(2)假设存在常数 ,使得数列{S+ }是等比数列,
n
λ λ∵S+ = +1,S+ = +4,S+ = +13,
1 2 3
∴( +4)2=( +1)( +13),
λ λ λ λ λ λ
解得λ= , λ λ
λ
此时S+ = ×3n,
n
λ
则 =3,
故存在常数 ,使得数列{S+ }是等比数列.
n
【知识点】等比数列的前n项和
18.已知数列{a}的前n项和为 ,数列{b}满足b=log a.
n n n 2 n
(1)求数列{a}、{b}的通项公式;
n n
(2)求T=b2﹣b2+b2﹣b2+…+(﹣1)n+1b2.
n 1 2 3 4 n
【分析】本题第(1)题先根据组合的知识可知S=2n﹣1,然后根据公式a= 可计算出
n n
数列{a}的通项公式,最后将数列{a}的通项公式代入b =log a 进行计算可得数列{b}的通项公
n n n 2 n n
式;
第(2)题先根据第(1)题的结果可判断出数列{b}是以0为首项,1为公差的等差数列,然
n
后对n分奇数和偶数两种情况分别进行计算,利用平方差公式及等差数列的求和公式可计算出
T 的表达式.
n
【解答】解:(1)由题意, =2n﹣1,
当n=1时,a=S=21﹣1=1,
1 1
当n≥2时,a=S﹣S =2n﹣1﹣2n﹣1+1=2n﹣1,
n n n﹣1
∵当n=1时,a=1也满足a=2n﹣1,
1 n
∴a=2n﹣1,n N*,
n
∴b=log a=log 2n﹣1=n﹣1,n N*.
n 2 n 2
∈
(2)由(1)知,b=n﹣1=0+1•(n﹣1),
n
∈
故数列{b}是以0为首项,1为公差的等差数列,
n
①当n为奇数时,n﹣1为偶数,
T=b2﹣b2+b2﹣b2+…+(﹣1)n+1b2
n 1 2 3 4 n
=b2﹣b2+b2﹣b2+…+b 2﹣b 2+b2
1 2 3 4 n﹣2 n﹣1 n
=(b+b)(b﹣b)+(b+b)(b﹣b)+…+(b +b )(b ﹣b )+b2
1 2 1 2 3 4 3 4 n﹣2 n﹣1 n﹣2 n﹣1 n
=﹣(b+b+b+b+…+b +b )+b2
1 2 3 4 n﹣2 n﹣1 n
=﹣ +(n﹣1)2
= ;②当n为偶数时,n﹣1,n+1均为奇数,
T=b2﹣b2+b2﹣b2+…+(﹣1)n+1b2
n 1 2 3 4 n
=b2﹣b2+b2﹣b2+…+b 2﹣b2
1 2 3 4 n﹣1 n
=(b+b)(b﹣b)+(b+b)(b﹣b)+…+(b +b)(b ﹣b)
1 2 1 2 3 4 3 4 n﹣1 n n﹣1 n
=﹣(b+b+b+b+…+b +b)
1 2 3 4 n﹣1 n
=﹣
= ;
综上所述,可知:
T= .
n
【知识点】数列的求和、组合及组合数公式
19.为了贯彻落实党中央对新冠肺炎疫情防控工作的部署和要求,坚决防范疫情向校园蔓延,切实保障广大
师生身体健康和生命的安全,教育主管部门决定通过电视频道、网络平台等多种方式实施线上教育教学
工作.某教育机构为了了解人们对其数学网课授课方式的满意度,从经济不发达的 A城市和经济发达的
B城市分别随机调查了20个用户,得到了一个用户满意度评分的样本,并绘制出茎叶图如图:
若评分不低于80分,则认为该用户对此教育机构授课方式“认可”,否则认为该用户对此教育机构授课方
式“不认可”.
(Ⅰ)请根据此样本完成下列2×2列联表,并据此列联表分析,能否有95%的把握认为城市经济状况与该
市的用户认可该教育机构授课方式有关?
认可 不认可 合计
A城市
B城市
合计
(Ⅱ)以该样本中A,B城市的用户对此教育机构授课方式“认可”的频率分别作为 A,B城市用户对此教育机构授课方式“认可”的概率.现从A城市和B城市的所有用户中分别随机抽取2个用户,用X表示这
4个用户中对此教育机构授课方式“认可”的用户个数,求x的分布列.
参考公式: ,其中n=a+b+c+d.
参考数据:
P(K2≥K) 0.10 0.05 0.025
k 2.706 3.841 5.024
【答案】【第1空】5
【第2空】15
【第3空】20
【第4空】10
【第5空】10
【第6空】20
【第7空】15
【第8空】25
【第9空】40
【分析】(Ⅰ)根据茎叶图可完成列联表,再根据公式求出K2,再与3.841比较大小即可求出结论;
(Ⅱ)由题意可得,X的取值可能为0,1,2,3,4,再根据相互独立事件与互斥事件的概率
公式即可求出分布列.
【解答】解:(Ⅰ)有茎叶图可得列联表如下:
认可 不认可 合计
A城市 5 15 20
B城市 10 10 20
合计 15 25 40
∴ ,
∴没有95%的把握认为城市经济状况与该市的用户认可该教育机构授课方式有关;
(Ⅱ)由题意知,A城市用户对此教育机构授课方式“认可”的概率为 ,
B城市用户对此教育机构授课方式“认可”的概率为 ,
X的可能结果为0,1,2,3,4,
P(X=0)= ,
P(X=1)= + = ,
P ( X = 2 ) = =,
P(X=3)= = ,
P(X=4)= ,
∴X的分布列为
X 0 1 2 3 4
P
【知识点】独立性检验、离散型随机变量及其分布列
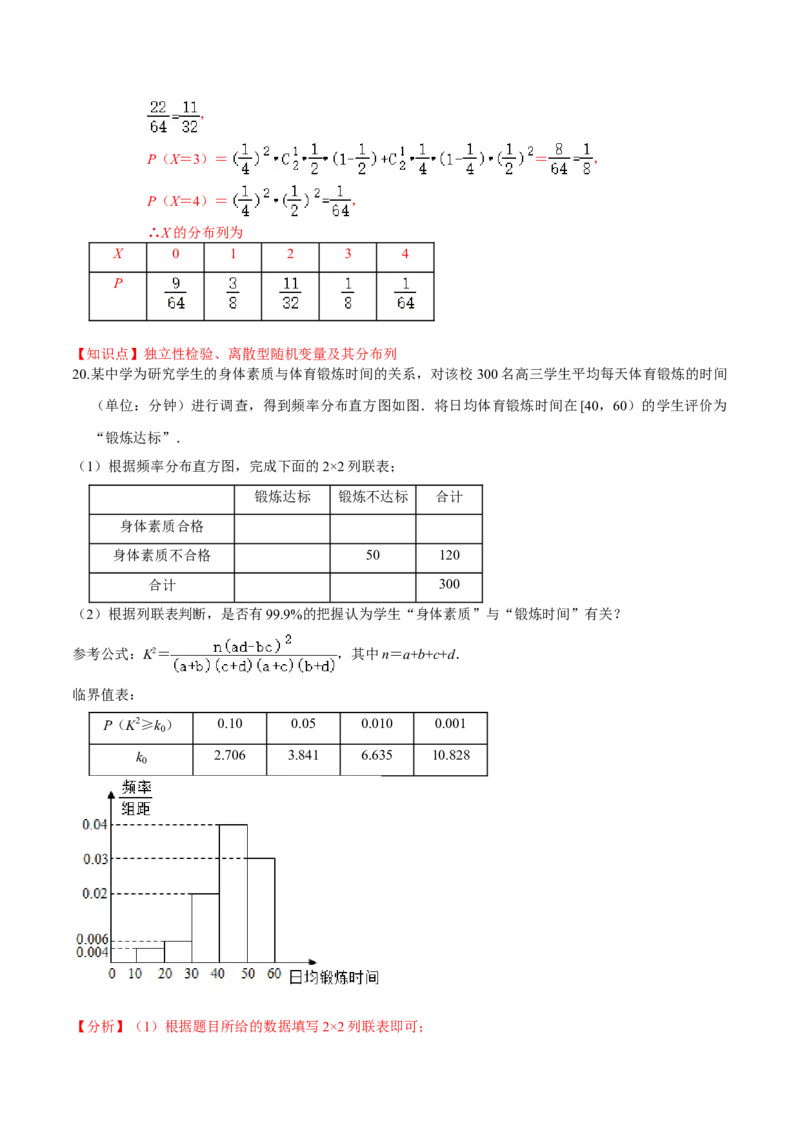
20.某中学为研究学生的身体素质与体育锻炼时间的关系,对该校300名高三学生平均每天体育锻炼的时间
(单位:分钟)进行调查,得到频率分布直方图如图.将日均体育锻炼时间在[40,60)的学生评价为
“锻炼达标”.
(1)根据频率分布直方图,完成下面的2×2列联表;
锻炼达标 锻炼不达标 合计
身体素质合格
身体素质不合格 50 120
合计 300
(2)根据列联表判断,是否有99.9%的把握认为学生“身体素质”与“锻炼时间”有关?
参考公式:K2= ,其中n=a+b+c+d.
临界值表:
P(K2≥k ) 0.10 0.05 0.010 0.001
0
k 2.706 3.841 6.635 10.828
0
【分析】(1)根据题目所给的数据填写2×2列联表即可;(2)计算K的观测值K2,并与附录中的数据进行对比即可作出判断.
【解答】解:(1)由频率分布直方图可知,“锻炼达标”的人数为300×(0.03+0.04)×10=210.
补充完整的2×2列联表如下:
锻炼达标 锻炼不达标 合计
身体素质合格 140 40 180
身体素质不合格 70 50 120
合计 210 90 300
(2)K2= = ≈12.963>10.828,
故有99.9%的把握认为学生“身体素质”与“锻炼时间”有关.
【知识点】独立性检验
21.在集合A={1,2,3,4,…,2n}中,任取m(m≤n,m,n N*)元素构成集合A .若A 的所有元素
m m
之和为偶数,则称A 为A的偶子集,其个数记为f(m);若∈ A 的所有元素之和为奇数,则称A 为A
m m m
的奇子集,其个数记为g(m).令F(m)=f(m)﹣g(m).
(1)当n=2时,求F(1),F(2)的值;
(2)求F(m).
【分析】(1)当n=2时,根据定义即可求F(1),F(2)
(2)分别讨论当m是奇数和偶数时,f(m)和g(m)的值,利用二项式定理进行求解即可.
【解答】解:(1)当n=2时,集合为{1,2,3,4}.
当m=1时,偶子集有{2},{4},奇子集有{1},{3},f(1)=2,g(1)=2,F(1)=0;
当m=2时,偶子集有{2,4},{1,3},奇子集有{1,2},{1,4},{2,3},{3,4},
f(2)=2,g(2)=4,F(2)=﹣2;
(2)当m为奇数时,偶子集的个数f(m)=
∁n
0
n
m+
n
2
n
m﹣2+
n
4
n
m﹣4+…+
n
m﹣1
n
1,
奇子集的个数g(m)=
∁n
1
n
m﹣1+
n
3
n
m﹣3+…+
n
m
n
0,
∁ ∁ ∁ ∁ ∁ ∁ ∁
所以f(m)=g(m),F(m)=f(m)﹣g(m)=0.
∁ ∁ ∁ ∁ ∁
当m为偶数时,偶子集的个数
∁n
0
n
m+
n
2
n
m﹣2+
n
4
n
m﹣4+…+
n
m
n
0,
奇子集的个数g(m)=
∁n
1
n
m﹣1+
n
3
n
m﹣3+…+
n
m﹣1
n
1,
∁ ∁ ∁ ∁ ∁ ∁ ∁
所以F(m)=f(m)﹣g(m)=
∁n
0
n
m﹣
∁n
1
n
m﹣1+
n
2
n
m﹣2﹣
∁n
3
n
m﹣3+…﹣
∁n
m﹣1
n
1+
n
m
n
0,
∁ ∁ ∁ ∁ ∁
一方面,
∁ ∁ ∁ ∁ ∁ ∁ ∁ ∁
(1+x)m(1﹣x)m=(
∁m
0+
m
1x+
m
2x2+…+
m
mxm)((
∁m
0﹣
∁m
1x+
m
2x2+…+(﹣1)m
m
mxm),
所以(1+x)m(1﹣x)m中xm的系数为
∁ ∁ ∁ ∁ ∁
m
0
m
m﹣
∁m
1
m
m﹣1+
m
2
m
m﹣2﹣
∁m
3
m
m﹣3+…﹣
∁m
m﹣1
m
1+
m
m
m
0,
另一方面,
∁ ∁ ∁ ∁ ∁ ∁ ∁ ∁ ∁
(1+x)m(1﹣x)m=(1+x)m(1﹣x2)m中,(1﹣x2)m中xm的系数为(﹣1) ,
故F(m)=(﹣1) ,综上,F(m)= .
【知识点】二项式定理
22.已知函数f(x)=(x﹣1)lnx+ax2+(1﹣a)x﹣1.
(1)当a=﹣1时,判断函数的单调性;
(2)讨论f(x)零点的个数.
【分析】(1)把a=﹣1代入后对函数求导,然后结合导数与单调性的关系即可求解函数的单调性;
(2)先对函数求导,然后结合导可判断函数的单调性,然后结合函数的性质及零点判定定理
即可求解.
【解答】解:(1)a=﹣1时,f(x)=(x﹣1)lnx﹣x2+2x﹣1, ,
令h(x)= ,则 = ,
易得函数h(x)在(0,1)上单调递增,在(1,+∞)上单调递减,
故h(x)≤h(1)=0即f′(x)≤0,
所以f(x)在(0,+∞)上单调递减;
(2)由f(x)=(x﹣1)lnx+ax2+(1﹣a)x﹣1可得f(1)=0,即x=1为函数f(x)的一个
零点,
设g(x)=lnx+ax+1,则f(x)的零点个数即为g(x)的不为1的零点个数加上1,
(i)当a=﹣1时,由(1)知f(x)单调递减,且x=1是f(x)的零点,故f(x)有且只有1
个零点1;
(ii)当a≥0时,g(x)单调递增且g(1)>0,
g(x)=lnx+ax+1< = ,0<x<1,
因为ax2+(a+3)x﹣1<(a+4)x2+(a+3)x﹣1=[(a+4)x﹣1](x+1),
所以g( )<0,
综上可知,g(x)在(0,+∞)上有1个零点且g(1)=9,
所以f(x)有2个零点
(iii)又 ,所以当﹣1<a<0时,g(x)在(0,﹣ )上单调递增,在(﹣
)上单调递减,
故g(x)的最大值g(﹣ )=ln(﹣ )>0,
又g(x)< =0,且g( )<0,g( )= <0,
所以g(x)在(0,﹣ )上有1个零点,在(﹣ )上有1个零点且x=0也是零点,
此时f(x)共有3个零点,(iv)又 ,所以当 a<﹣1时,g(x)在(0,﹣ )上单调递增,在(﹣
)上单调递减,
故g(x)的最大值g(﹣ )=ln(﹣ )<0,
故g(x)没有零点,此时f(x)只有1个零点,
综上可得,当a≤﹣1时,f(x)有1个零点;当﹣1<a<0时,f(x)有3个零点,当a≥0时,
f(x)有2个零点.
【知识点】利用导数研究函数的单调性