文档内容
期中检测卷 02
姓名:__________________ 班级:______________ 得分:_________________
注意事项:
本试卷满分150分,考试时间120分钟,试题共22题.答卷前,考生务必用0.5毫米黑色签字笔将自
己的姓名、班级等信息填写在试卷规定的位置.
一、选择题(本大题共8小题,每小题5分,共40分)在每小题所给出的四个选项中,只有一项是符合题
目要求的.
1.点C是线段AB靠近点B的三等分点,下列正确的是( )
A. B. C. D.
2.已知复数z满足z(3+i)=3+i2020,其中i为虚数单位,则z的共轭复数 的虚部为( )
A. B. C. D.
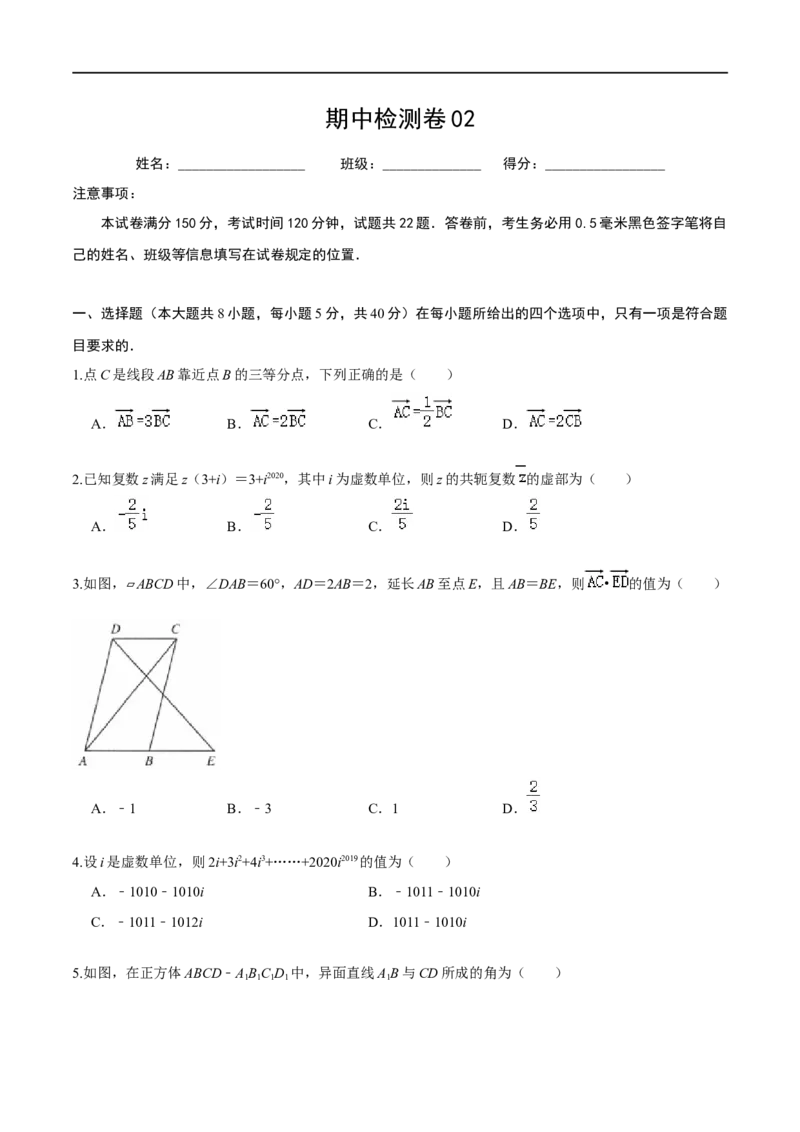
3.如图, ▱ABCD中,∠DAB=60°,AD=2AB=2,延长AB至点E,且AB=BE,则 • 的值为( )
A.﹣1 B.﹣3 C.1 D.
4.设i是虚数单位,则2i+3i2+4i3+……+2020i2019的值为( )
A.﹣1010﹣1010i B.﹣1011﹣1010i
C.﹣1011﹣1012i D.1011﹣1010i
5.如图,在正方体ABCD﹣ABC D 中,异面直线AB与CD所成的角为( )
1 1 1 1 1A.30° B.45° C.60° D.135°
6.在△ABC中,角A,B,C所对的边分别为a,b,c,若(a﹣2b)cosC=c(2cosB﹣cosA),△ABC的面
积为a2sin ,则C=( )
A. B. C. D.
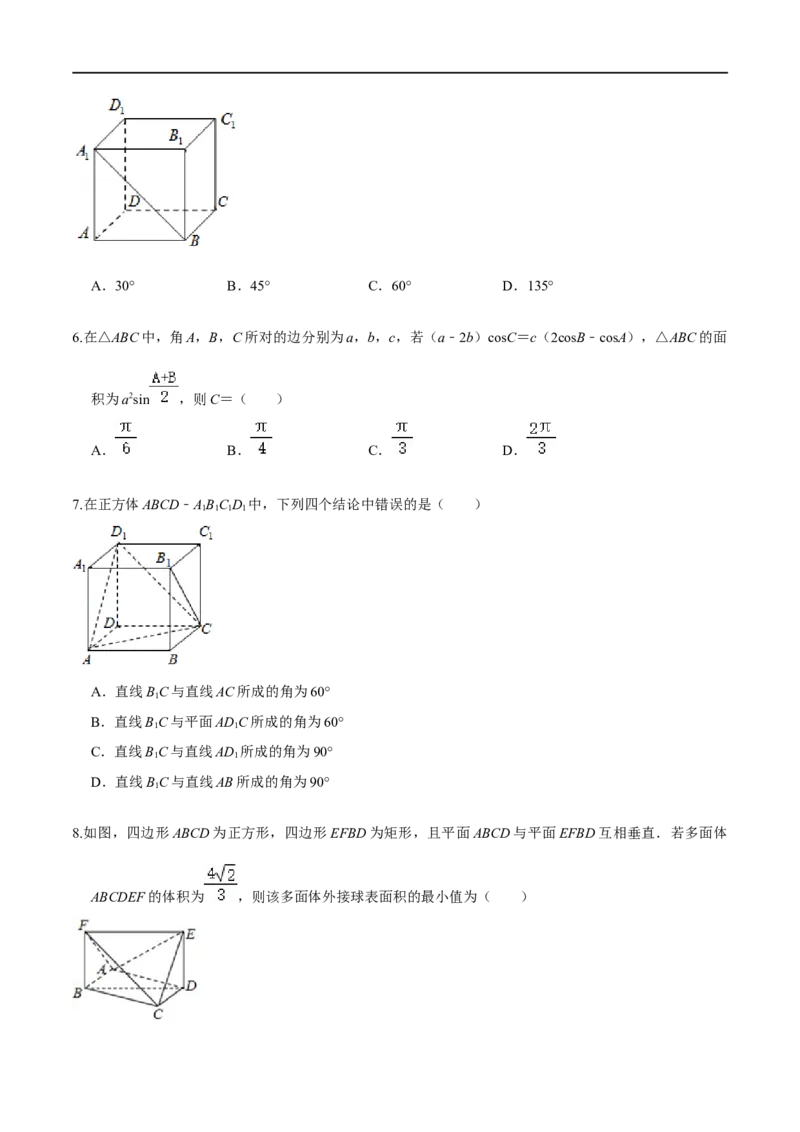
7.在正方体ABCD﹣ABC D 中,下列四个结论中错误的是( )
1 1 1 1
A.直线BC与直线AC所成的角为60°
1
B.直线BC与平面ADC所成的角为60°
1 1
C.直线BC与直线AD 所成的角为90°
1 1
D.直线BC与直线AB所成的角为90°
1
8.如图,四边形ABCD为正方形,四边形EFBD为矩形,且平面ABCD与平面EFBD互相垂直.若多面体
ABCDEF的体积为 ,则该多面体外接球表面积的最小值为( )A.6 B.8 C.12 D.16
二、多选π题(本大题共4小题,π每小题5分,选对得分π,选错、少选不得分)π
9.在△ABC中,角A,B,C的对边分别为a,b,c,若a2=b2+bc,则角A可为( )
A. B. C. D.
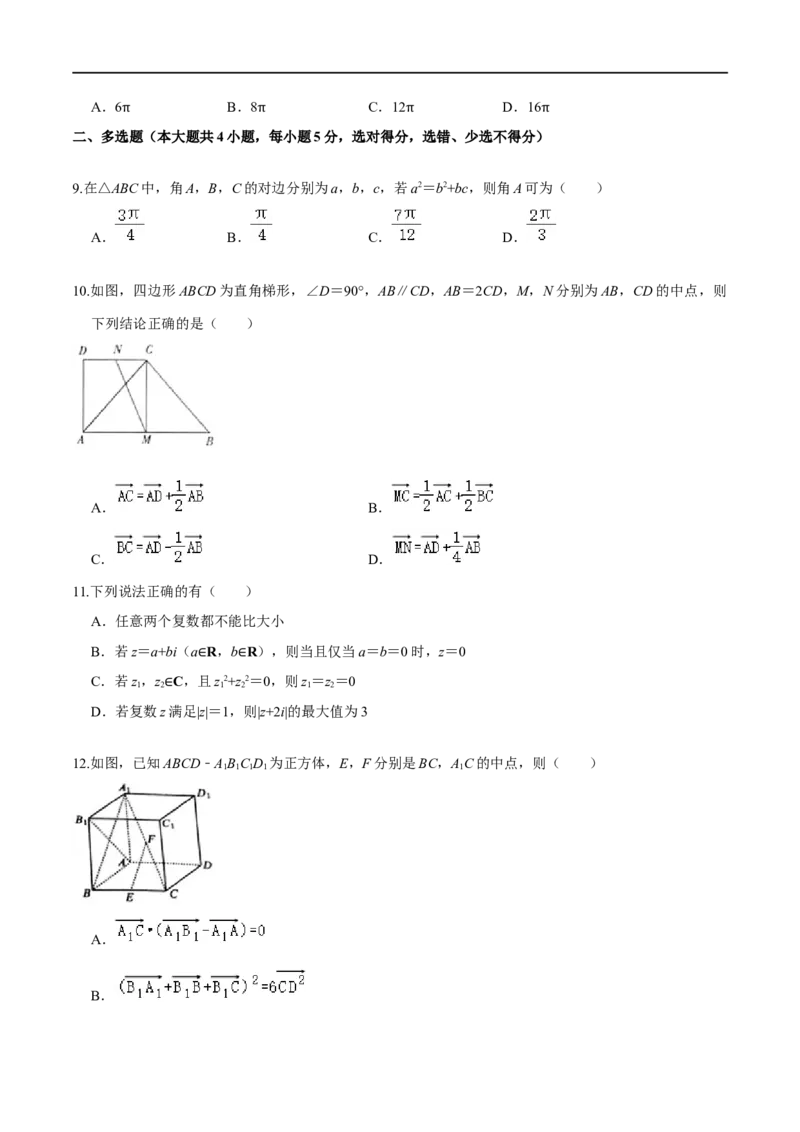
10.如图,四边形ABCD为直角梯形,∠D=90°,AB∥CD,AB=2CD,M,N分别为AB,CD的中点,则
下列结论正确的是( )
A. B.
C. D.
11.下列说法正确的有( )
A.任意两个复数都不能比大小
B.若z=a+bi(a R,b R),则当且仅当a=b=0时,z=0
C.若z,z C,且∈ z2+z∈2=0,则z=z=0
1 2 1 2 1 2
D.若复数z∈满足|z|=1,则|z+2i|的最大值为3
12.如图,已知ABCD﹣ABC D 为正方体,E,F分别是BC,AC的中点,则( )
1 1 1 1 1
A.
B.C.向量 与向量 的夹角是60°
D.异面直线EF与DD 所成的角为45°
1
三、填空题(本大题共4小题,每小题5分,共20分.不需写出解答过程,请把答案直接填写在横线上)
13.已知正方形ABCD的边长为2,点P满足 = ( + ),则| |= ; • = .
14.若虛数z、z 是实系数一元二次方程x2+px+q=0的两个根,且 ,则pq= .
1 2
15.已知平面四边形ABCD中,AB=AD=2,BC=CD=BD=2 ,将△ABD沿对角线BD折起,使点A到
达点A'的位置,当A'C= 时,三棱锥A﹣BCD的外接球的体积为 .
16.已知一圆锥底面圆的直径为3,圆锥的高为 ,在该圆锥内放置一个棱长为a的正四面体,并且正四
面体在该几何体内可以任意转动,则a的最大值为 .
四、解答题(本大题共6小题,共70分.请在答题卡指定区域内作答,解答时应写出文字说明、证明过程
或演算步骤)
17.在四边形ABCD中,AB∥CD,AD=BD=CD=1.
(1)若AB= ,求BC;
(2)若AB=2BC,求cos∠BDC.
18.(1)已知z=1﹣2i,z=3+4i,求满足 = + 的复数z.
1 2(2)已知z,ω为复数,(1+3i)﹣z为纯虚数,ω= ,且|ω|=5 .求复数ω.
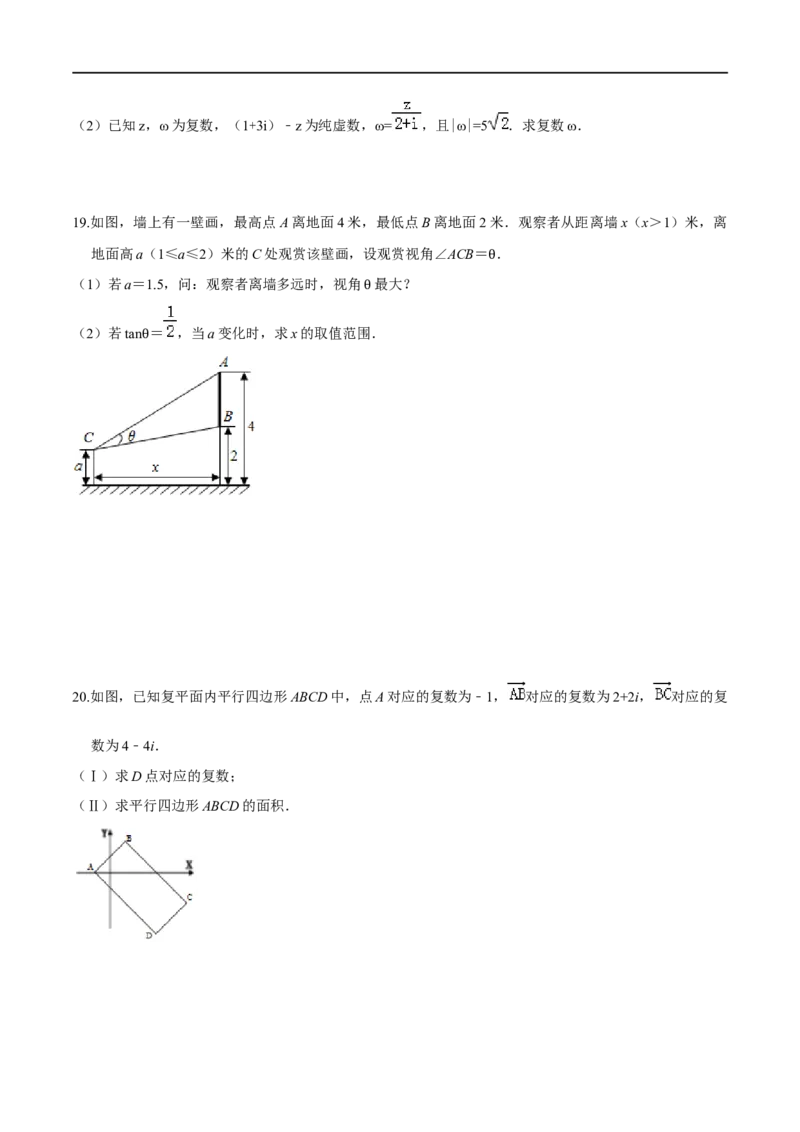
19.如图,墙上有一壁画,最高点A离地面4米,最低点B离地面2米.观察者从距离墙x(x>1)米,离
地面高a(1≤a≤2)米的C处观赏该壁画,设观赏视角∠ACB= .
(1)若a=1.5,问:观察者离墙多远时,视角 最大? θ
θ
(2)若tan = ,当a变化时,求x的取值范围.
θ
20.如图,已知复平面内平行四边形ABCD中,点A对应的复数为﹣1, 对应的复数为2+2i, 对应的复
数为4﹣4i.
(Ⅰ)求D点对应的复数;
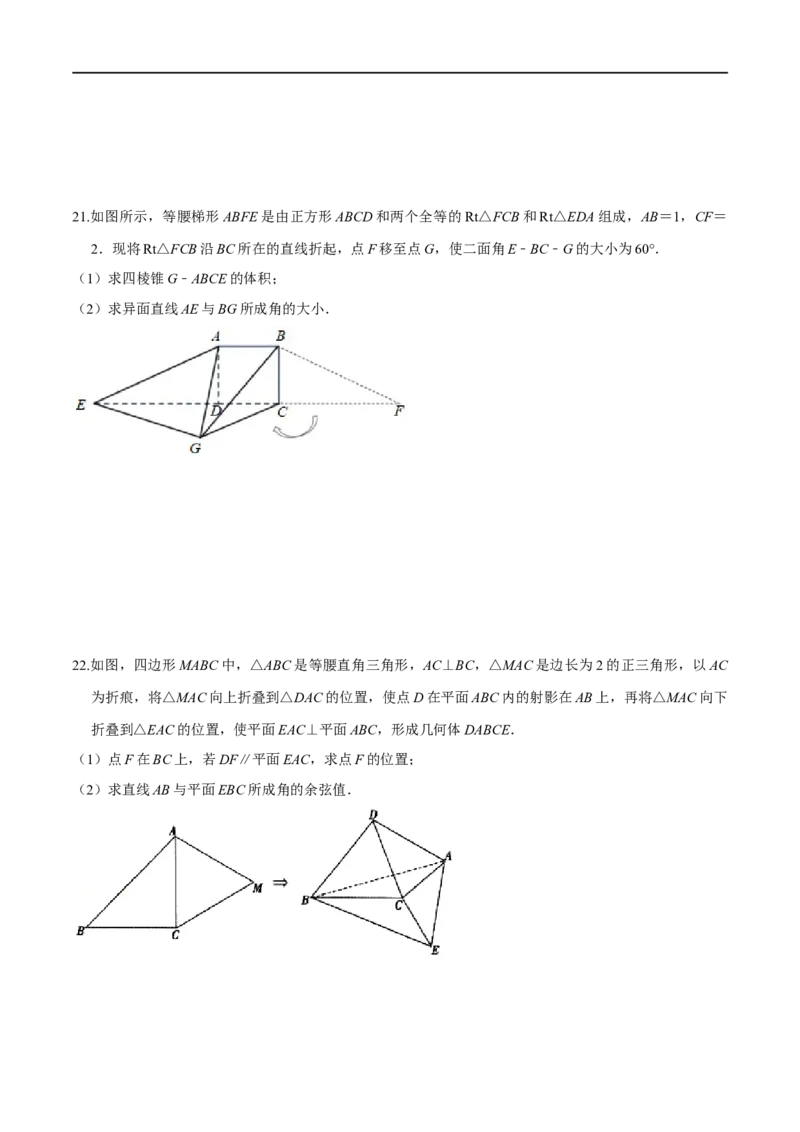
(Ⅱ)求平行四边形ABCD的面积.21.如图所示,等腰梯形ABFE是由正方形ABCD和两个全等的Rt△FCB和Rt△EDA组成,AB=1,CF=
2.现将Rt△FCB沿BC所在的直线折起,点F移至点G,使二面角E﹣BC﹣G的大小为60°.
(1)求四棱锥G﹣ABCE的体积;
(2)求异面直线AE与BG所成角的大小.
22.如图,四边形MABC中,△ABC是等腰直角三角形,AC⊥BC,△MAC是边长为2的正三角形,以AC
为折痕,将△MAC向上折叠到△DAC的位置,使点D在平面ABC内的射影在AB上,再将△MAC向下
折叠到△EAC的位置,使平面EAC⊥平面ABC,形成几何体DABCE.
(1)点F在BC上,若DF∥平面EAC,求点F的位置;
(2)求直线AB与平面EBC所成角的余弦值.