文档内容
高二年级下学期期末仿真卷 02
本试卷共22题。全卷满分150分。考试用时120分钟。
注意事项:
1.答卷前,考生务必将自己的姓名、考生号等填写在答题卡和试卷指定位置上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡对应题目的答案标号涂黑。如需改动,用橡
皮擦干净后,再选涂其他答案标号。回答非选择题时,将答案写在答题卡上。写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
一、选择题:本题共8小题,每小题5分,共40分。在每小题给出的四个选项中,只有一项是符合题目要
求的。
1.已知各项为正数的等比数列{a}中,a=1,aa=64,则公比q=( )
n 2 4 6
A.4 B.3 C.2 D.
2.从4种不同的书中买3本送给3名同学,每人各1本,不同的送法共有( )
A.4种 B.12种 C.24种 D.64种
3.直线 与曲线 相切,则b的值为( )
A.﹣2 B.﹣1 C. D.1
4.若函数f(x)=alnx﹣x2+5x在(1,3)内无极值点,则实数a的取值范围是( )
A.(﹣ ,3) B.(﹣∞,﹣ )
C.[3,+∞) D.(﹣∞,﹣ ]∪[3,+∞)
5.已知集合A={1,2,3,4},B={1,2,3,4,5},从集合A中任取3个不同的元素,其中最小的元素
用a表示,从集合B中任取3个不同的元素,其中最大的元素用b表示,记X=b﹣a,则随机变量X的
期望为( )
A. B. C.3 D.4
6.在二项式(x﹣2y)6的展开式中,设二项式系数和为A,各项系数和为B,x的奇次幂项的系数和为C,
则 =( )A.﹣ B. C.﹣ D.
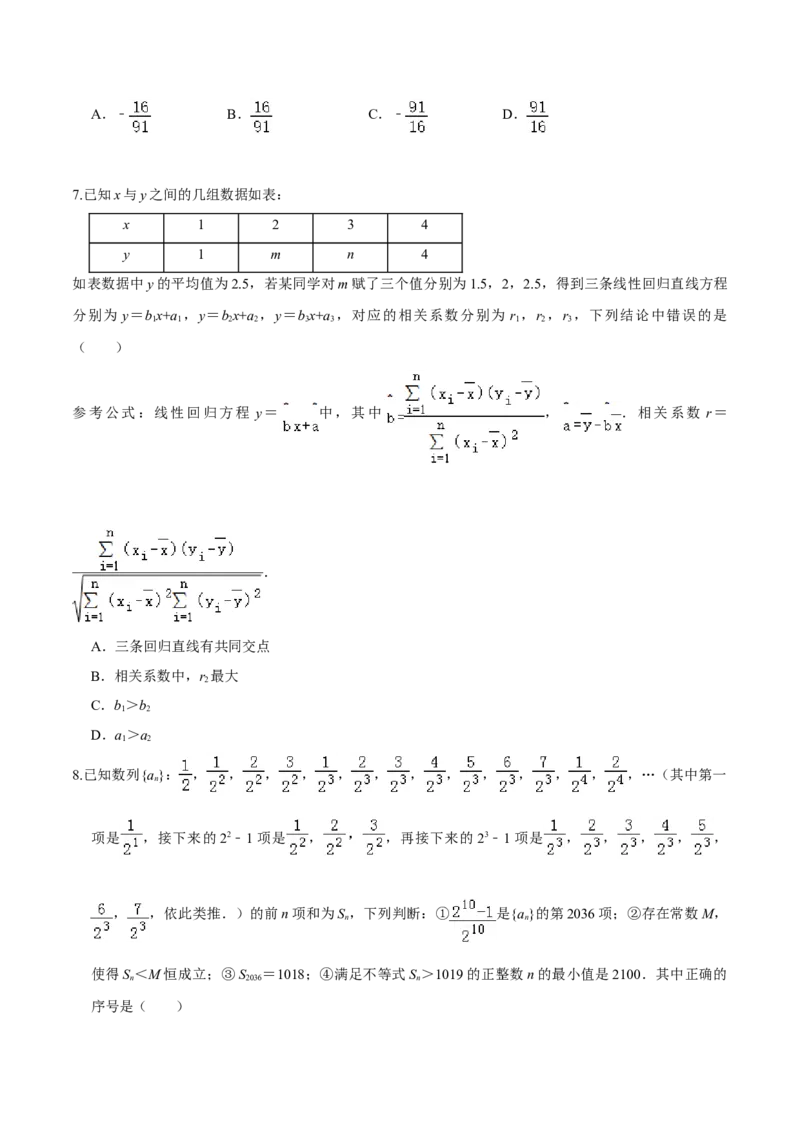
7.已知x与y之间的几组数据如表:
x 1 2 3 4
y 1 m n 4
如表数据中y的平均值为2.5,若某同学对m赋了三个值分别为1.5,2,2.5,得到三条线性回归直线方程
分别为 y=bx+a ,y=bx+a ,y=bx+a ,对应的相关系数分别为 r ,r ,r ,下列结论中错误的是
1 1 2 2 3 3 1 2 3
( )
参考公式:线性回归方程 y= 中,其中 , .相关系数 r=
.
A.三条回归直线有共同交点
B.相关系数中,r 最大
2
C.b>b
1 2
D.a>a
1 2
8.已知数列{a}: , , , , , , , , , , , , ,…(其中第一
n
项是 ,接下来的22﹣1项是 , ,再接下来的23﹣1项是 , , , , ,
, ,依此类推.)的前n项和为S ,下列判断:① 是{a}的第2036项;②存在常数M,
n n
使得S <M恒成立;③S =1018;④满足不等式S >1019的正整数n的最小值是2100.其中正确的
n 2036 n
序号是( )A.①②③ B.①②④ C.①③④ D.②③④
二、多选题:本题共4小题,每小题5分,共20分。在每小题给出的四个选项中,有多项是符合题目要求
的,选对得分,错选或漏选不得分。
9.已知数列{a}是等差数列,其前n项和为S,满足a+3a=S,则下列四个选项中正确的有( )
n n 1 2 6
A.a=0 B.S =0 C.S 最小 D.S=S.
7 13 7 5 8
10.现有3个男生4个女生,若从中选取3个学生,则( )
A.选取的3个学生都是女生的不同选法共有4种
B.选取的3个学生恰有1个女生的不同选法共有24种
C.选取的3个学生至少有1个女生的不同选法共有34种
D.选取的3个学生至多有1个男生的不同选法共有18种
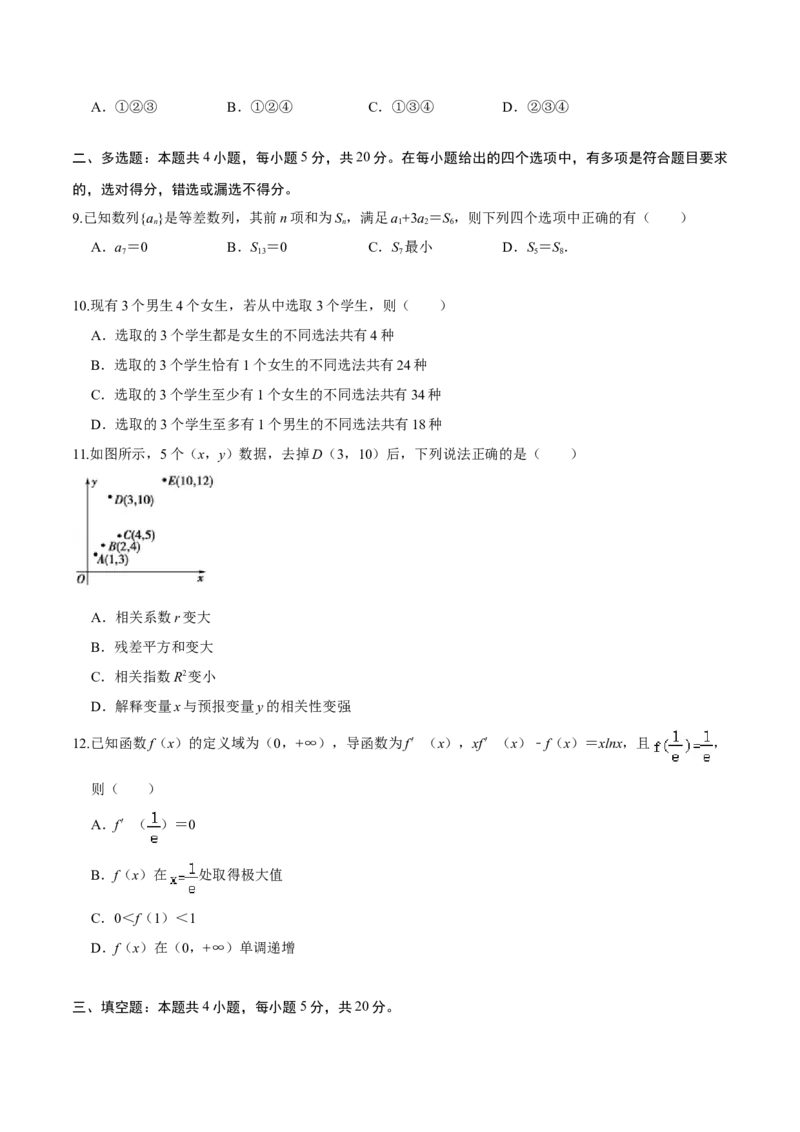
11.如图所示,5个(x,y)数据,去掉D(3,10)后,下列说法正确的是( )
A.相关系数r变大
B.残差平方和变大
C.相关指数R2变小
D.解释变量x与预报变量y的相关性变强
12.已知函数f(x)的定义域为(0,+∞),导函数为f′(x),xf′(x)﹣f(x)=xlnx,且 ,
则( )
A.f′( )=0
B.f(x)在 处取得极大值
C.0<f(1)<1
D.f(x)在(0,+∞)单调递增
三、填空题:本题共4小题,每小题5分,共20分。13.函数f(x)=(2x﹣x2)ex取得极小值时的x值为 .
14.已知(x﹣ )(1﹣x)4的展开式中x2的系数为4,则a= ,(x﹣ )(1﹣x)4的展开式中的常数
项为 .
15.用数学归纳法证明(n+1)(n+2)(n+3)…(n+n)=2n•1•3•5…(2n﹣1)(n N*)时,从n=k到n
=k+1时左边需增乘的代数式是 . ∈
16.已知一袋中有标有号码1、2、3、4的卡片各一张,每次从中取出一张,记下号码后放回,当四种号码
的卡片全部取出时即停止,则恰好取6次卡片时停止的概率为 .
四、解答题:共70分。解答应写出文字说明、证明过程或演算步骤。考生根据要求作答。
17.已知F(x)= t(t﹣4)dt,x (﹣1,+∞).
∈
(1)求F(x)的单调区间;
(2)求函数F(x)在[1,5]上的最值.
18.某校寒假行政值班安排,要求每天安排一名行政人员值日,现从包含甲、乙两人的七名行政人员中选四
人负责四天的轮班值日,在下列条件下,各有多少种不同的安排方法?
(1)甲、乙两人都被选中,且安排在前两天值日;
(2)甲、乙两人只有一人被选中,且不能安排在后两天值日.19.已知 的展开式中第2项与第3项的二项式系数之比是1:3.
(1)求n的值;
(2)求二项展开式中各项二项式系数和以及各项系数和;
(3)求展开式中系数的绝对值最大的项.
20.近年来,随着全球石油资源紧张、大气污染日益严重和电池技术的提高,电动汽车已被世界公认为 21
世纪汽车工业改造和发展的主要方向.为了降低对大气的污染和能源的消耗,某品牌汽车制造商研发了
两款电动汽车车型A和车型B,并在黄金周期间同时投放市场.为了了解这两款车型在黄金周的销售情
况,制造商随机调查了5家汽车4S店的销量(单位:台),得到如表:
4S店 甲 乙 丙 丁 戊
车型A 6 6 13 8 1l
车型B 12 9 13 6 4
(Ⅰ)若从甲、乙两家4S店销售出的电动汽车中分别各自随机抽取1台电动汽车作满意度调查,求抽取的
2台电动汽车中至少有1台是车型A的概率;
(Ⅱ)现从这5家汽车4S店中任选3家举行促销活动,用X表示其中车型A销量超过车型B销量的4S店
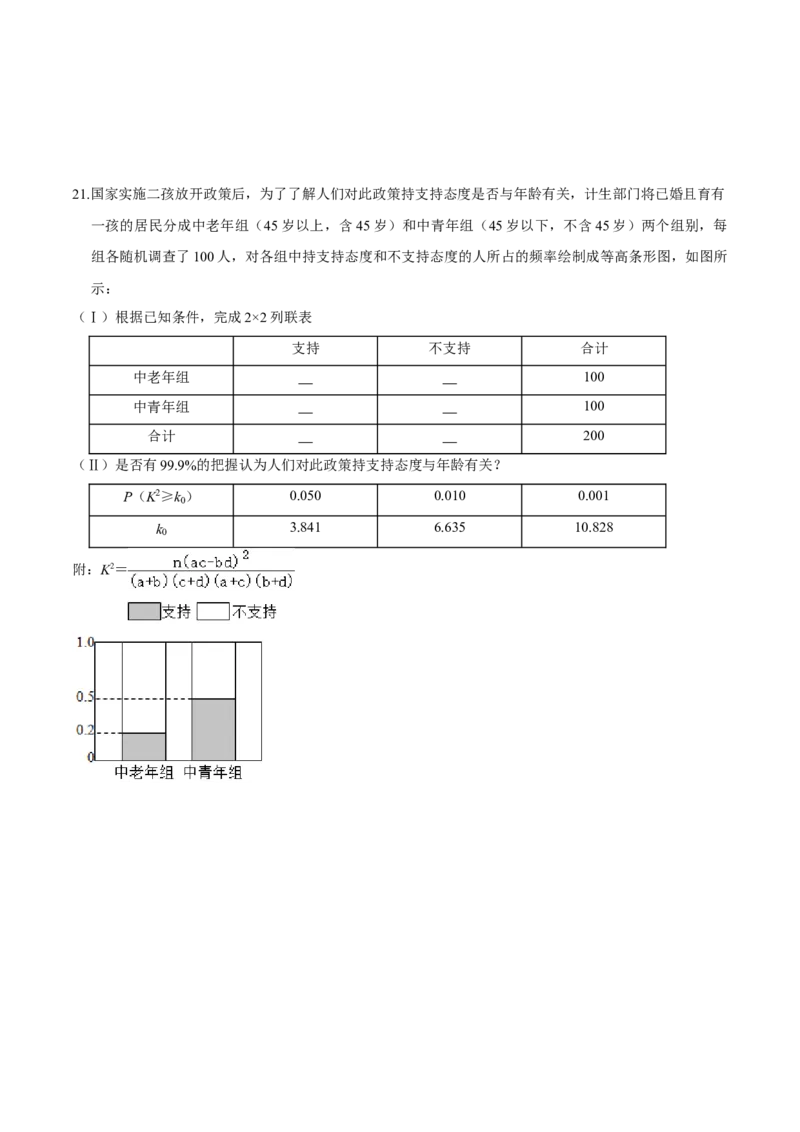
的个数,求随机变量X的分布列和数学期望.21.国家实施二孩放开政策后,为了了解人们对此政策持支持态度是否与年龄有关,计生部门将已婚且育有
一孩的居民分成中老年组(45岁以上,含45岁)和中青年组(45岁以下,不含45岁)两个组别,每
组各随机调查了100人,对各组中持支持态度和不支持态度的人所占的频率绘制成等高条形图,如图所
示:
(Ⅰ)根据已知条件,完成2×2列联表
支持 不支持 合计
中老年组 100
中青年组 100
合计 200
(Ⅱ)是否有99.9%的把握认为人们对此政策持支持态度与年龄有关?
P(K2≥k ) 0.050 0.010 0.001
0
k 3.841 6.635 10.828
0
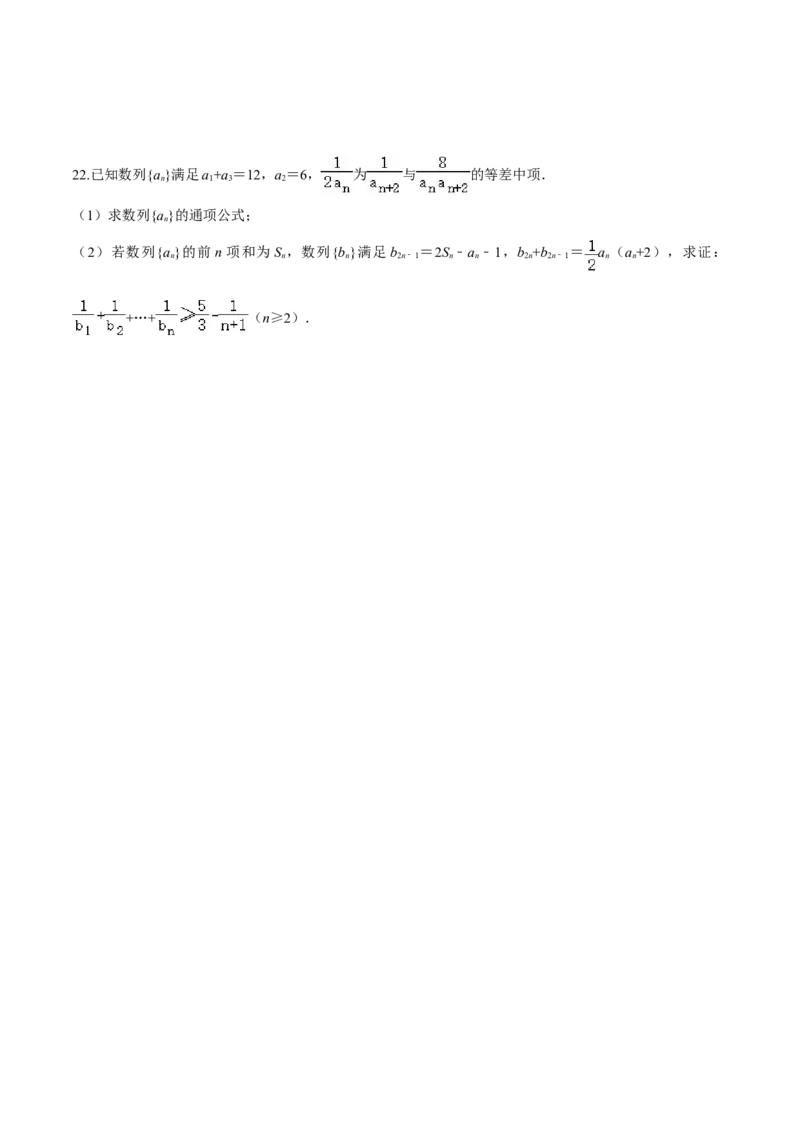
附:K2=22.已知数列{a}满足a+a=12,a=6, 为 与 的等差中项.
n 1 3 2
(1)求数列{a}的通项公式;
n
(2)若数列{a}的前n项和为S ,数列{b}满足b =2S﹣a﹣1,b +b = a (a+2),求证:
n n n 2n﹣1 n n 2n 2n﹣1 n n
+…+ (n≥2).