文档内容
期中检测卷 03
姓名:__________________ 班级:______________ 得分:_________________
注意事项:
本试卷满分150分,考试时间120分钟,试题共22题.答卷前,考生务必用0.5毫米黑色签字笔将自
己的姓名、班级等信息填写在试卷规定的位置.
一、选择题(本大题共8小题,每小题5分,共40分)在每小题所给出的四个选项中,只有一项是符合题
目要求的.
1.已知向量 =(x,2), =(1,﹣1),且 ∥ ,则 • =( )
A.4 B.2 C.0 D.﹣4
2.已知复数z=(2+i)i,其中i为虚数单位,则下列说法中,错误的是( )
A.|z|<3
B.z的虚部为2
C.z的共扼复数为2i+1
D.z在复平面内对应的点在第二象限
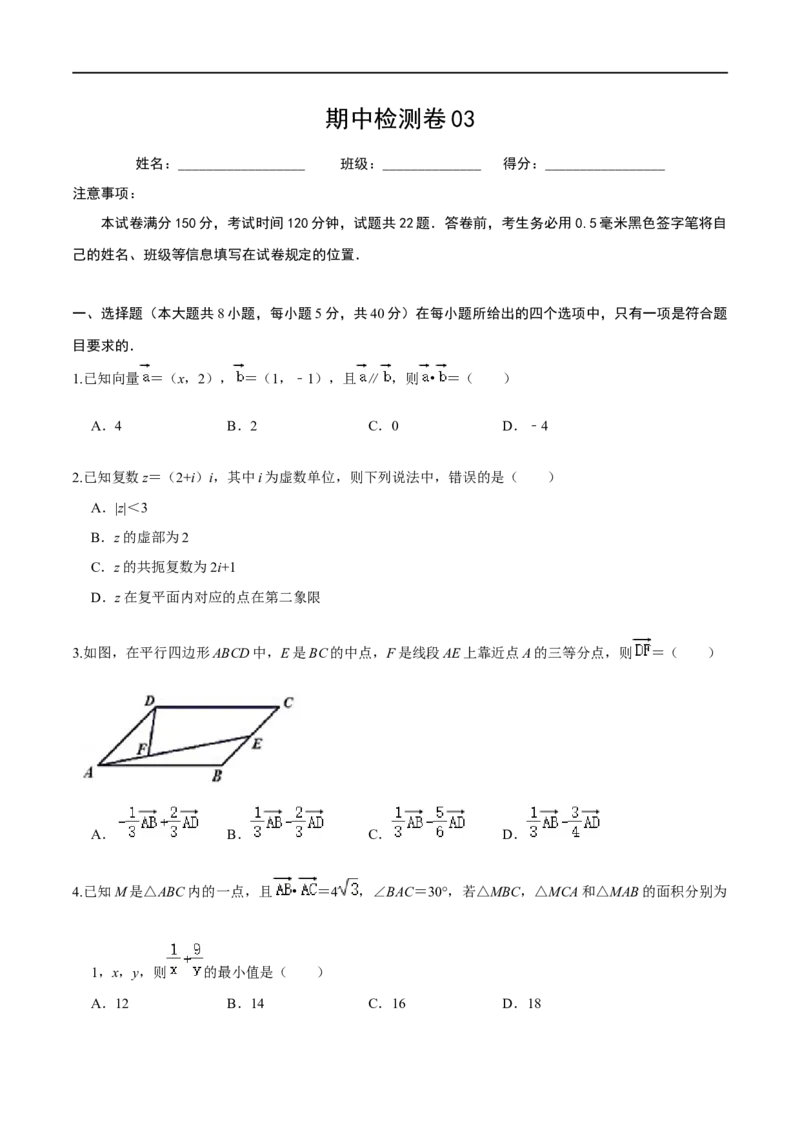
3.如图,在平行四边形ABCD中,E是BC的中点,F是线段AE上靠近点A的三等分点,则 =( )
A. B. C. D.
4.已知M是△ABC内的一点,且 • =4 ,∠BAC=30°,若△MBC,△MCA和△MAB的面积分别为
1,x,y,则 的最小值是( )
A.12 B.14 C.16 D.185.定义复数的一种运算z*z = (等式右边为普通运算),若复数z=a+bi,且正实数a,b满
1 2
足a+b=3,则z* 最小值为( )
A. B. C. D.
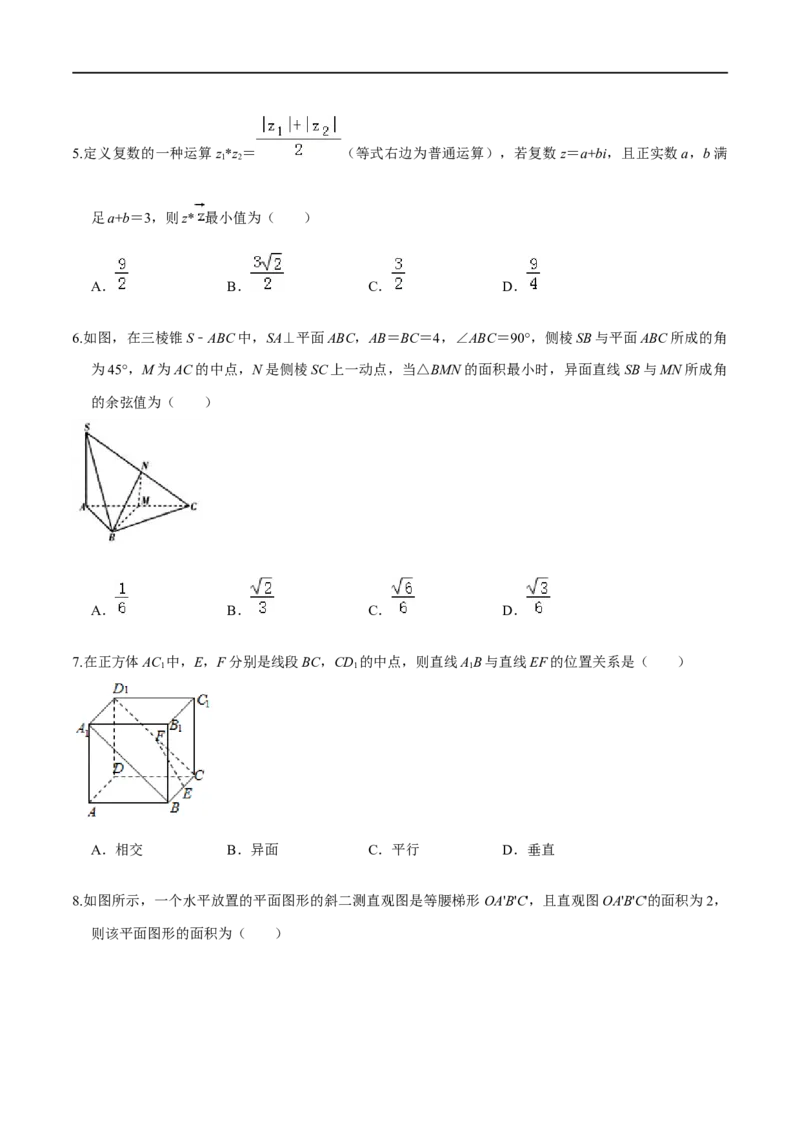
6.如图,在三棱锥S﹣ABC中,SA⊥平面ABC,AB=BC=4,∠ABC=90°,侧棱SB与平面ABC所成的角
为45°,M为AC的中点,N是侧棱SC上一动点,当△BMN的面积最小时,异面直线SB与MN所成角
的余弦值为( )
A. B. C. D.
7.在正方体AC 中,E,F分别是线段BC,CD 的中点,则直线AB与直线EF的位置关系是( )
1 1 1
A.相交 B.异面 C.平行 D.垂直
8.如图所示,一个水平放置的平面图形的斜二测直观图是等腰梯形 OA'B'C',且直观图OA'B'C'的面积为2,
则该平面图形的面积为( )A.2 B.4 C.4 D.2
二、多选题(本大题共4小题,每小题5分,选对得分,选错、少选不得分)
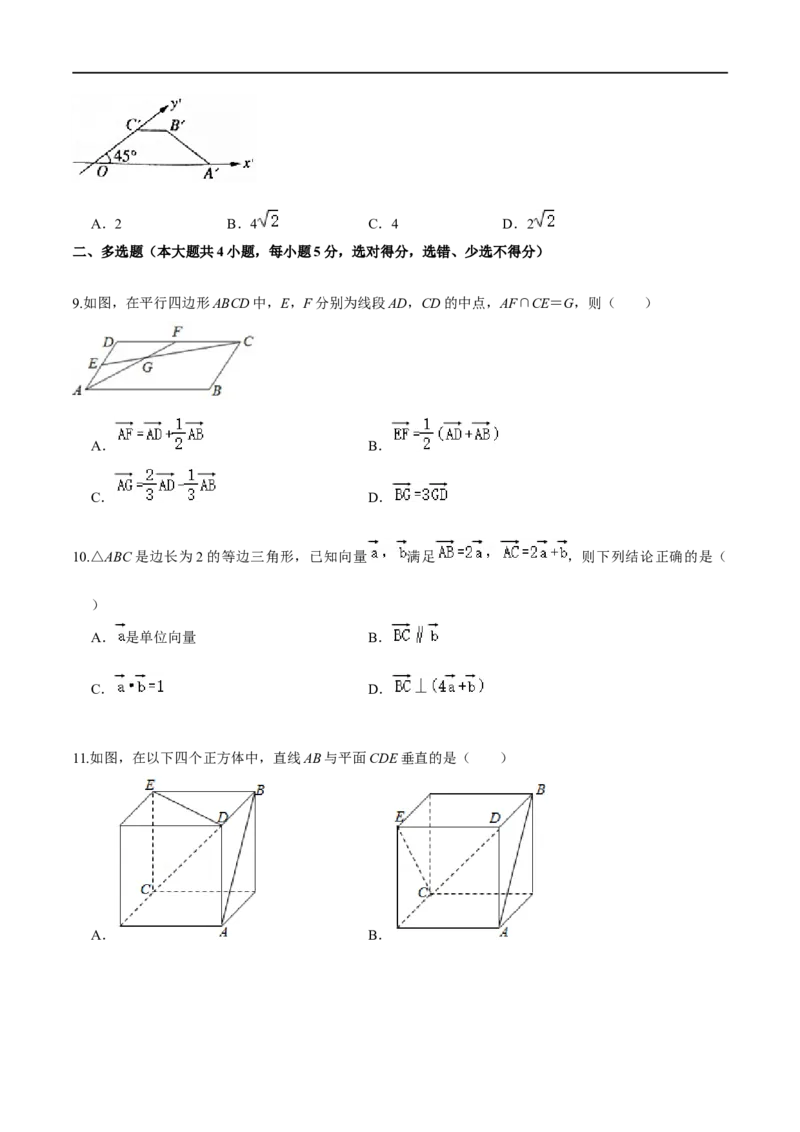
9.如图,在平行四边形ABCD中,E,F分别为线段AD,CD的中点,AF∩CE=G,则( )
A. B.
C. D.
10.△ABC是边长为2的等边三角形,已知向量 满足 ,则下列结论正确的是(
)
A. 是单位向量 B.
C. D.
11.如图,在以下四个正方体中,直线AB与平面CDE垂直的是( )
A. B.C. D.
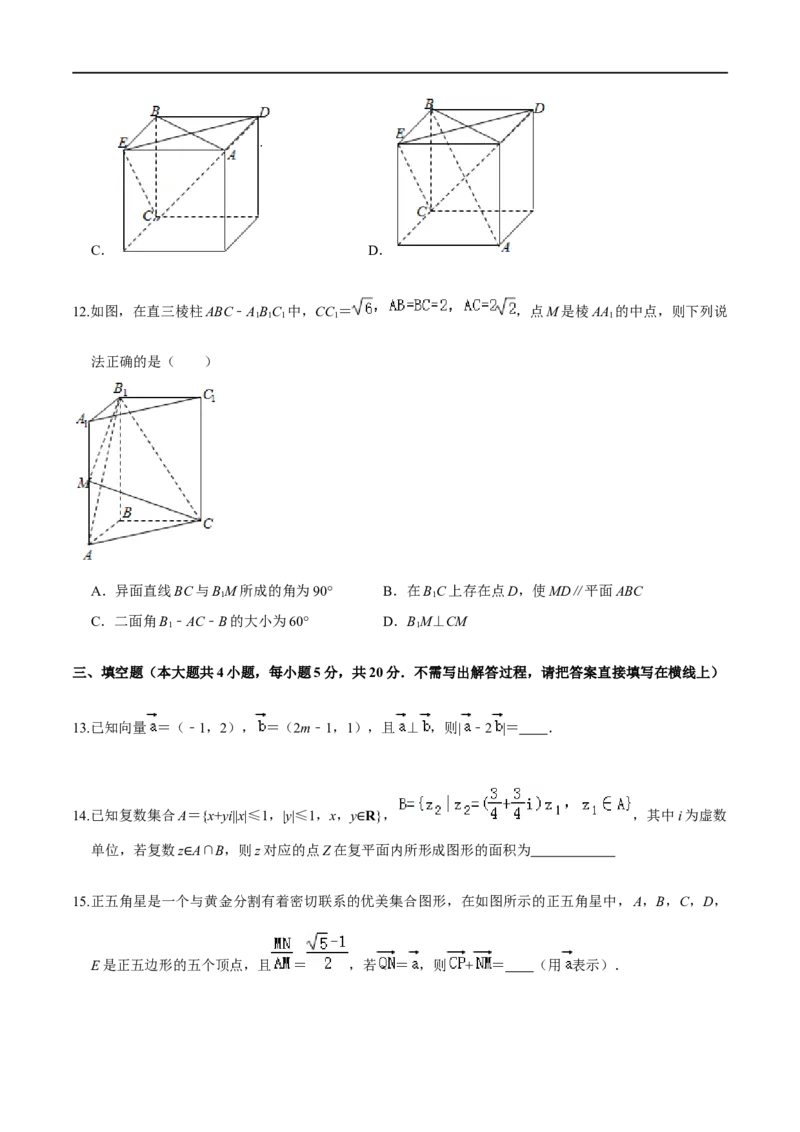
12.如图,在直三棱柱ABC﹣ABC 中,CC = ,点M是棱AA 的中点,则下列说
1 1 1 1 1
法正确的是( )
A.异面直线BC与BM所成的角为90° B.在BC上存在点D,使MD∥平面ABC
1 1
C.二面角B﹣AC﹣B的大小为60° D.BM⊥CM
1 1
三、填空题(本大题共4小题,每小题5分,共20分.不需写出解答过程,请把答案直接填写在横线上)
13.已知向量 =(﹣1,2), =(2m﹣1,1),且 ⊥ ,则| ﹣2 |= .
14.已知复数集合A={x+yi||x|≤1,|y|≤1,x,y R}, ,其中i为虚数
单位,若复数z A∩B,则z对应的点Z在复∈平面内所形成图形的面积为
∈
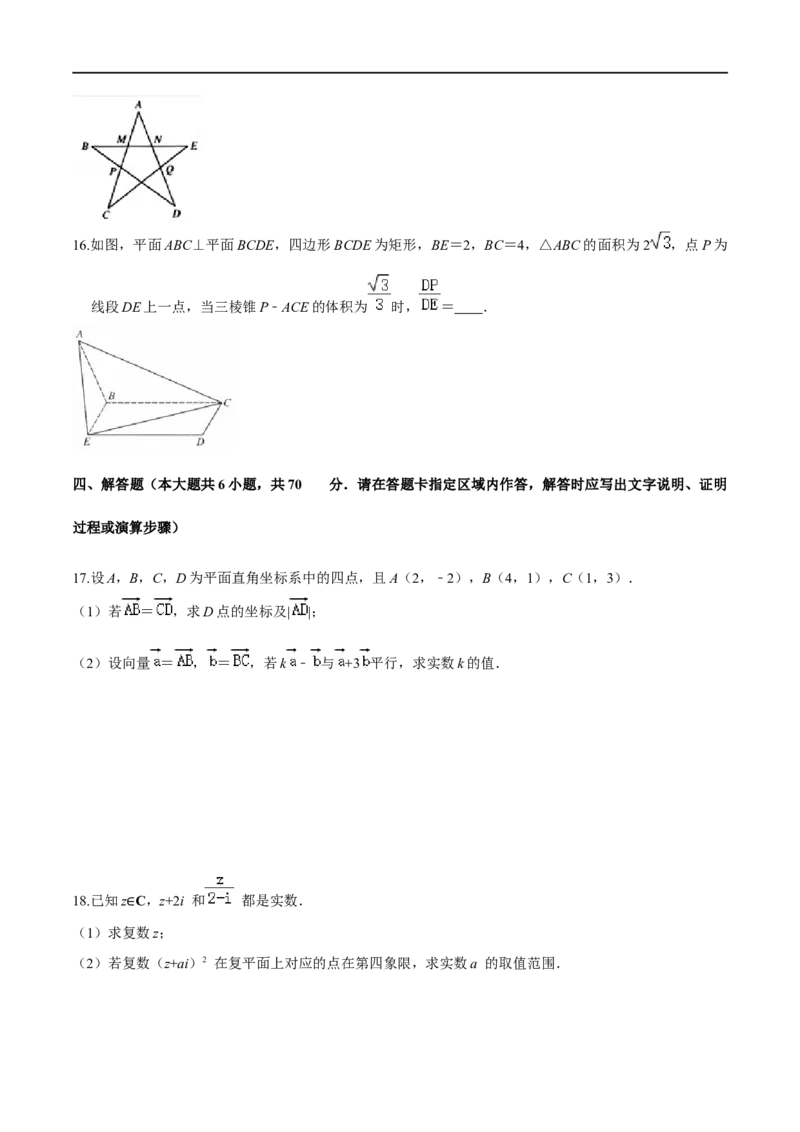
15.正五角星是一个与黄金分割有着密切联系的优美集合图形,在如图所示的正五角星中,A,B,C,D,
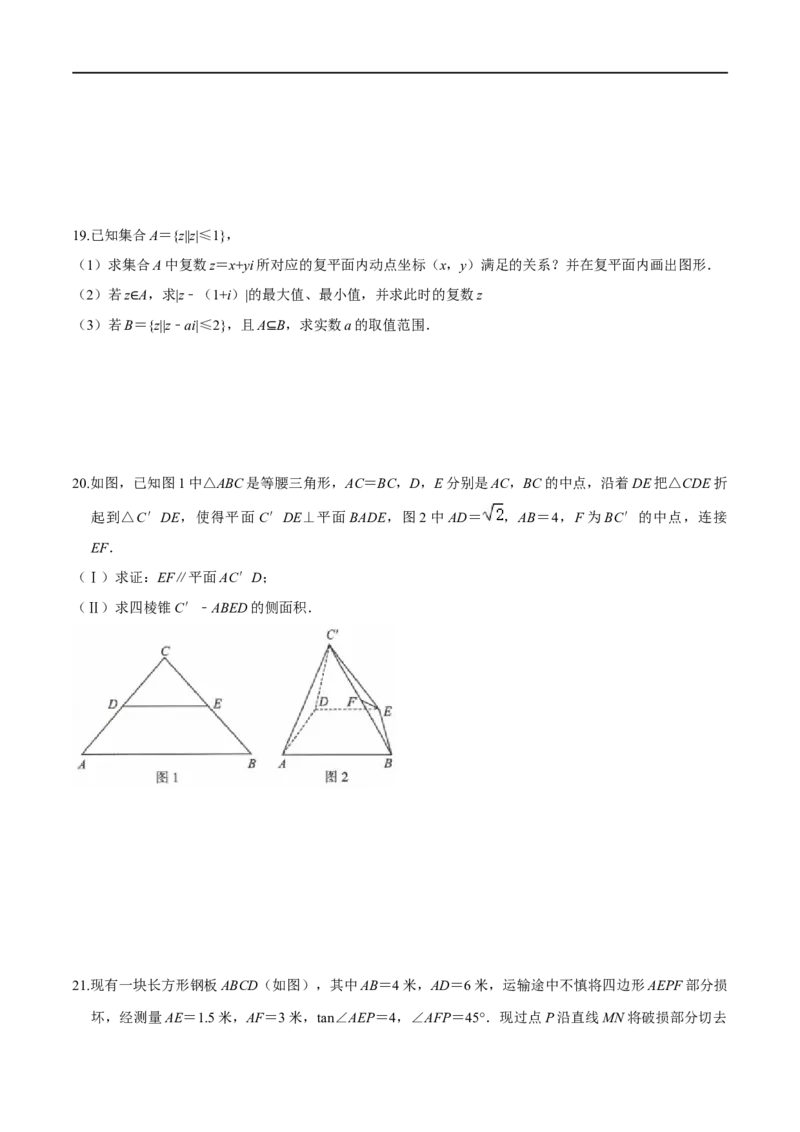
E是正五边形的五个顶点,且 = ,若 = ,则 + = (用 表示).16.如图,平面ABC⊥平面BCDE,四边形BCDE为矩形,BE=2,BC=4,△ABC的面积为2 ,点P为
线段DE上一点,当三棱锥P﹣ACE的体积为 时, = .
四、解答题(本大题共6小题,共70 分.请在答题卡指定区域内作答,解答时应写出文字说明、证明
过程或演算步骤)
17.设A,B,C,D为平面直角坐标系中的四点,且A(2,﹣2),B(4,1),C(1,3).
(1)若 = ,求D点的坐标及| |;
(2)设向量 = , = ,若k ﹣ 与 +3 平行,求实数k的值.
18.已知z C,z+2i 和 都是实数.
(1)求复∈数z;
(2)若复数(z+ai)2 在复平面上对应的点在第四象限,求实数a 的取值范围.19.已知集合A={z||z|≤1},
(1)求集合A中复数z=x+yi所对应的复平面内动点坐标(x,y)满足的关系?并在复平面内画出图形.
(2)若z A,求|z﹣(1+i)|的最大值、最小值,并求此时的复数z
(3)若B∈={z||z﹣ai|≤2},且A B,求实数a的取值范围.
⊆
20.如图,已知图1中△ABC是等腰三角形,AC=BC,D,E分别是AC,BC的中点,沿着DE把△CDE折
起到△C′DE,使得平面C′DE⊥平面BADE,图2中AD= ,AB=4,F为BC′的中点,连接
EF.
(Ⅰ)求证:EF∥平面AC′D;
(Ⅱ)求四棱锥C′﹣ABED的侧面积.
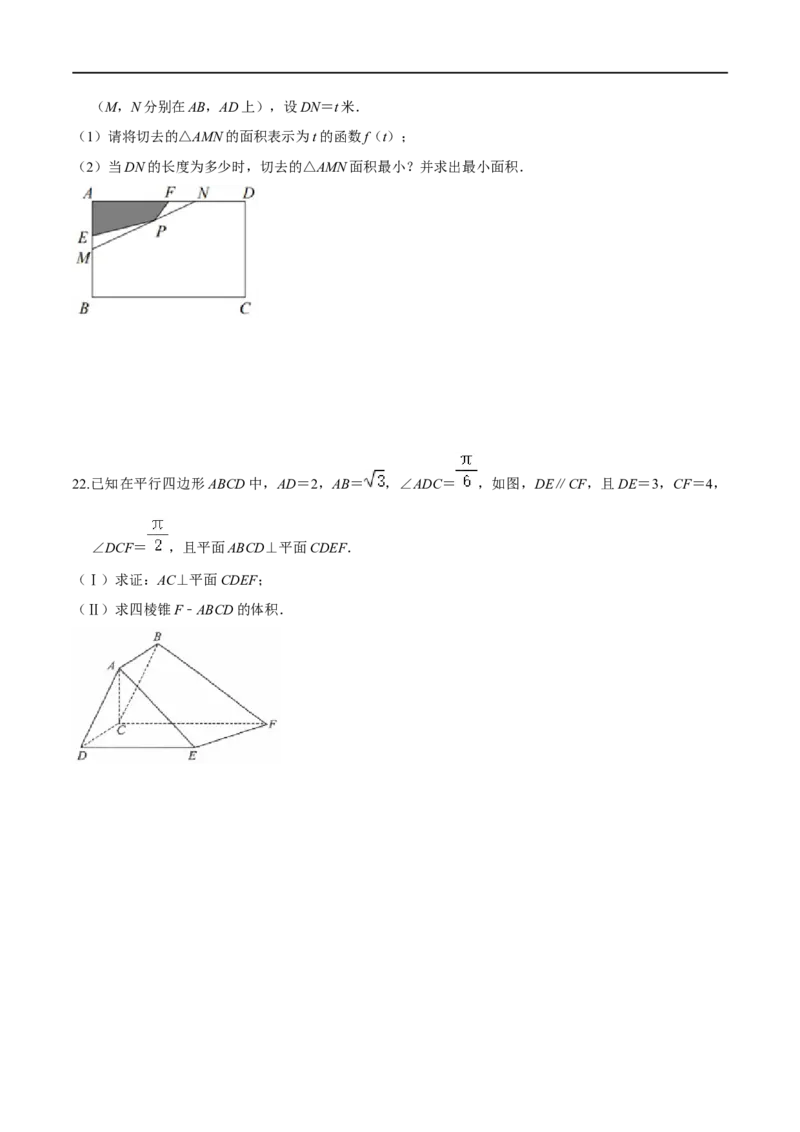
21.现有一块长方形钢板ABCD(如图),其中AB=4米,AD=6米,运输途中不慎将四边形AEPF部分损
坏,经测量AE=1.5米,AF=3米,tan∠AEP=4,∠AFP=45°.现过点P沿直线MN将破损部分切去(M,N分别在AB,AD上),设DN=t米.
(1)请将切去的△AMN的面积表示为t的函数f(t);
(2)当DN的长度为多少时,切去的△AMN面积最小?并求出最小面积.
22.已知在平行四边形ABCD中,AD=2,AB= ,∠ADC= ,如图,DE∥CF,且DE=3,CF=4,
∠DCF= ,且平面ABCD⊥平面CDEF.
(Ⅰ)求证:AC⊥平面CDEF;
(Ⅱ)求四棱锥F﹣ABCD的体积.