文档内容
高二年级下学期期末仿真卷 03
本试卷共22题。全卷满分150分。考试用时120分钟。
注意事项:
1.答卷前,考生务必将自己的姓名、考生号等填写在答题卡和试卷指定位置上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡对应题目的答案标号涂黑。如需改动,用橡
皮擦干净后,再选涂其他答案标号。回答非选择题时,将答案写在答题卡上。写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
一、选择题:本题共8小题,每小题5分,共40分。在每小题给出的四个选项中,只有一项是符合题目要
求的。
1.在等比数列{a}中,aa=a=4,则a=( )
n 1 3 4 6
A.6 B.±8 C.﹣8 D.8
【答案】D
【分析】利用等比数列的通项公式即可得出.
【解答】解:设等比数列{a}的公比为q,∵aa=a=4,∴ =4,
n 1 3 4
解得a=q=± ,
1
则a= =8.
6
故选:D.
【知识点】等比数列的通项公式
2.已知函数f(x)的导函数为f′(x),且满足关系式f(x)=x2+3xf′(2)+lnx,则f′(2)的值等于(
)
A.2 B.﹣2 C. D.
【答案】D
【分析】对等式f(x)=x2+3xf′(2)+lnx,求导数,然后令x=2,即可求出f′(2)的值.
【解答】解:∵f(x)=x2+3xf′(2)+lnx,
∴f′(x)=2x+3f′(2)+ ,
令x=2,则f′(2)=4+3f′(2)+ ,
即2f′(2)=﹣ ,
∴f′(2)=﹣ .
故选:D.【知识点】导数的加法与减法法则
3.数列a,a,…,a 中,恰好有6个7,3个4,则不相同的数列共有( )个
1 2 9
A. B. C. D.
【答案】C
【分析】根据题意,分析可得原问题可以转化为“先在a ,a ,…,a 中,任选3个安排“4”,剩下的6
1 2 9
个安排6个“7””的问题,由组合式公式分析可得答案.
【解答】解:根据题意,数列a,a,…,a 中,恰好有6个7,3个4,
1 2 9
可以先在a,a,…,a 中,任选3个安排“4”,剩下的6个安排6个“7”,
1 2 9
则有C 3种不同的情况,即可以有C 3个不相同的数列;
9 9
故选:C.
【知识点】排列、组合及简单计数问题
4.我国古代数学著作(算法统宗》中有这样一个问题(意为):“有一个人要走 378里路,第一天健步行
走,从第二天起因脚痛每天走的路程为前一天的一半,走了 6天后到达目的地.“那么,此人第4天和
第5天共走路程是( )
A.24里 B.36里 C.48里 D.60里
【答案】B
【分析】记每天走的路程里数为{a},可知{a}是公比q= 的等比数列,由S =378,得S =
n n 6 6
=378,解得:a,利用通项公式可得a+a.
1 4 5
【解答】解:记每天走的路程里数为{a},可知{a}是公比q= 的等比数列,
n n
由S=378,得S= =378,解得:a=192,
6 6 1
∴a+a= +192× =24+12=36.
4 5
此人第4天和第5天共走了24+12=36里.
故选:B.
【知识点】等差数列的前n项和
5.函数 (x [﹣ , ])的图象大致是( )
∈ π π
A. B.C. D.
【答案】B
【分析】利用函数的奇偶性排除选项,通过函数的特殊点的位置判断即可.
【解答】解:函数 (x [﹣ , ])是奇函数,排除选项A、C,
当0<x≤ 时,f(x)=﹣xecosx,f∈′(πx)=π ﹣ecosx(1+xsinx),
存在x (0, ),1+xsinx=0时,当x (0,x)时,f′(x)<0,函数是减函数,
0 0 0 0
π
x (x, ),f′(x)>0,函数是增函数,排除D.
0
∈ π ∈
故选:B.
∈ π
【知识点】函数的图象与图象的变换、利用导数研究函数的单调性
6.若直线x+ay﹣1=0与2x﹣4y+3=0垂直,则二项式 的展开式中x的系数为( )
A.﹣2 B. C.2 D.
【答案】B
【分析】利用两条直线垂直的性质求得a的值,再利用二项展开式的通项公式,求得展开式中x的系数.
【解答】解:由直线直线x+ay﹣1=0与2x﹣4y+3=0垂直,可得1×2+a×(﹣4)=0,求得a= ,
则二项式 = 的展开式的通项公式为T = • •(﹣1)r•x10﹣
r+1
3r,
令10﹣3r=1,求得r=3,可得展开式中x的系数为 • •(﹣1)=﹣ ,
故选:B.
【知识点】直线的一般式方程与直线的垂直关系、二项式定理
7.已知随机变量 满足E(1﹣ )=5,D(1﹣ )=5,则下列说法正确的是( )
A.E( )=η﹣5,D( )=η 5 ηB.E( )=﹣4,D( )=﹣4
C.E(η)=﹣5,D(η)=﹣5 D.E(η)=﹣4,D(η)=5
【答案】Dη η η η
【分析】随机变量 满足E(1﹣ )=5,D(1﹣ )=5,可得1﹣E =5,D =5,解出即可得出.
【解答】解:∵随机变量 满足E(1﹣ )=5,D(1﹣ )=5,
η η η η η
∴1﹣E =5,D =5,
η η η
解得E =﹣4,D =5,
η η
故选:D.
η η
【知识点】离散型随机变量的期望与方差
8.已知具有线性相关的两个变量x,y之间的一组数据如表所示:x 0 1 2 3 4
y 2.2 4.3 4.5 4.8 6.7
若x,y满足回归方程 ,则以下为真命题的是( )
A.x每增加1个单位长度,则y一定增加1.5个单位长度
B.x每增加1个单位长度,y就减少1.5个单位长度
C.所有样本点的中心为(1,4.5)
D.当x=8时,y的预测值为13.5
【答案】D
【分析】计算出 =2, =4.5,后可得 =1.5,可得回归方程,根据回归方程可得D正确.
【解答】解:∵ = =2, = =4.5,∴C错误;
∴ = ﹣1.5× =4.5﹣1.5×2=1.5,∴回归方程 =1.5x+1.5,
当x每增加一个单位时,y的预测值增加1.5个单位长度不是一定增加1.5个单位长度,所以A
不正确,B不正确;
x=8时,y的预测值为13.5,D正确.
故选:D.
【知识点】线性回归方程
二、多选题:本题共4小题,每小题5分,共20分。在每小题给出的四个选项中,有多项是符合题目要求
的,选对得分,错选或漏选不得分。
9.若 ,则x的值为( )
A.4 B.6 C.9 D.18
【答案】AC
【分析】由 ,利用组合数的性质即可得出x=3x﹣8或x+3x﹣8=28,解出即可得出.
【解答】解:∵ ,
∴x=3x﹣8或x+3x﹣8=28,
解得:x=4,或9.
故选:AC.
【知识点】组合及组合数公式
10.已知函数f(x)=xln(1+x),则( )
A.f(x)在(0,+∞)单调递增
B.f(x)有两个零点C.曲线y=f(x)在点(﹣ ,f(﹣ ))处切线的斜率为﹣1﹣ln2
D.f(x)是偶函数
【答案】AC
【分析】先对函数求导,然后结合导数与单调性关系,导数的几何意义及函数性质分别检验各选项即可判
断.
【解答】解:函数定义域(﹣1,+∞),不关于原点对称,D错误,
因为 ,
当x<0时,f′(x)>0恒成立,f(x)单调递增,A正确,
= ,
当x>﹣1时,f″(x)>0,f′(x)单调递增且f′(0)=0,
故当x (﹣1,0)时,f′(x)<0,f(x)单调递减,当x (0,+∞)时,f′(x)>0,f
(x)单调递增,
∈ ∈
又f(0)=0,
所以f(x)只有一个零点,B正确,
因为f′(﹣ )=ln ﹣1=﹣1﹣ln2,C 正确.
故选:AC.
【知识点】导数及其几何意义、利用导数研究函数的单调性
11.下列关于公差d>0的等差数列{a}的四个命题中真命题是( )
n
A.数列{a}是递增数列;
n
B.数列{na}是递增数列;
n
C.数列 是递增数列;
D.数列{a+3nd}是递增数列;
n
【答案】AD
【分析】对于各个选项中的数列,计算第n+1项与第n项的差,看此差的符号,再根据递增数列的定义得
出结论.
【解答】解:∵对于公差d>0的等差数列{a},a ﹣a=d>0,∴数列{a}是递增数列成立,A是真命题.
n n+1 n n
对于数列{na},第n+1项与第n项的差等于 (n+1)a ﹣na =(n+1)d+a ,不一定是正实
n n+1 n n
数,B是假命题.
对于数列 ,第n+1项与第n项的差等于 ﹣ = = ,不
一定是正实数,C是假命题.
对于数列{a+3nd},第 n+1项与第 n项的差等于 a +3(n+1)d﹣a﹣3nd=4d>0,数列
n n+1 n
{a+3nd}是递增数列成立,D是真命题.
n
故选:AD.
【知识点】等差数列的性质
12.若随机变量X服从两点分布,其中 ,E(X)、D(X)分别为随机变量X均值与方差,则下列结论正确的是( )
A.P(X=1)=E(X) B.E(3X+2)=4
C.D(3X+2)=4 D.
【答案】AB
【分析】推丑陋同P(X=1)= 从而E(X)= ,D(X)=(0﹣ )2× +(1﹣ )2×
= ,由此能过河卒子同结果.
【解答】解:随机变量X服从两点分布,其中 ,
∴P(X=1)= ,
E(X)= ,
D(X)=(0﹣ )2× +(1﹣ )2× = ,
在A中,P(X=1)=E(X),故A正确;
在B中,E(3X+2)=3E(X)+2=3× =4,故B正确;
在C中,D(3X+2)=9D(X)=9× =2,故C错误;
在D中,D(X)= ,故D错误.
故选:AB.
【知识点】离散型随机变量的期望与方差
三、填空题:本题共4小题,每小题5分,共20分。
13.设等比数列{a}的公比为2,前10项和为S = ,则a 的值为 .
n 10 1
【分析】根据等比数列的前n项和公式建立方程进行求解即可.
【解答】解:由等比数列的前n项和公式得S = = ,
10
即1023a= ,即a= ,
1 1
故答案为:
【知识点】等比数列的前n项和
14.若函数y=x3﹣2x2+mx,当x= 时,函数取得极大值,则m的值为 .【答案】1
【分析】先求导,再利用导数与极值的关系求出m.
【解答】解:y′=3x2﹣4x+m,
∵当x= 时,函数取得极大值,
∴3× ﹣4× +m=0,
即 ﹣ +m=0,
即m﹣1=0.
∴m=1.
故答案为:1.
【知识点】利用导数研究函数的极值
15.已知x、y取值如表:
x 0 1 4 5 6
y 1.3 m 3m 5.6 7.4
画散点图分析可知:y与x线性相关,且求得回归方程为 =x+1,则m的值为 .(精确到0.1)
【答案】1.7
【分析】将 =3.2代入回归方程可得 =4.2,则4m=6.7,即可得出结论.
【解答】解:将 =3.2代入回归方程 =x+1可得 =4.2,
则4m=6.7,解得m=1.675,
即精确到0.1后m的值为1.7.
故答案为:1.7.
【知识点】线性回归方程
16.已知(x2﹣1)8=a+ax2+ax4+…+ax16,则a= ﹣ (结果用数字表示).
0 1 2 8 3
【答案】-56
【分析】由题意利用二项展开式的通项公式,求得a 的值.
3
【解答】解:∵(x2﹣1)8=a+ax2+ax4+…+ax16,展开式的通项公式为T = •x16﹣2r•(﹣1)r,令16﹣
0 1 2 8 r+1
2r=6,求得r=5,
则a= •(﹣1)3=﹣56,
3
故答案为:﹣56.
【知识点】二项式定理
四、解答题:共70分。解答应写出文字说明、证明过程或演算步骤。考生根据要求作答。
17.已知 (1+x)n的展开式中第4项和第8项的二项式系数相等.
(Ⅰ)求n的值和这两项的二项式系数;(Ⅱ)在 (1+x)3+(1+x)4+…+(1+x)n+2的展开式中,求含x2项的系数(结果用数字表示).
【分析】(Ⅰ)由二项式定理及二项式系数得:两项的二项式系数为 =120,
(Ⅱ)由二项式定理得:x2项的系数为 +…+ = =285,得解.
【解答】解:(Ⅰ)因为 ,
所以n=10,
所以 =120,
故两项的二项式系数120.
(Ⅱ)含x2项的系数为 +…+ = =285,
故答案为:285.
【知识点】二项式定理
18.已知函数f(x)= ,a R.
∈
(I)求函数f(x)的单调区间;
(Ⅱ)若f(x)在(1,2)上是单调函数,求a的取值范围.
【分析】(Ⅰ)根据题意,求出函数的定义域,求出函数的导数,对a的范围分3种情况讨论,分析导数
的符号,结合导数与函数单调性的关系分析可得每种情况下的单调区间,综合即可得答案;
(Ⅱ)由(Ⅰ)的结论,分3种情况讨论,求出a的范围,综合即可得答案.
【解答】解:(Ⅰ)函数f(x)= ,其定义域为{x|x≠a},其导数f′(x)= ,
分3种情况讨论:
①,a=0时,f(x)=x,(x≠0),函数的递增区间为(﹣∞,0)、(0,+∞);
②,a>0时,f′(x)= >0,解可得x>2a或x<0,反之f′(x)= <
0,解可得0<x<2a,且x≠a,
则函数f(x)的递增区间为(﹣∞,0)、(2a,+∞),
递减区间为(0,a)、(a,2a);
③,a<0时,f′(x)= >0,解可得x>0或x<2a,反之f′(x)= <
0,解可得2a<x<0,且x≠a,
则函数f(x)的递增区间为(﹣∞,2a)、(0,+∞),
递减区间为(2a,a)、(a,0);
综合可得:a=0时,函数的递增区间为(﹣∞,0)、(0,+∞);
a>0时,函数f(x)的递增区间为(﹣∞,0)、(2a,+∞),递减区间为(0,a)、(a,
2a);
a<0时,函数f(x)的递增区间为(﹣∞,2a)、(0,+∞),递减区间为(2a,a)、
(a,0);
(Ⅱ)根据题意,若f(x)在(1,2)上是单调函数,分3种情况讨论:
①,a=0时,函数f(x)的递增区间为(﹣∞,0)、(0,+∞),在区间(1,2)上是单调函数,符合题意;
②,a>0时,函数f(x)的递增区间为(﹣∞,0)、(2a,+∞),递减区间为(0,a)、
(a,2a);
若f(x)在(1,2)上是单调函数,则有(1,2)⊆(2a,+∞)或(1,2)⊆(0,a)或
(1,2)⊆(a,2a),
解可得:0<a≤ 或a=1或a≥2,
③,函数f(x)的递增区间为(﹣∞,2a)、(0,+∞),在区间(1,2)上是单调函数,符
合题意;
综合可得:a≤ 或a=1或a≥2.
【知识点】利用导数研究函数的单调性
19.某医疗专家组为了研究新冠肺炎病毒在特定环境下一周内随时间变化的繁殖情况,得到如下的实验数据:
天数t 1 2 3 4 5 6 7
(天)
繁殖个数y 1 1 2 3 4 4 6
(千个)
(1)由如表数据可知,可用线性回归模型拟合y与t的关系,求y关于t的线性回归方程;
(Ⅱ)若由线性回归方程得到的估计数据与实验数据的误差不超过 0.5,则该实验数据是“理想数据”,
现从实验数据中随机抽取3个,求“理想数据”的个数X的分布列和数学期望.
参考公式:回归方程 = t+ 中斜率和截距的最小二乘估计公式分别为 = , =
﹣ .
【分析】(Ⅰ)由表格中的数据及所给公式求得 与 的值,则线性回归方程可求;
(Ⅱ)根据表格将估计个数列出,求出“理想数据”的个数,写出 X的所有可能取值,再求出
相应的概率,写出分布列,求得期望.
【解答】解:(Ⅰ)由题意, , ,
, ,
∴ = ,.
∴y关于t的线性回归方程为 ;
(Ⅱ)由题意将估计数据与实验数据列表:
天 数 t 1 2 3 4 5 6 7
(天)
繁 殖 个 1 1 2 3 4 4 6
数
y(千个)
估 计 个 3
数
( 千
个)
由列表和题意可知该实验数据为“理想数据”的有5个,
故X的所有可能取值为1,2,3.
P(X=1)= ,
P(X=2)= ,
P(X=3)= .
∴“理想数据”个数X的分布列为:
X 1 2 3
P
则E(X)=1× .
【知识点】离散型随机变量的期望与方差、离散型随机变量及其分布列、线性回归方程
20.2019年9月1日央视《开学第一课》播出后,社会各界反响强烈,全国人民爱国主义热情空前高涨,在
新中国成立70周年前夕,上演了一次小高潮.某兴趣小组为了了解某校学生对《开学第一课》的喜欢
程度,从该校随机抽取了100名学生对该节目进行打分,并把相关的统计结果记录如表:
喜欢程度 不喜欢 喜欢 非常喜欢
分数段 [50,60) [60,70) [70,80) [80,90) [90,100]
频数 1 9 18 32 40
以喜欢程度位于各区间的频率代替喜欢程度位于该区间的概率.(1)试估计这100名学生对节目打分的中位数和平均数;
(2)为了感谢学生对该次调查统计的支持,兴趣小组决定从全校随机抽取3名学生进行奖励,X表示所抽
取的学生中来自“非常喜欢”的人数,求X的分布列和数学期望.
【分析】(1)将统计结果和频率分布直方图进行对比,用频率分布直方图估计中位数、平均数的方法进
行计算;
(2)先确定X的取值,再利用二项分布的概率计算公式求解概率,最后列出分布列,代入期
望公式求期望.
【解答】解:(1)∵0.01+0.09+0.18<0.5,0.01+0.09+0.18+0.32>0.5,
∴中位数x [80,90),
由0.01+0.0∈9+0.18+(x﹣80)× =0.5,解得x=86.875,
故中位数为86.875;
由55× +65× =85.1,
得平均数为85.1;
(2)从该校随机抽取1名学生,该学生对节目喜欢程度为“非常喜欢”的概率为 .
X的可能取值为0,1,2,3,
则P(X=0)= ,
P(X=1)= ,
P(X=2)= ,
P(X=3)= .
X的分布列为:
X 0 1 2 3
P
∴E(X)=0× = .
【知识点】离散型随机变量及其分布列、离散型随机变量的期望与方差
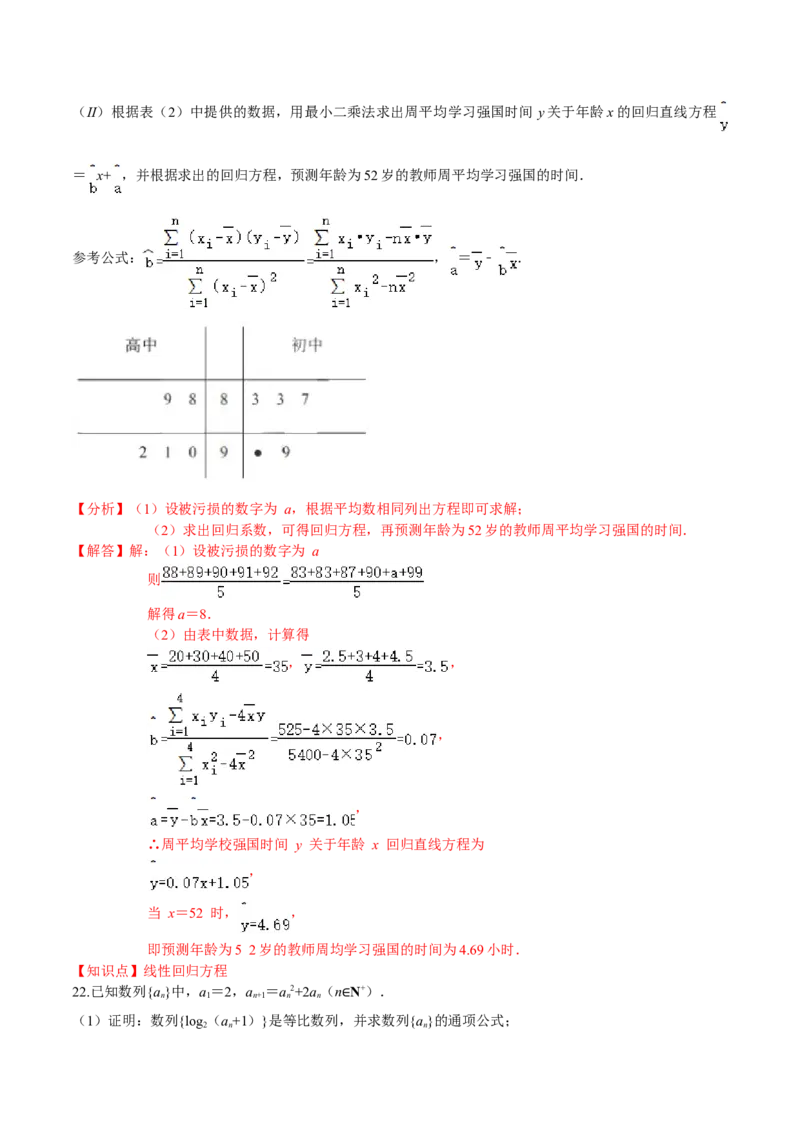
21.某市为了解中学教师学习强国的情况,调查了高中、初中各5所学校,根据教师学习强国人数的统计数
据(单位:人),画出如图茎叶图(其中一个数字被污损).并从学习强国的教师中随机抽取了4人,
统计了其学习强国的周平均时间(单位:小时)与年龄(单位:岁),并绘制了如图:
年龄 20 30 40 50
周平均学校强国时间 2.5 3 4 4.5
(I)若所调查的5所初中与5所高中学习强国的平均人数相同,求茎叶图中被污损的数字a;(II)根据表(2)中提供的数据,用最小二乘法求出周平均学习强国时间 y关于年龄x的回归直线方程
= x+ ,并根据求出的回归方程,预测年龄为52岁的教师周平均学习强国的时间.
参考公式: , = ﹣ .
【分析】(1)设被污损的数字为 a,根据平均数相同列出方程即可求解;
(2)求出回归系数,可得回归方程,再预测年龄为52岁的教师周平均学习强国的时间.
【解答】解:(1)设被污损的数字为 a
则
解得a=8.
(2)由表中数据,计算得
, ,
,
,
∴周平均学校强国时间 y 关于年龄 x 回归直线方程为
,
当 x=52 时, ,
即预测年龄为5 2岁的教师周均学习强国的时间为4.69小时.
【知识点】线性回归方程
22.已知数列{a}中,a=2,a =a2+2a(n N+).
n 1 n+1 n n
(1)证明:数列{log
2
(a
n
+1)}是等比数列,∈并求数列{a
n
}的通项公式;(2)记b= + ,求数列{b}的前n项和S.
n n n
【分析】(1)由已知得log (a +1)=log (a+1)2=2log (a+1),log (a+1)=log 3,由此能证明
2 n+1 2 n 2 n 2 1 2
数列{log (a+1)}是首项为log 3,公比为2的等比数列,从而求出 .
2 n 2
(2)由 a =a2+2a (n N+),两边取对数,得 ,从而 = ﹣
n+1 n n
∈
,进而b=2( ﹣ ),由此利用裂项求和法能求出数列{b}的前n项和S.
n n n
【解答】(1)证明:∵数列{a}中,a=2,a =a2+2a(n N+),
n 1 n+1 n n
∴a +1=a2+2a+1=(a+1)2,
n+1 n n n
∈
∴log (a +1)=log (a+1)2=2log (a+1),
2 n+1 2 n 2 n
∴ =2,
又log (a+1)=log 3,
2 1 2
∴数列{log (a+1)}是首项为log 3,公比为2的等比数列,
2 n 2
∴log (a+1)=log 3•2n﹣1,
2 n 2
∴ ,
∴ .
(2)解:∵a =a2+2a(n N+),
n+1 n n
两边取对数,得 ∈ ,
即 = ﹣ ,
∵b= + ,∴b=2( ﹣ ),
n n
∴S=2[( )+( )+…+( )]
n
=2( )
=1﹣ .
【知识点】数列的求和、等比数列的性质