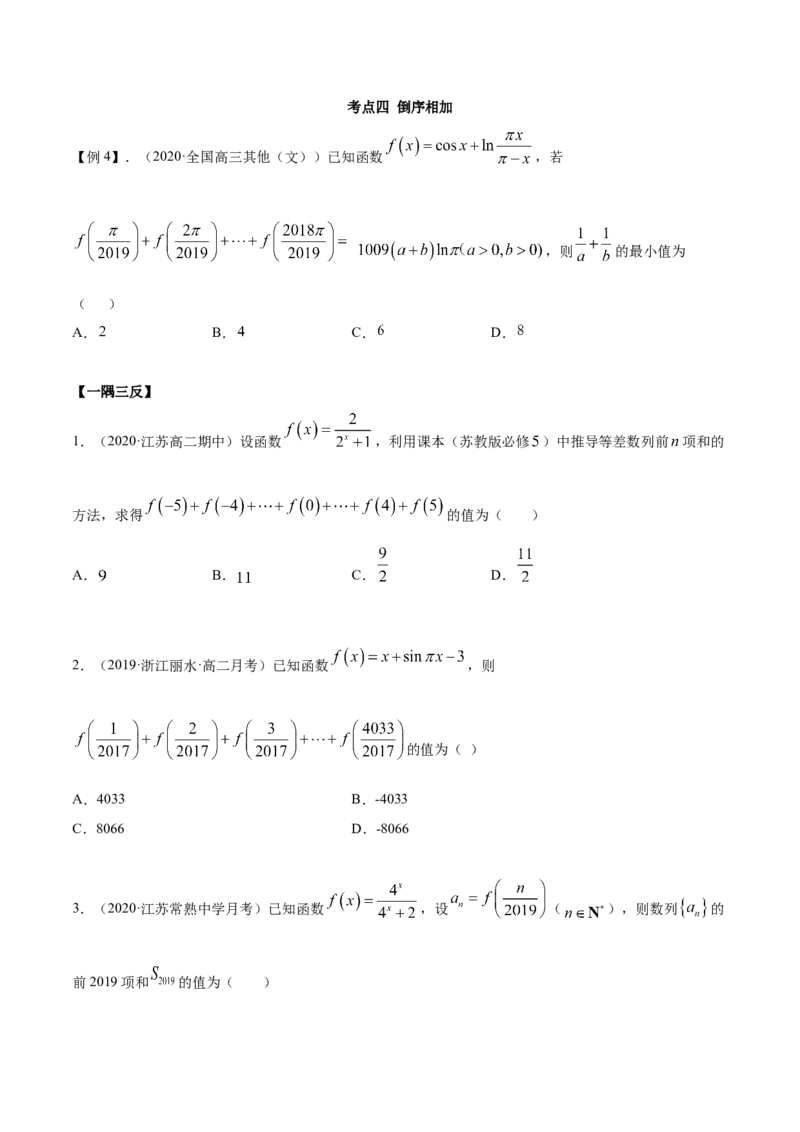文档内容
拓展二 数列求和的方法
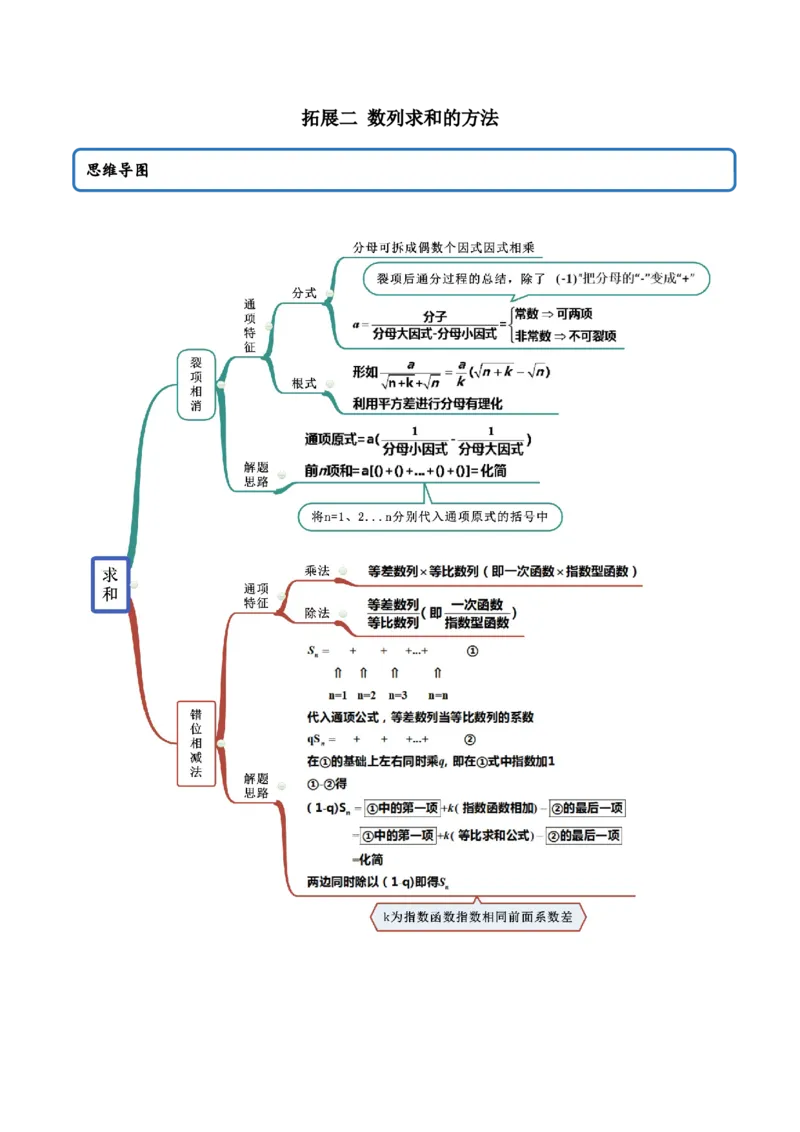
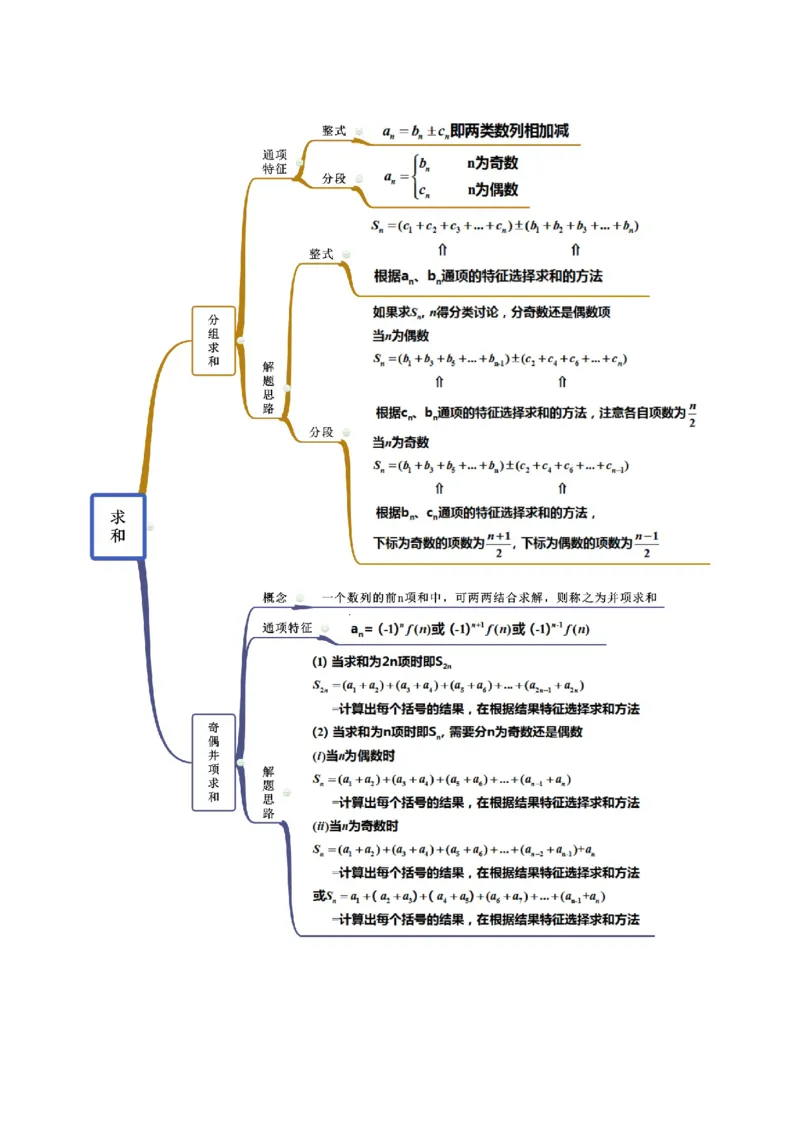
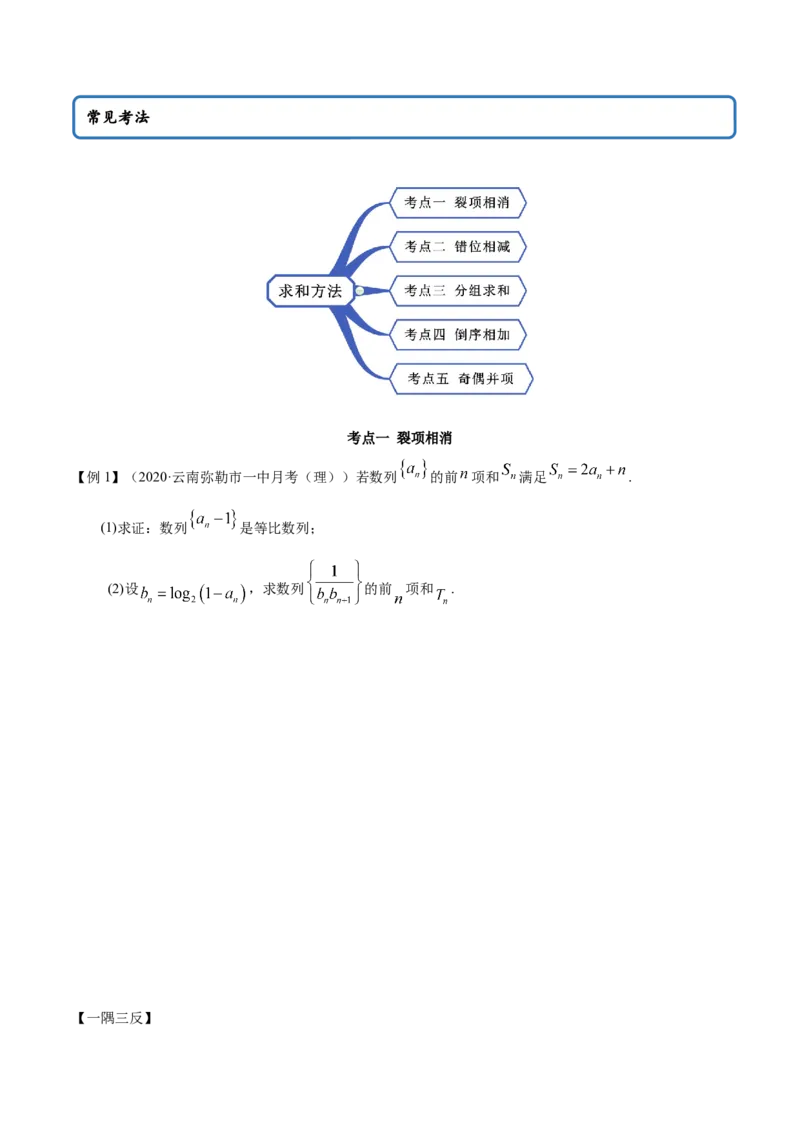
思维导图常见考法
考点一 裂项相消
【例1】(2020·云南弥勒市一中月考(理))若数列 的前 项和 满足 .
(1)求证:数列 是等比数列;
(2)设 ,求数列 的前 项和 .
【一隅三反】1.(2020·湖南天心·长郡中学月考(文))设数列 满足: ,且 ( ),
.
(1)求 的通项公式:
(2)求数列 的前 项和.
2.(2020·石嘴山市第三中学月考)已知 是公差不为零的等差数列, ,且 成等比数列.
(1)求数列 的通项公式;
(2)求数列 的前n项和 .考点二 错位相减
【例2】.(2020·贵州省思南中学月考)已知数列 满足 ,且
(1)求数列 的通项公式;
(2)设 ,求数列 的前 项和 .
【一隅三反】
1.(2020·赣榆智贤中学月考)已知数列 是公差 的等差数列,其前n项和为 ,满足
,且 , , 恰为等比数列 的前三项.
(1)求数列 , 的通项公式;
(2)设 ,数列 的前n项和为 ,求证: .2.(2020·江苏泗阳·桃州中学月考)设数列 、 都有无穷项, 的前 项和为
, 是等比数列, 且 .
(1)求 和 的通项公式;
(2)记 ,求数列 的前 项和为 .
3.(2020·江苏泗阳·桃州中学月考)已知数列 满足 , .
(1)求数列 的通项公式;
(2)求数列 的前 项和 .考点三 分组求和
【例3】.(2020·赣榆智贤中学月考)已知等差数列 的前 项和为 ,等比数列 的前 项和为
.若 , , .
(1)求数列 与 的通项公式;
(2)求数列 的前 项和.
【一隅三反】
1.(2020·河南高二月考)已知数列 的前 项和 ,在各项均不相等的等差数列 中,
,且 , , 成等比数列,
(1)求数列 、 的通项公式;
(2)设 ,求数列 的前 项和 .2.(2020·河南高二月考(理))已知在等比数列 中, ,且 是 和 的等差中项.
(1)求数列 的通项公式;
(2)若数列 满足 ,求 的前 项和 .
3.(2020·天水市第一中学)已知等比数列 的各项均为正数, , .
(1)求数列 的通项公式;
(2)设 ,求数列 的前n项和 .考点四 倒序相加
【例4】.(2020·全国高三其他(文))已知函数 ,若
,则 的最小值为
( )
A. B. C. D.
【一隅三反】
1.(2020·江苏高二期中)设函数 ,利用课本(苏教版必修 )中推导等差数列前 项和的
方法,求得 的值为( )
A. B. C. D.
2.(2019·浙江丽水·高二月考)已知函数 ,则
的值为( )
A.4033 B.-4033
C.8066 D.-8066
3.(2020·江苏常熟中学月考)已知函数 ,设 ( ),则数列 的
前2019项和 的值为( )A. B. C. D.
考点五 奇偶并项
【例5】.(2020·湖南高二月考)设 ,数列 的前 项和为 ,已知 ,
______.请在① , , 成等比数列,② ,③ ,这三个条件中任选一个补充在上面题干中,
并解答下面问题.
(1)求数列 的通项公式;
(2)若数列 满足 ,求数列 的前 项的和 .
【一隅三反】.
1(2019·广东汕头·金山中学高二月考(理))设 是数列 的前n项和,已知 ,
⑴求数列 的通项公式;
⑵设 ,求数列 的前 项和 .2.(2020·内蒙古集宁一中期中(理))已知数列 的前 项和为 .
(1)求数列 的通项公式;
(2)若 ,求数列 的前 项和 .
考点六 绝对值求和
【例6】.(2020·鄂尔多斯市第一中学高二期中(理))已知数列 的通项公式 ,则
( )
A.150 B.162 C.180 D.210【一隅三反】
1.(2020·广东宝安·高二期末)已知 是首项为32的等比数列, 是其前n项和,且 ,则数
列 前10项和为( )
A.58 B.56 C.50 D.45