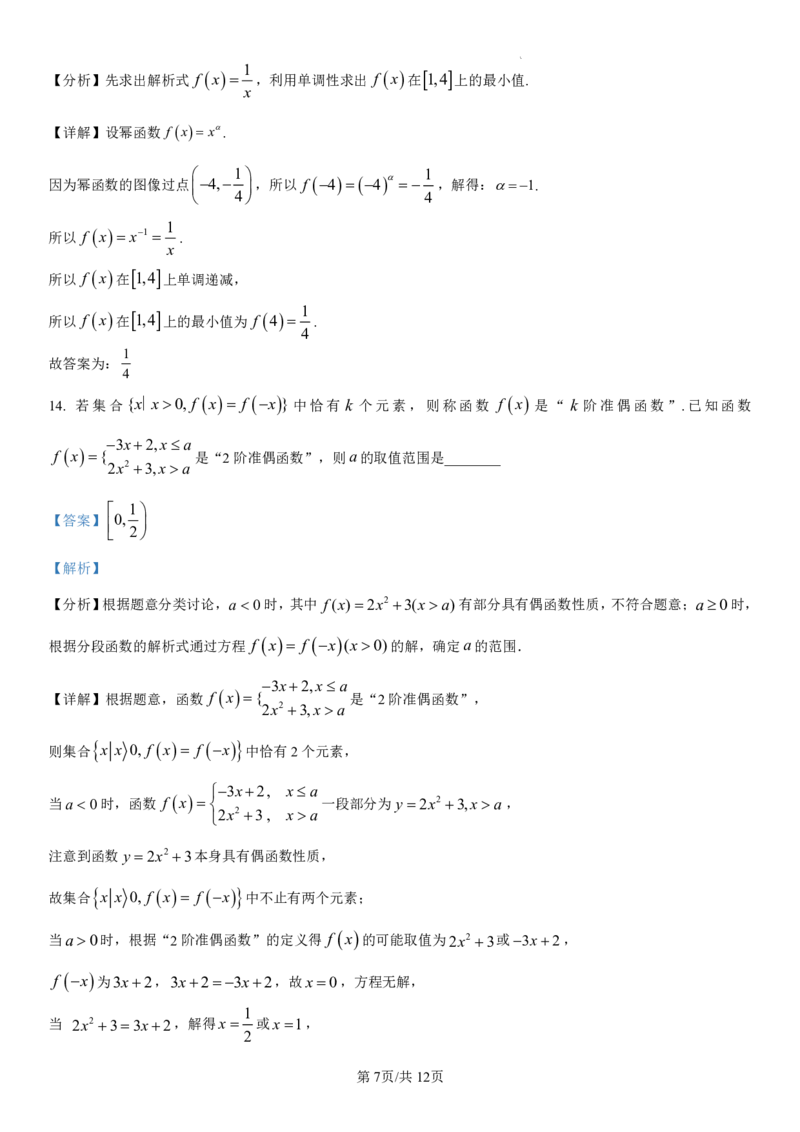吉林省长春第二实验中学2024-2025学年高一上学期期中考试数学PDF版含解析（可编辑）_2024-2025高一（7-7月题库）_2024年12月试卷

长春二实验中学高一上学期期中考试
数学试卷
考生注意：
1．满分 150分，考试时间120分钟．
2．考生作答时，请将答案答在答题卡上．选择题每小题选出答案后，用 2B 铅笔把答题卡上对应题
目的答案标号涂黑；非选择题请用直径 0.5毫米黑色墨水签字笔在答题卡上各题的答题区域内作
答．超出答题区域书写的答案无效，在试题卷、草稿纸上作答无效．
3．本卷命题范围：人教 A版必修第一册第四章 4.4.2结束．
一、选择题：本题共 8小题，每小题5分，共 40分．在每小题给出的四个选项中，只有一项是符合
题目要求的．
1. 命题“
x1,1 
，x2 2x1 ”的否定是（ ）
A.
x1,1，x2
2x1 B.
x1,1，x2
2x 1
C.
x1,1 
，x2 2x 1 D.
x1,1 
，x2 2x1
 5 
2. 已知集合M x 1,xN ，则M 的子集的个数是（ ）

 x 
A.15 B.8 C.7 D.16
1 
3. 若函数 f  3x1  的定义域为 ,1，则函数 f  2x  的定义域为（ ）
3 
1 
A. 0,1 B. ,1 C. 1,1  D.  ,1
3 
4 设a 30.5,blog 6,cln(ln3) ，则（ ）
. 3
A. abc B. bac
C. a cb D. bca
第1页/共4页
学科网（北京）股份有限公司3x
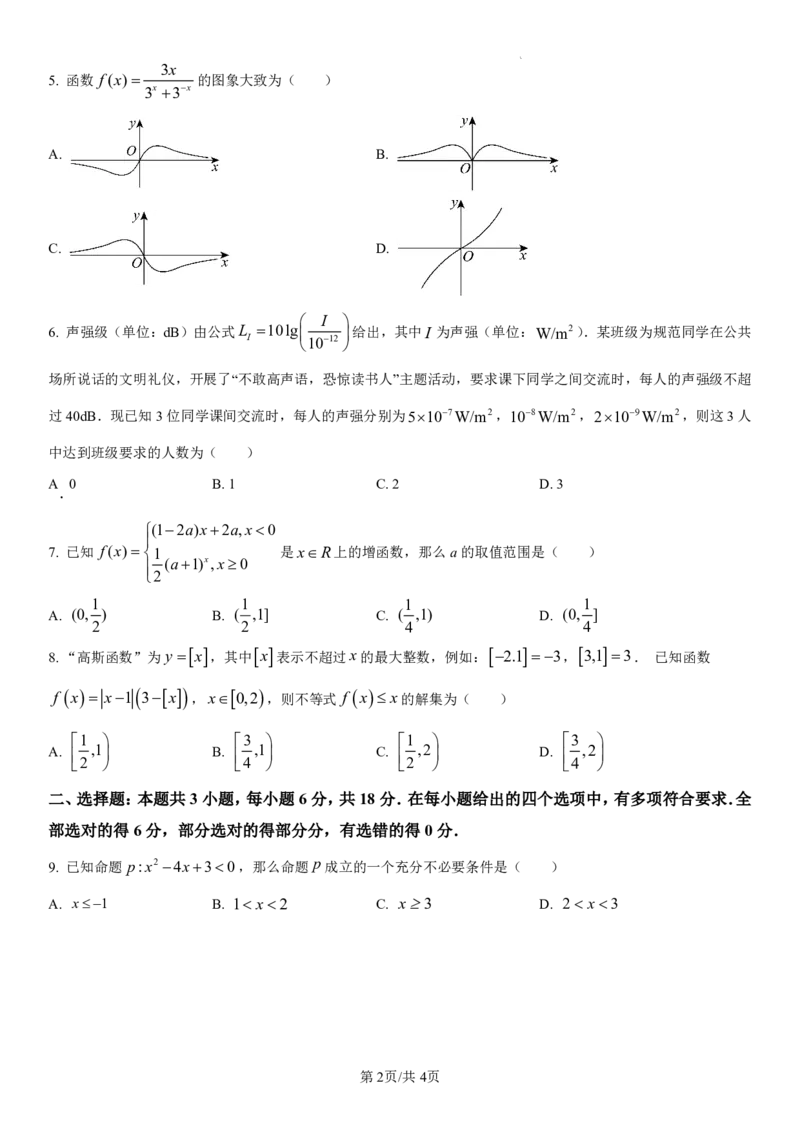
5. 函数 f(x) 的图象大致为（ ）
3x 3x
A. B.
C. D.
 I 
6. 声强级（单位：dB）由公式L 10lg 给出，其中I 为声强（单位：W/m2）．某班级为规范同学在公共
I 1012 
场所说话的文明礼仪，开展了“不敢高声语，恐惊读书人”主题活动，要求课下同学之间交流时，每人的声强级不超
过40dB．现已知3位同学课间交流时，每人的声强分别为5107W/m2，108W/m2，2109W/m2，则这3人
中达到班级要求的人数为（ ）
A 0 B.1 C.2 D.3
.
(12a)x2a,x0

7. 已知 f(x)1 是xR上的增函数，那么a的取值范围是（ ）

(a1)x,x0
2
1 1 1 1
A. (0, ) B. ( ,1] C. ( ,1) D. (0, ]
2 2 4 4
8.“高斯函数”为
y
x

，其中

x

表示不超过x的最大整数，例如：
2.1 3， 
3,1
3．
已知函数
f  x  x1  3 x  ，x 0,2  ，则不等式 f  x  x的解集为（ ）
1  3  1  3 
A.  ,1 B.  ,1 C.  ,2 D.  ,2
2  4  2  4 
二、选择题：本题共 3小题，每小题6分，共18分．在每小题给出的四个选项中，有多项符合要求．全
部选对的得 6分，部分选对的得部分分，有选错的得 0分．
9. 已知命题 p:x2 4x30，那么命题 p成立的一个充分不必要条件是（ ）
A. x1 B. 1 x2 C. x3 D. 2 x3
第2页/共4页
学科网（北京）股份有限公司10. 下列说法正确的有（ ）
1 1
A. 若x ，则2x 的最小值是3
2 2x1
b 1
B. 若a b0，ab1，则 a
2a b
C. 若2ab4，22ab8，则4b2
1 1 1 4
D. 若a0，b0，  1，则  的最小值是4
a b a1 b1
11. 已知函数 f  x log  1x log  3x  （a0且a 1）在定义域内存在最大值，且最大值为2，
a a
g  x  m 2 2 x x 1 ，若对任意x 1     1, 1 2    ，存在x 2 1,1  ，使得 f x 1 gx 2 ，则实数m的取值可以是（ ）
A. 1 B.0 C. log 7 D.3
2
三、填空题：本题共 3小题，每小题 5分，共 15 分．
12. 函数 f  x ax2 1(0a1)的图象恒过定点P，则点P坐标为__________.
 1
13. 若幂函数的图象过点 4, ，则它在  1,4  上的最小值为____．
 4
14. 若集合{x∣x0, f  x  f x  }中恰有 k 个元素，则称函数 f  x  是“ k 阶准偶函数”.已知函数
3x2,xa
f  x { 是“2阶准偶函数”，则a的取值范围是________
2x2 3,xa
四、解答题：本题共 5小题，共 77分．解答应写出文字说明、证明过程或演算步骤．
5 5
15. （1）若3a 5b 15，求  的值；
a b
2
（2）求值： 27  3  lg5 2lg2lg50 3 π  eln1．
1
16. 已知集合A{x|  x2}，B  x∣2m1 xm1  ．
2
1
（1）若m ，求A
ð
B

；
R
2
（2）若“xA”是“xB”的必要条件，求实数m的取值范围．
第3页/共4页
学科网（北京）股份有限公司17. 已知 f  x ln  ex 1  ax是偶函数，g  x ex ex
（1）求a的值；
（2）若不等式g  f  x   g  mx  在  1, 上恒成立，求实数m的取值范围.
18.2024年8月16日，商务部等7部门发布《关于进一步做好汽车以旧换新工作的通知》.根据通知，对符合《汽
车以旧换新补贴实施细则》规定，报废旧车并购买新车的个人消费者，补贴标准由购买新能源乘用车补1万元、购
买燃油乘用车补7000元，分别提高至2万元和1.5万元，某新能源汽车配件公司为扩大生产，计划改进技术生产某
种组件.已知生产该产品的年固定成本为2000万元，每生产x(xN*)百件，需另投入成本W  x  万元，且0 x45
4900
时，W  x 3x2 260x；当x45时，W(x) 501x 4950，由市场调研知，该产品每件的售价为5
x20
万元，且全年内生产的该产品当年能全部销售完.
（1）分别写出0 x  45与x45时，年利润y（万元）与年产量x（百件）的关系式（利润=销售收入-成本）；
（2）当该产品的年产量为多少百件时，公司所获年利润最大？最大年利润是多少？
19. 已知函数 f  x  满足如下条件：①对任意x 0， f  x 0；② f  1 1；③对任意x 0， y 0，总有
f  x  f  y  f  x y  .
（1）写出一个符合上述条件的函数（写出即可，无需证明）；
（2）证明：满足题干条件的函数 f

x

在
 0,
上单调递增；
 
f 2ks
（3）①证明：对任意的s0， 2k ，其中kN*；
 
f s
②证明：对任意的x  2k1,2k kN* ，都有 f  x  f   1   x  2 .
 x 2 x
第4页/共4页
学科网（北京）股份有限公司长春二实验中学高一上学期期中考试
数学试卷
考生注意：
1．满分 150分，考试时间120分钟．
2．考生作答时，请将答案答在答题卡上．选择题每小题选出答案后，用 2B 铅笔把答题卡上对应题
目的答案标号涂黑；非选择题请用直径 0.5毫米黑色墨水签字笔在答题卡上各题的答题区域内作
答．超出答题区域书写的答案无效，在试题卷、草稿纸上作答无效．
3．本卷命题范围：人教 A版必修第一册第四章 4.4.2结束．
一、选择题：本题共 8小题，每小题5分，共 40分．在每小题给出的四个选项中，只有一项是符合
题目要求的．
1. 命题“
x1,1 
，x2 2x1 ”的否定是（ ）
A.
x1,1，x2
2x1 B.
x1,1，x2
2x 1
C.
x1,1 
，x2 2x 1 D.
x1,1 
，x2 2x1
【答案】C
【解析】
【分析】由命题否定的定义即可得解.
【详解】全称量词命题的否定是存在量词命题，故命题“
x1,1 
，x2 2x1”的否定是“
x1,1 
，
x2 2x 1”.
故选：C.
 5 
2. 已知集合M x 1,xN ，则M 的子集的个数是（ ）

 x 
A 15 B.8 C.7 D.16
.
【答案】D
【解析】
【分析】根据不等式的性质，结合子集个数公式进行求解即可.
5
【详解】因为xN ，所以由 15 x x5M  1,2,3,4 ，

x
所以M 的子集的个数是24 16，
故选：D
第1页/共12页
学科网（北京）股份有限公司1 
3. 若函数 f  3x1  的定义域为 ,1，则函数 f  2x  的定义域为（ ）
3 
1 
A. 0,1 B. ,1 C. 1,1  D.  ,1
3 
【答案】A
【解析】
【分析】根据抽象函数的定义域即可得到答案.
【详解】令t 3x1，则t 3x1 0,2 ，
则02x2，解得0 x1，即定义域为0,1 .
故选：A.
4. 设a 30.5,blog 6,cln(ln3) ，则（ ）
3
A. abc B. bac
C. a cb D. bca
【答案】B
【解析】
【分析】根据指数函数与对数函数的单调性质将a，b，c分别与1与3比较即可．
【详解】解：1a 30.5 3，blog
3
6log
3
36log
3
273，
cln(ln3)1，bac．
故选：B．
3x
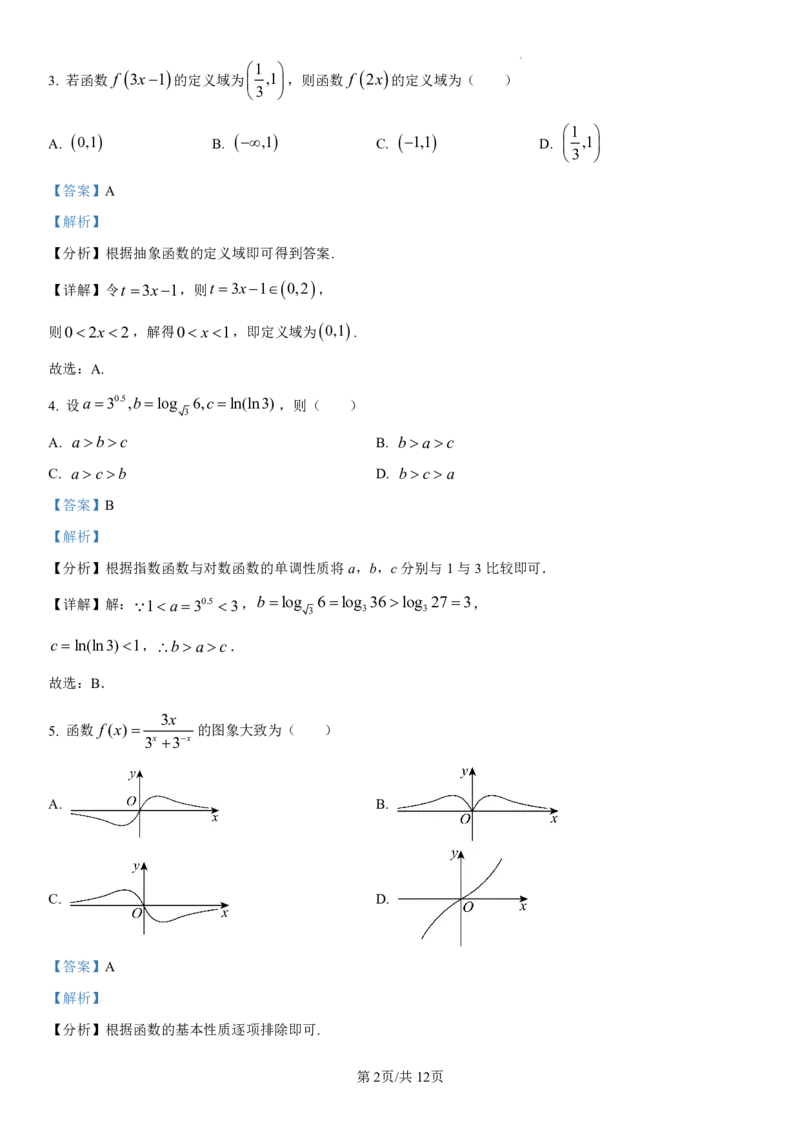
5. 函数 f(x) 的图象大致为（ ）
3x 3x
A. B.
C. D.
【答案】A
【解析】
【分析】根据函数的基本性质逐项排除即可.
第2页/共12页
学科网（北京）股份有限公司3x
【详解】因为 f (x)的定义域为R ，关于原点对称. f(x) f(x)，
3x 3x
所以函数 f (x)是奇函数，即 f (x)的图象关于原点对称，故B错误；
当x 0时，因为3x0，3x 3x 0，
3x
所以 f  x  0，故C错误；
3x 3x
3 9 6 27
因为 f(1)  , f(2)   f(1)，
331 10 932 41
所以 f (x)在(0,)上并不单调递增，故D错误.
故选：A.
 I 
6. 声强级（单位：dB）由公式L 10lg 给出，其中I 为声强（单位：W/m2）．某班级为规范同学在公共
I 1012 
场所说话的文明礼仪，开展了“不敢高声语，恐惊读书人”主题活动，要求课下同学之间交流时，每人的声强级不超
过40dB．现已知3位同学课间交流时，每人的声强分别为5107W/m2，108W/m2，2109W/m2，则这3人
中达到班级要求的人数为（ ）
A.0 B.1 C.2 D.3
【答案】C
【解析】
【分析】根据所给声强级公式计算声强级不超过40dB的声强，即可求解.
 I 
【详解】依题意，L 10lg  40，
I 1012 
∴I 108，
故声强为108W/m2，2109W/m2的两人达到要求，
故选：C
(12a)x2a,x0

7. 已知 f(x)1 是xR上的增函数，那么a的取值范围是（ ）

(a1)x,x0
2
1 1 1 1
A (0, ) B. ( ,1] C. ( ,1) D. (0, ]
.
2 2 4 4
【答案】D
【解析】
【分析】利用函数的单调性，列出不等式组，转化求解a的范围即可．
第3页/共12页
学科网（北京）股份有限公司(12a)x2a,x0

【详解】要使函数 f(x)1 是R上的增函数，
 (a1)x,x 0
2

12a0
 1
需a11 ，解得0a ，
„
 4
1
2a
„
 2
故选：D．
8.“高斯函数”为
y
x

，其中

x

表示不超过x的最大整数，例如：
2.1 3， 
3,1
3．
已知函数
f  x  x1  3 x  ，x 0,2  ，则不等式 f  x  x的解集为（ ）
1  3  1  3 
A.  ,1 B.  ,1 C.  ,2 D.  ,2
2  4  2  4 
【答案】D
【解析】
【分析】先将 f  x  x1  3 x  ，x 0,2  转化为分段函数，然后分类解 f  x  x即可.
【详解】当x 0,1 时，  x 0，x1，此时 f  x 3  1x 33x，
当x 1,2 时，  x 1，x1，此时 f  x 2  x1 2x2，
若 f

x

x，
3 3 
当x 0,1 时， f  x 33x x，得x≥ ，故x

,1，
4 4 
当x 1,2 时， f  x 2x2 x，得x2，故x 1,2 ，
3 
所以 f

x

x得解集为

,2，
4 
故选：D.
二、选择题：本题共 3小题，每小题6分，共18分．在每小题给出的四个选项中，有多项符合要求．全
部选对的得 6分，部分选对的得部分分，有选错的得 0分．
9. 已知命题 p:x2 4x30，那么命题 p成立的一个充分不必要条件是（ ）
A. x1 B. 1 x2 C. x3 D. 2 x3
【答案】BD
【解析】
第4页/共12页
学科网（北京）股份有限公司【分析】解出不等式，再根据充分不必要的条件的判定即可得到答案.
【详解】x2 4x30，解得1 x3，设A x|1 x3 
则命题 p成立的充分不必要条件是集合A的真子集，则BD选项符合题意.
故选：BD.
10. 下列说法正确的有（ ）
1 1
A. 若x ，则2x 的最小值是3
2 2x1
b 1
B. 若a b0，ab1，则 a
2a b
C. 若2ab4，22ab8，则4b2
1 1 1 4
D. 若a0，b0，  1，则  的最小值是4
a b a1 b1
【答案】BCD
【解析】
【分析】根据基本不等式即可求解AD，根据不等式的性质即可求解BC.
1  1  1
【详解】对于A，由题设2x10，则2x   12x  12  12x  11 ，当
 
2x1  12x 12x
且仅当12x1，即x0时等号成立，A错误；
1 b 1 1 b 1
对于B，因为ab1，a b0，所以a 1b0，则a 2a 2，   ，所以 a ，B
b 2a a2a 2 2a b
正确；
对于C，∵22ab8，∴8  b  2a  2，∵2ab4，∴4  2a2b 8，
8b2a2
∵ ，∴12  3b  6 ，∴4b2，故C正确；
42a2b8
1 4 b4a5
对于D，由题设abab，而
a1

b1

ab ab 1
b4a5，
1 1 b 4a b 4a
又b4a  b4a 



  52  59 ，当且仅当b2a3时等号成立，
a b a b a b
1 4
所以  4，D正确．
a1 b1
故选:BCD．
第5页/共12页
学科网（北京）股份有限公司11. 已知函数 f  x log  1x log  3x  （a0且a 1）在定义域内存在最大值，且最大值为2，
a a
g  x  m 2 2 x x 1 ，若对任意x 1     1, 1 2    ，存在x 2 1,1  ，使得 f x 1 gx 2 ，则实数m的取值可以是（ ）
A. 1 B.0 C. log 7 D.3
2
【答案】ABC
【解析】
 1
【分析】先求出 f  x log  x1 2 4  ，得到x 1, 时， f  x  log 72,2  .
2    2   2
再由题意得到log
2
72 m2，即可求出m的范围，对照四个选项即可得到正确答案.
【详解】 f  x  定义域为 3,1  . f  x log  1x log  3x log  x2 2x3  log  x1 2 4 
a a a a  
由题意知x1时， f  x 2，即log 42,a2.
a
此时 f  x log  x1 2 4  ，
2 
 1
x 1, 时， f  x  log 72,2  .
  2   2
1
g  x m
2x
,x1,1 时，g(x)
min
m2，由log
2
72 m2得m
„
log
2
7.
对照四个选项，可以选:ABC.
故答案为：ABC
三、填空题：本题共 3小题，每小题 5分，共 15 分．
12. 函数 f  x ax2 1(0a1)的图象恒过定点P，则点P坐标为__________.
 
【答案】 2,2
【解析】
【分析】根据x20，即可求解x2，代入即可得纵坐标.
【详解】令x20，则x2，故 f  2 a0 12，因此P  2,2  ，
 
故答案为： 2,2
 1
13. 若幂函数的图象过点 4, ，则它在  1,4  上的最小值为____．
 4
1
【答案】 ##0.25
4
【解析】
第6页/共12页
学科网（北京）股份有限公司1
【分析】先求出解析式 f  x  ，利用单调性求出 f  x  在  1,4  上的最小值.
x
【详解】设幂函数 f x x .
 1 1
因为幂函数的图像过点 4, ，所以 f 4 4   ，解得：1.
 4 4
1
所以 f  x  x1  .
x
所以 f  x  在  1,4  上单调递减，
1
所以 f  x  在  1,4  上的最小值为 f  4  .
4
1
故答案为：
4
14. 若集合{x∣x0, f  x  f x  }中恰有 k 个元素，则称函数 f  x  是“ k 阶准偶函数”.已知函数
3x2,xa
f  x { 是“2阶准偶函数”，则a的取值范围是________
2x2 3,xa
 1
【答案】  0, 
 2
【解析】
【分析】根据题意分类讨论，a 0时，其中 f(x)2x2 3(x a)有部分具有偶函数性质，不符合题意；a0时，
根据分段函数的解析式通过方程 f  x  f x  (x0)的解，确定a的范围．
3x2,xa
【详解】根据题意，函数 f

x
{
是“2阶准偶函数”，
2x2 3,xa
则集合

x x 0, f

x

f
x 
中恰有2个元素，
3x2, xa
当a 0时，函数 f  x  一段部分为y 2x2 3,xa，
2x2 3, x a
注意到函数 y 2x2 3本身具有偶函数性质，
故集合

x x 0, f

x

f
x 
中不止有两个元素；
 
当a0时，根据“2阶准偶函数”的定义得 f x 的可能取值为2x2 3或3x2，
f
x 
为3x2，3x23x2，故x0，方程无解，
1
当 2x2 33x2，解得x 或x1，
2
第7页/共12页
学科网（北京）股份有限公司故要使得集合

x x 0, f

x

f
x 
中恰有2个元素，
1 1
则需要满足a ，即0a ，
2 2
3x2,x0
当a 0时，函数 f  x  , f  x  的取值为2x2 3， f x  为3x2，
2x2 3, x0
根据题意得：2x2 33x2，
1
解得x 或x1，满足恰有两个元素，故a 0满足条件.
2
 1
综上，实数a的取值范围是  0, .
 2
 1
故答案为：  0, .
 2
四、解答题：本题共 5小题，共 77分．解答应写出文字说明、证明过程或演算步骤．
5 5
15. （1）若3a 5b 15，求  的值；
a b
2
（2）求值： 27  3  lg5 2lg2lg50 3 π  eln1．
【答案】（1）5；（2）14π
【解析】
【分析】（1）由指对互化求出a和b，再结合换底公式即可求解；
（2）考虑将lg2lg50转化为  1lg5  1lg5  ，进而得解.
1 1 1 1
【详解】（1）因为3a 5b 15，所以a log 15,blog 15，  ,  ，
3 5 a log 15 b log 15
3 5
5 5  1 1 
则  5  5  log 3log 5 5log  35 5；
a b log 15 log 15 15 15 15
3 5
（2） 27  2 3  lg5 2lg2lg50 3 π 1  33 2 3  lg5 2 lg 10 lg  105  π 3 1
5
32  lg5 2 1lg5  1lg5  π 4 13 π  lg5 21  lg5 2  14 π．
1
16. 已知集合A{x|  x2}，B  x∣2m1 xm1  ．
2
1
（1）若m ，求A
ð
B

；
R
2
（2）若“xA”是“xB”的必要条件，求实数m的取值范围．
第8页/共12页
学科网（北京）股份有限公司 3 
【答案】（1）x|  x2
 2 
 3 
（2）m| m 1或m 2
 4 
【解析】
【分析】（1）根据题意，直接由集合的运算，即可得到结果；
（2）根据题意，由条件可得B A，然后分B与B讨论，即可得到结果.
【小问1详解】
1  3
当m 时，B x∣0 x ，
2  2
3
ð B x|x0或x ，
R 2
 3 
则Að B x|  x2.
R  2 
【小问2详解】
因为“xA”是“xB”的必要条件，则B A，
当B时，则m12m1，即m  2；
m12m1

 1 3
当B时，2m1 ，解得 m1，
 2 4
m12

 3 
综上所述，m的取值范围为m| m 1或m 2.
 4 
17. 已知 f  x ln  ex 1  ax是偶函数，g  x ex ex
（1）求a的值；
（2）若不等式g  f  x   g  mx  在  1, 上恒成立，求实数m的取值范围.
1
【答案】（1）a 
2
1
（2）mln  e1 
2
【解析】
【分析】（1）根据函数奇偶性的性质即可求a的值；
（2）根据函数的单调性将不等式g  f  x   g  mx  在  1,＋上恒成立，转化为m f  x x在  1, 上恒
第9页/共12页
学科网（北京）股份有限公司成立，设h

x

f

x
x，求出其最小值，从而得出结果.
【小问1详解】
f

x

的定义域是R ，因为 f

x

是偶函数，所以 f
x 
f

x

恒成立，
所以ln  ex 1  axln  ex 1  ax，
   
即ln ex 1 xaxln ex 1 ax，
所以  2a1  x0恒成立，
1
所以a  ；
2
【小问2详解】
1
g  x ex ex ex  ，xR ，
ex
1 1
因为 y ex是增函数，y  是减函数，所以g  x ex  是增函数，
ex ex
所以不等式g  f  x   g  mx  等价于 f  x mx，
所以m f  x x在  1, 上恒成立，
设h  x  f  x xln  ex 1   1 x，xR ，
2
  1
因为 y ln ex 1 是增函数， y  x是增函数，
2
所以h  x ln  ex 1   1 x是增函数，
2
1
所以当x1时，h  x  h  1 ln  e1  ，
min 2
1
所以mln  e1  .
2
18.2024年8月16日，商务部等7部门发布《关于进一步做好汽车以旧换新工作的通知》.根据通知，对符合《汽
车以旧换新补贴实施细则》规定，报废旧车并购买新车的个人消费者，补贴标准由购买新能源乘用车补1万元、购
买燃油乘用车补7000元，分别提高至2万元和1.5万元，某新能源汽车配件公司为扩大生产，计划改进技术生产某
种组件.已知生产该产品的年固定成本为2000万元，每生产x(xN*)百件，需另投入成本W  x  万元，且0 x45
4900
时，W  x 3x2 260x；当x45时，W(x) 501x 4950，由市场调研知，该产品每件的售价为5
x20
万元，且全年内生产的该产品当年能全部销售完.
（1）分别写出0 x  45与x45时，年利润y（万元）与年产量x（百件）的关系式（利润=销售收入-成本）；
（2）当该产品的年产量为多少百件时，公司所获年利润最大？最大年利润是多少？
【答案】（1）答案见解析；
第10页/共12页
学科网（北京）股份有限公司（2）年产量为50百件时，该企业所获年利润最大，最大年利润是2830万元
【解析】
【分析】（1）结合题意，分0 x  45和x45时利用利润=销售收入-成本求出关系式即可；
（2）当0 x  45时，由二次函数求出最值，当x45时，由基本不等式求出最值，再确定结果即可；
【小问1详解】
由题意可得当0 x  45时， y 500x3x2 260x20003x2 240x2000，
4900 4900
当x45时， y 500x(501x 4950)20002950(x )，
x20 x20
【小问2详解】
由（1）得0 x  45时， y 3x2 240x20003  x40 2 2800，
此时x40（百件）时， y 2800（万元），
max
当x45时，
4900 4900 4900
y2950(x )2970(x20 )29702 (x20) 29702702830，
x20 x20 x20
4900
当且仅当x20 ，即x50时等号成立， y 2800（万元），
x20 max
而28002830，故x50（百件）时，利润最大，
综上所述，年产量为50百件时，该企业所获年利润最大，最大年利润是2830万元.
19. 已知函数 f  x  满足如下条件：①对任意x 0， f  x 0；② f  1 1；③对任意x 0， y 0，总有
f  x  f  y  f  x y  .
（1）写出一个符合上述条件的函数（写出即可，无需证明）；
（2）证明：满足题干条件的函数 f

x

在
 0,
上单调递增；
 
f 2ks
（3）①证明：对任意的s0， 2k ，其中kN*；
 
f s
②证明：对任意的x  2k1,2k kN* ，都有 f  x  f   1   x  2 .
 x 2 x
【答案】（1） f  x  xa a1  （答案不唯一）
（2）证明见解析 （3）①证明见解析；②证明见解析
【解析】
【分析】（1）根据条件设计一个函数即可；
（2）根据条件，运用函数单调性的定义推导即可；
第11页/共12页
学科网（北京）股份有限公司（3）运用递推的方法先证明①，再根据①的结论，考虑的x的区间即可证明.
【小问1详解】
f  x  x， f  x  x2， f  x  x3等，即形如 f  x  x1  均可；
【小问2详解】
任取x  y 0， f  x  f  y  f  x y y  f  y  .
因为x y0，故 f  x y y  f  x y  f  y  且 f  x y 0.
故 f  x  f  y  f  x y y  f  y  f  x y 0.
故 f

x

在
 0,
上单调递增.
【小问3详解】
①由题意可知：对任意正数s，都有 f  s 0，且 f  s  f  t  f  st  ，
 
f 2s
在③中令x y s，可得 f  2s 2f  s  ，即 2；
 
f s
f  2ks  f  2ks  f  2k1s  f  2s 
故对任意正整数k与正数s，都有     2k；
f  s  f  2k1s  f  2k2s  f  s 
②由①可知：对任意正整数k与正数s，都有 f  2ks  2k f  s  ，
故对任意正整数k与正数s，都有 f  2k1s  2k1 f  s  ，
令s21k，则 f  21k  21k f  1 21k ；
对任意x  2k1,2k  kN*  ，可得 1   2k,21k  ，并且2k2  x 2k1, 21k  2 22k ，
x 2 x
又因为 f

1
1，所以由（2）中已经证明的单调性可知：
f  x  f  2k1  2k1f  1 2k1  x ， f   1   f  21k  21k  2 ，
2  x x
1 x 2
所以 f  x  f     .
 x 2 x
【点睛】对于第二问，如何巧妙运用 f  x  f  y  f  x y  要学习，抽象函数中经常会用到这个方法；对于第
三问，可以把2ks 看作 s    s    s      s ，再运用 f  x  f  y  f  x y  可以证明①，再利用①的结论推出
2k
x 1 2
f  x  ， f    .
2  x x
第12页/共12页
学科网（北京）股份有限公司