文档内容
3.2.1双曲线及其标准方程 -B提高练
一、选择题
x2
1.(2020·山东菏泽三中高二期末)与椭圆 +y2=1共焦点且过点P(2,1)的双曲线方程是( )
4
x2 x2 x2 y2
A. -y2=1 B. -y2=1 C. -y2=1 D.x2- =1
4 3 2 2
2.动圆与圆x2+y2=1和x2+y2-8x+12=0都外切,则动圆圆心的轨迹是( )
A.双曲线的一支 B.圆 C.椭圆 D.双曲线
y2
3.设F,F 分别是双曲线x2- =1的左、右焦点.若P在双曲线上,且⃗PF ·⃗PF =0,则|⃗PF +⃗PF |=
1 2 9 1 2 1 2
( )
A.2√5 B.√5 C.2√10 D.√10
4.(2020·武汉市蔡甸区实验高级中学月考)已知双曲线 和椭圆
有相同的焦点,则 的最小值为( )
A.2 B.3 C.4 D.5
5.(多选题)(2020·江苏省镇江中学高二期末)在平面直角坐标系 中,动点P到两个定点
和 的斜率之积等于8,记点P的轨迹为曲线E,则( )
A.曲线E经过坐标原点 B.曲线E关于x轴对称
C.曲线E关于y轴对称 D.若点 在曲线E上,则
6. (多选题)(2020·广东宝安高二开学考试)已知点 在双曲线 上, 、 是双
曲线 的左、右焦点,若 的面积为 ,则下列说法正确的有( )
A.点 到 轴的距离为 B.C. 为钝角三角形 D.
二、填空题
y2
7.已知F是双曲线C:x2- =1的右焦点,P是C上一点,且PF与x轴垂直,点A的坐标是(1,3),则△APF
3
的面积为 .
8.(2020·首都师范大学附属中学期中)若方程 所表示的曲线为 ,给出下列四个
命题:①若 为椭圆,则实数 的取值范围为 ;
②若 为双曲线,则实数 的取值范围为 ;
③曲线 不可能是圆;
④若 表示椭圆,且长轴在 轴上,则实数 的取值范围为 .
其中真命题的序号为________.(把所有正确命题的序号都填在横线上)
9.(2020·全国高二课时练习)已知圆 与y轴的两个交点A,B都在某双曲线上,
且A,B两点恰好将此双曲线的焦距三等分,则此双曲线的标准方程为________.
10.平面上两点F,F 满足|F F|=4,设d为实数,令D表示平面上满足||PF |-|PF ||=d的所有P点组成的
1 2 1 2 1 2
图形,又令C为平面上以F 为圆心、6为半径的圆.下列结论中,其中正确的有 (写出所有正
1
确结论的编号).
①当d=0时,D为直线; ②当d=1时,D为双曲线;
③当d=2时,D与圆C交于两点; ④当d=4时,D与圆C交于四点;
⑤当d>4时,D不存在.
三、解答题
3
11.在周长为48的Rt MPN中,∠MPN=90°,tan∠PMN= ,求以M,N为焦点,且过点P的双曲线方程.
4
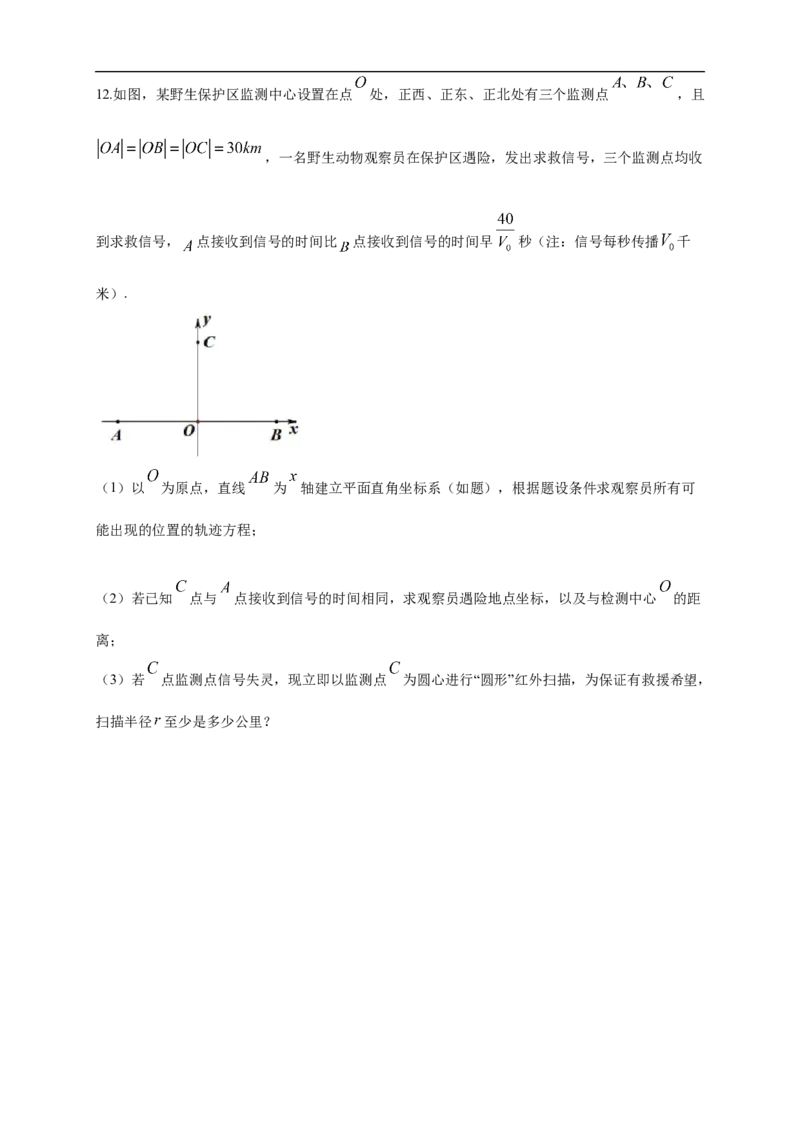
△12.如图,某野生保护区监测中心设置在点 处,正西、正东、正北处有三个监测点 ,且
,一名野生动物观察员在保护区遇险,发出求救信号,三个监测点均收
到求救信号, 点接收到信号的时间比 点接收到信号的时间早 秒(注:信号每秒传播 千
米).
(1)以 为原点,直线 为 轴建立平面直角坐标系(如题),根据题设条件求观察员所有可
能出现的位置的轨迹方程;
(2)若已知 点与 点接收到信号的时间相同,求观察员遇险地点坐标,以及与检测中心 的距
离;
(3)若 点监测点信号失灵,现立即以监测点 为圆心进行“圆形”红外扫描,为保证有救援希望,
扫描半径 至少是多少公里?