文档内容
3.2.1双曲线及其标准方程 -A基础练
一、选择题
1.(2020·全国高二课时练习)已知点 的坐标满足 ,
则动点P的轨迹是( )
A.椭圆 B.双曲线 C.两条射线 D.双曲线的一支
【答案】B
【解析】设 ,则由已知得 即动点P到两个定点A、B的距离之差
的绝对值等于常数 ,又 ,且 ,所以根据双曲线的定义知,动点P的轨迹是双曲
线.故选:B
2.(2020·广东云浮·高二期末)已知双曲线 的左、右焦点分别为 ,点P是该双曲
线上的一点,且 ,则 ( )
A.2或18 B.2 C.18 D.4
【答案】C
【解析】在双曲线 中, , , ,因为 ,
所以点P在该双曲线左支上,则 ,故选:C.
3.(2020·全国高二课时练习)已知F是双曲线C: 的右焦点,P是C上一点,且PF
与x轴垂直,点A的坐标是(1,3),则 的面积为
A. B. C. D.
【答案】D
【解析】由 得 ,所以 ,将 代入 ,得 ,所以,又点A的坐标是(1,3),故△APF的面积为 ,选D.
4.(2020·梅河口市第五中学高二月考)数学家华罗庚曾说:“数缺形时少直观,形少数时难入
微”事
实上,很多代数问题可以转化为几何问题加以解决,例如,与 相关的代数问
题,可以转化为点 与点 之间的距离的几何问题.结合上述观点,可得方程
的解为( )
A. B. C. D.
【答案】C
【解析】由 ,得 ,
其几何意义为平面内动点 与两定点 , 距离差的绝对值为4.
平面内动点与两定点 , 距离差的绝对值为4的点的轨迹是双曲线,
由题得 ,解之得 .
所以平面内动点与两定点 , 距离差的绝对值为4的点的轨迹方程是
.联立 ,解得 .故选:C.
5.(多选题)(2020·无锡市第一中学期中)已知 两监测点间距离为800米,且 监测点听到
爆炸声的时间比 监测点迟2秒,设声速为340米/秒,下列说法正确的是( )
A.爆炸点在以 为焦点的椭圆上B.爆炸点在以 为焦点的双曲线的一支上
C.若 监测点的声强是 监测点的4倍(声强与距离的平方成反比),则爆炸点到 监测点的距离
为 米
D.若 监测点的声强是 监测点的4倍(声强与距离的平方成反比),则爆炸点到 监测点的距离
为 米
【答案】BD
【解析】依题意, 两监测点间距离为800米,且 监测点听到爆炸声的时间比 监测点迟2
秒,
设爆炸点为 ,则 ,所以爆炸点在以 为焦点的双曲线的一
支上.所以A选项错误,B选项正确.若 监测点的声强是 监测点的4倍(声强与距离的平方成反
比),所以 ,即 ,结合 可得 .
所以C选项错误,D选项正确.故选:BD
6.(多选题)若方程 所表示的曲线为 ,则下面四个命题中错误的是( )
A.若 为椭圆,则 B.若 为双曲线,则 或
C.曲线 可能是圆 D.若 为椭圆,且长轴在 轴上,则
【答案】AD
【解析】若 ,则方程可变形为 ,它表示焦点在 轴上的双曲线;若 ,则方程可变形为 ,它表示焦点在 轴上的双曲线;
若 ,则 ,故方程 表示焦点在 轴上的椭圆;
若 ,则 ,故方程 表示焦点在 轴上的椭圆;
若 ,方程 即为 ,它表示圆,综上,选AD.
二、填空 题
7. (2020·全国高二课时练)已知双曲线 的一个焦点是 ,椭圆
的焦距等于 ,则 ________.
【答案】5
【解析】因为双曲线的焦点是 ,所以双曲线的标准方程是 ,即
, ,即 ,所以椭圆方程是 ,因为焦距
,所以 ,即 ,解得 .
8.若双曲线 的一个焦点到坐标原点的距离为3,则m的值为______.
【答案】7或
【解析】依题意可知 ,当双曲线的焦点在x轴上时, ,所以 ;
当双曲线的焦点在y轴上时, ,所以 综上, 或 .
x2
9. (2020·全国高二课时练)若双曲线 -y2=1(n>1)的左、右焦点分别为F,F,点P在双曲线上,且满
1 2
n
足|PF |+|PF |=2√n+2,则△PFF 的面积为______.
1 2 1 2【答案】1
【解析】设点P在双曲线的右支上,则|PF |-|PF |=2√n,已知|PF |+|PF |=2√n+2,
1 2 1 2
解得|PF |=√n+2+√n,|PF |=√n+2-√n,|PF |·|PF |=2.又|F F|=2√n+1,
1 2 1 2 1 2
1 1
则|PF |2+|PF |2=|F F|2,∴△PFF 为直角三角形,∠FPF=90°,∴S = |PF |·|PF |= ×2=1.
1 2 1 2 1 2 1 2 △PF 1 F 2 2 1 2 2
10.焦点在x轴上的双曲线经过点P(4√2,-3),且Q(0,5)与两焦点的连线互相垂直,则此双曲线的标准方
程为 .
x2 y2
【答案】 - =1.
16 9
5 5
【解析】设焦点F(-c,0),F(c,0)(c>0),则由QF⊥QF,得k ·k =-1,∴ · =-1,∴c=5.
1 2 1 2 QF 1 QF 2 c -c
设 双 曲 线 方 程 为 x2 y2 =1(a>0,b>0),∵ 双 曲 线 过 点 (4 ,-3),∴ 32 9 =1, 又
- √2 -
a2 b2 a2 b2
x2 y2
∵c2=a2+b2=25,∴a2=16,b2=9,∴双曲线的标准方程为 - =1.
16 9
三、解答题
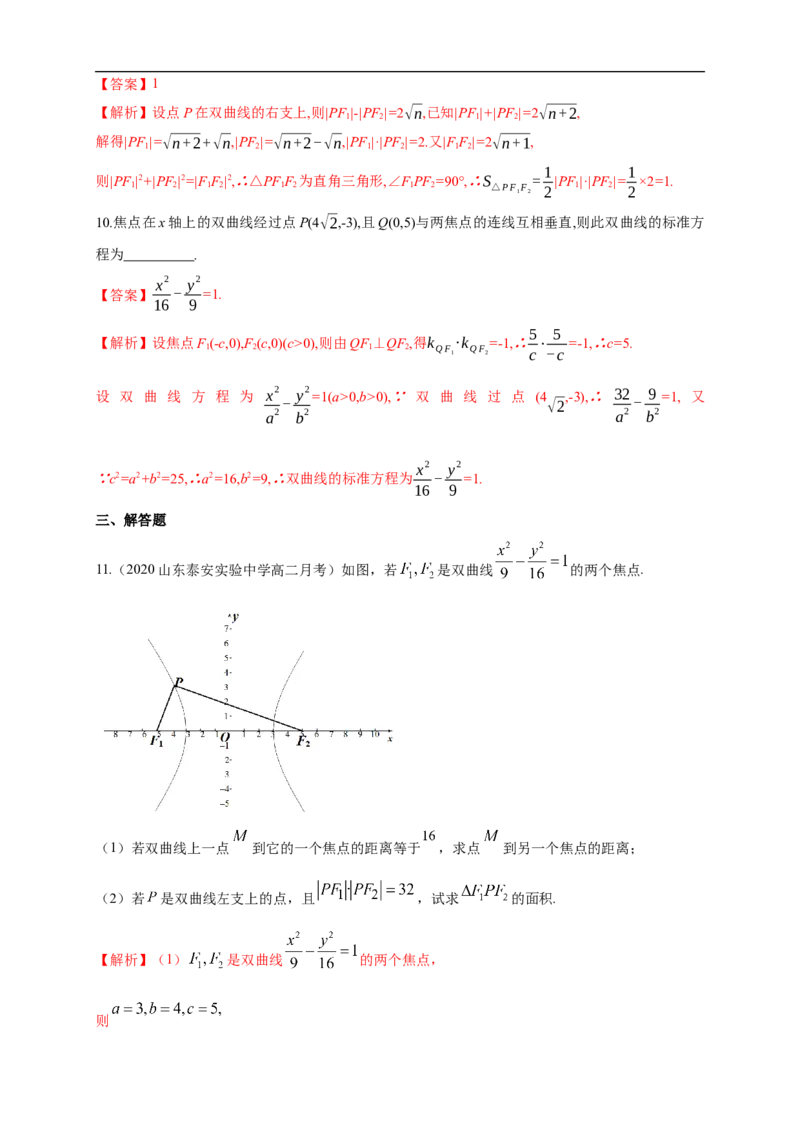
11.(2020山东泰安实验中学高二月考)如图,若 是双曲线 的两个焦点.
(1)若双曲线上一点 到它的一个焦点的距离等于 ,求点 到另一个焦点的距离;
(2)若 是双曲线左支上的点,且 ,试求 的面积.
【解析】(1) 是双曲线 的两个焦点,
则设点 到另一个焦点的距离为 ,
由抛物线定义可知 ,解得 或 ,
即点 到另一个焦点的距离为 或 .
(2) 是双曲线左支上的点, ,
则 ,
代入 ,
可得 ,
即 ,
所以 为直角三角形,
所以 .
12.如图所示,已知定圆F:(x+5)2+y2=1,定圆F:(x-5)2+y2=42,动圆M与定圆F,F 都外切,求动圆圆心M
1 2 1 2
的轨迹方程.
【解析】圆F:(x+5)2+y2=1,圆心F(-5,0),半径r=1;
1 1 1
圆F:(x-5)2+y2=42,圆心F(5,0),半径r=4.
2 2 2
设动圆M的半径为R,则有|MF |=R+1,|MF |=R+4,
1 2
∴|MF |-|MF |=3<10=|F F|.
2 1 1 2
3 91
∴点M的轨迹是以F,F 为焦点的双曲线的左支,且a= ,c=5,于是b2=c2-a2= .
1 2
2 4
x2 y2
- ( 3)
∴动圆圆心M的轨迹方程为 9 91=1 x≤- .
2
4 4