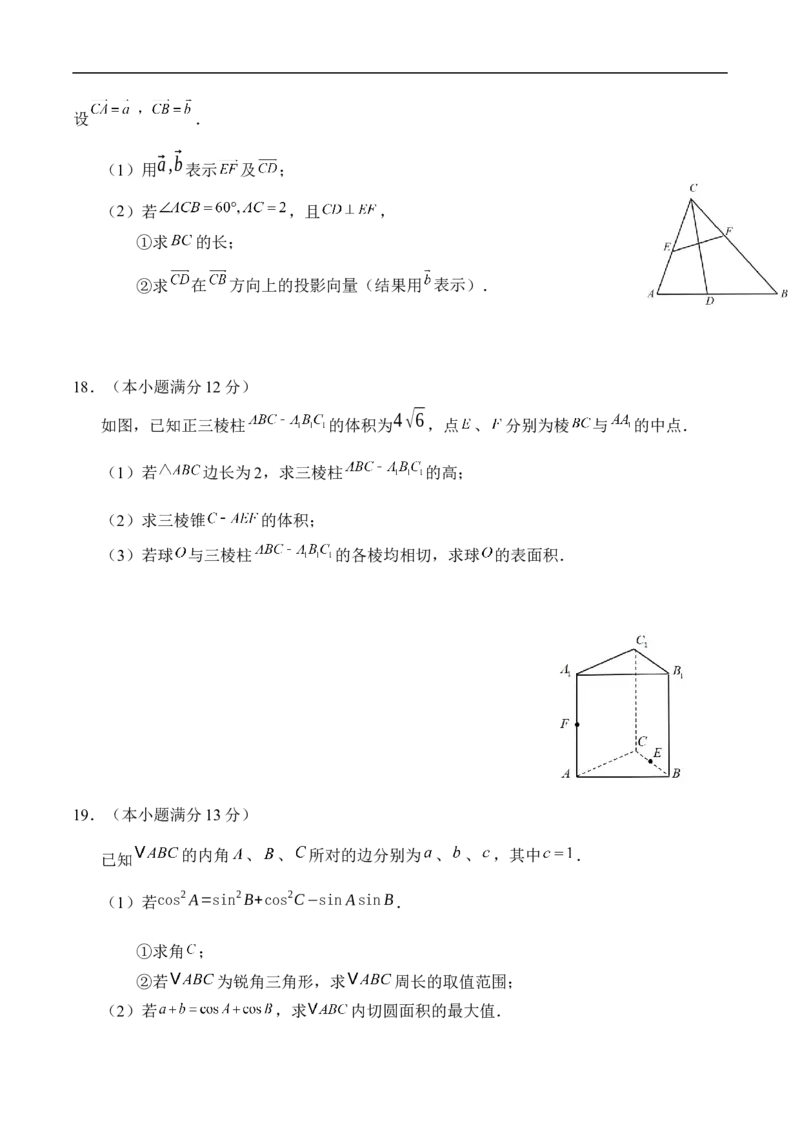
文档内容
2024~2025 学年度第二学期期中重点校联考高一数学
第Ⅰ卷(共36分)
一、选择题(本题共9小题,每题4分,共36分)
1. 为虚数单位,若 ,则
A.1 B. C.2 D.
2.在ΔABC 中, a,b 是角 A,B 的对边, a=2,b=√6,A=45° ,则角B的值为
A.
60°
B.
150°
C.
30°或 150°
D.
60°或 120°
3.设 x,y∈R ,向量 ⃗a=(x,1) , ⃗b=(1,y) , ⃗c=(2,−4) ,且 ⃗a⊥⃗c , ⃗b//⃗c ,则x+y=
A.0 B.1 C.2 D.3
4.一个四边形用斜二测画法得到的直观图是一个底角为
45°,腰和上底长均为1的等腰梯形
则该四边形原来的面积为
√2+2
A.
2+√2
B.
8
3√2 √2+1
2 2
C. D.
5.若球的表面积扩大到原来的9倍,那么该球的体积扩大到原来的( )倍
A.9 B.27 C.81 D.7296.已知甲船位于灯塔A的北偏东 70°方向,且与A相距3海里,乙船位于灯塔A的北偏西
50°方向,若两船相距
√19
海里,则乙船与灯塔A之间的距离为
2√3
A. B.2 C. D.5
7.若某圆锥的侧面展开图是一个半径为 2的半圆面,其内接正四棱柱的高为 ,则此正
四棱柱的体积是
A. B. C. D.
8.四边形 ABCD 是边长为1的正方形,延长 CD 至E,使得 C⃗D= ⃗DE ,若点F为线段AE上
的动点,则 的最小值为
A. B.1 C. D.2
ΔABC a,b,c A,B,C
9.在 中, 分别是角 的对边,下列四个命题中正确的个数为
①若bcosC+ccosB=b,则ΔABC
是等腰三角形;
②若acosA=bcosB,则ΔABC是等腰三角形;
③若a2 +b2 −c2 >0,则ΔABC
一定是锐角三角形;
④在ΔABC 中,A=60°, a=√6 ,若ΔABC 有一个解,则b的取值范围是 b=2√2 或0− 且λ≠2
2
12.
13.
. ,
14
三、解答题(本题共5小题,共59分)
15.(本小题满分10分)
{m≠−1且m≠2¿¿¿¿
(1)若z是纯虚数,则
解得 . ………………………5分
{m<−1或m>2¿¿¿¿
2)
(
解得 . ………………………10分
16.(本小题满分12分)
(1)因为 ,由正弦定理可得 , ………………………2分
整理得 ,
由余弦定理可得 ,
且 ,所以 . …………………5分
(2)由正弦定理知 ,∴ ,∴ …………6分
又 ,∴ ,∴ , ……………………7分
……………………9分
∴ . ……………………10分
∴
……………………12分
17.(本小题满分12分)
(1)因为 ,
所以, ; ………………………2分
……4分
(2)①因为 ,所以 , …………6分
所以 ,由 ,可得 ,即BC=3 ………………8分② 方向上的投影向量为
………………10分
…………………12分
18.(本小题满分12分)
(1)设 的高为
1
S = ×√3×2=√3
△ABC 2 …………………2分
V
ABC−A B C 4√6
h= 1 1 1= =4√2
S △ABC √3 …………………4分
V =V
(2)
C−AEF F−ACE
1
= ⋅S ⋅AF
3 △ACE
1 1 1
= ⋅ S ⋅ AA
3 2 △ABC 2 1
…………………6分
1
= V
12 ABC−A B C
1 1 1
1
= ×4√6
12
√6
=
3
…………………8分
(3)设正三棱柱 的底面边长为 ,高为 ,上底面中心为 ,下底面中心为 ,
连接 ,则球 的球心 在 的中点上
球 切棱 于 ,切棱 于
由题意 ,①
因为 , ,又 ,所以 ,
所以 ,解得 ② …………………10分
联立①②可得 ,所以球 的半径为 ,
所以球 的表面积为 …………12分
19.(本小题满分13分)
(1)①cos2A=sin2B+cos2C−sinAsinB
⇒1−sin2A=sin2B+1−sin2C−sinAsinB
1
⇒b2 +a2 −c2 =ab⇒cosC=
2 ………………2分
π
∵0