文档内容
静海⼀中 第⼀学期⾼⼀数学( ⽉)
2025-2026 12
学⽣学业能⼒调研试卷
命题⼈ 邹鑫鹏 审题⼈ 陈中友
考⽣注意:
本试卷分第Ⅰ卷基础题(99分)和第Ⅱ卷提⾼题(18分)两部分共 117分,3分卷⾯分,满
分共120分.
第Ⅰ卷 基础题(共99分)
⼀、选择题:(每⼩题4分,共28分).
1. 设集合 , ,则集合 ( )
A B. C. D.
2. 已知命题 ,那么 ( )
A. B.
C. D.
3. 函数 的零点所在区间是( )
A. B. C. D.
4. 下列命题为真命题的是( )
A. 若 ,则 B. 若 ,则
C. 若 ,则 D. 若 ,则
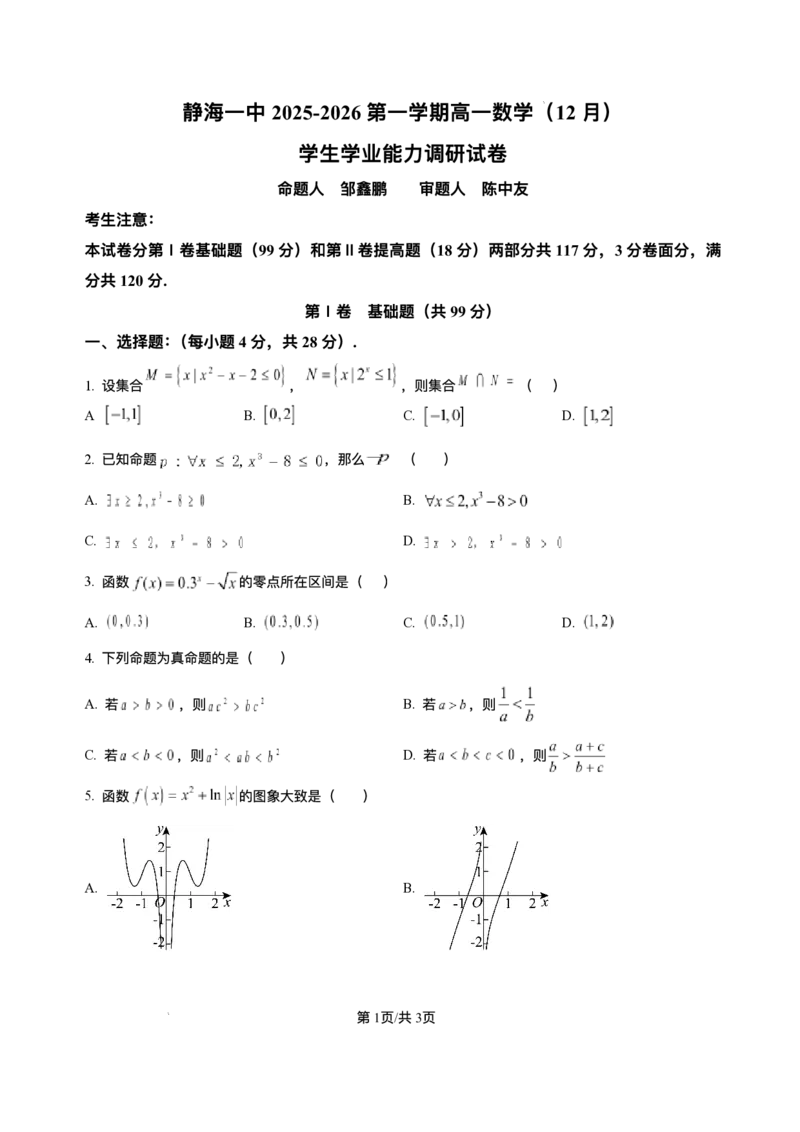
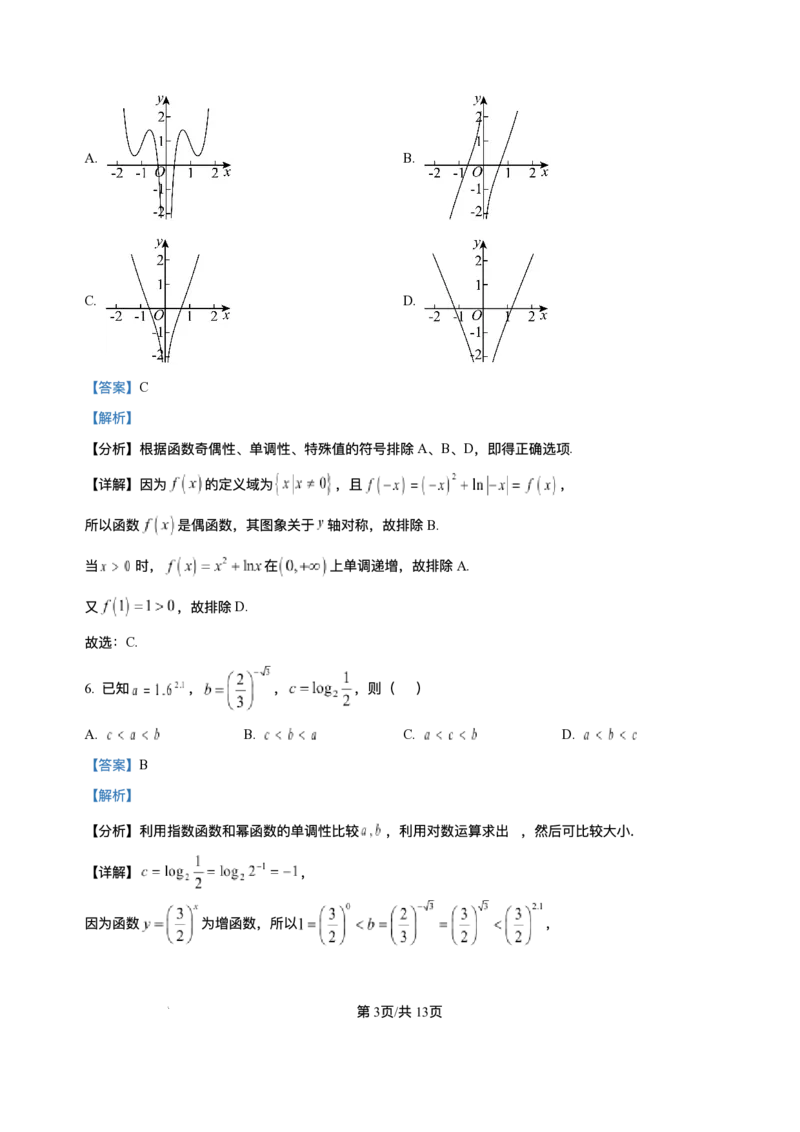
5. 函数 的图象⼤致是( )
A. B.
第1⻚/共3⻚
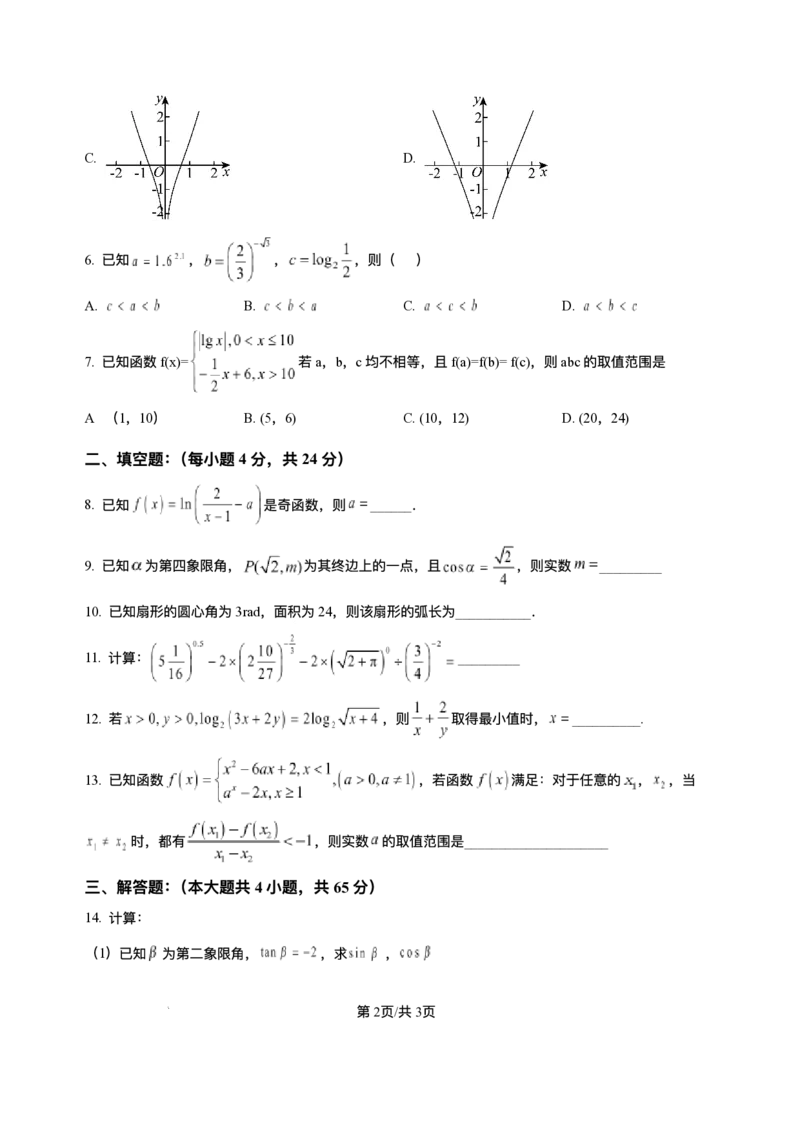
学科⽹(北京)股份有限公司C. D.
6. 已知 , , ,则( )
A. B. C. D.
7. 已知函数f(x)= 若a,b,c均不相等,且f(a)=f(b)=f(c),则abc的取值范围是
A (1,10) B.(5,6) C.(10,12) D.(20,24)
⼆、填空题:(每⼩题4分,共24分)
8. 已知 是奇函数,则 ______.
9. 已知 为第四象限⻆, 为其终边上的⼀点,且 ,则实数 _________
10. 已知扇形的圆⼼⻆为3rad,⾯积为24,则该扇形的弧⻓为___________.
11. 计算: _________
12. 若 ,则 取得最⼩值时, __________.
13. 已知函数 ,若函数 满⾜:对于任意的 , ,当
时,都有 ,则实数 的取值范围是_____________________
三、解答题:(本⼤题共4⼩题,共65分)
14. 计算:
(1)已知 为第⼆象限⻆, ,求 ,
第2⻚/共3⻚
学科⽹(北京)股份有限公司(2)已知 ,
(ⅰ)求 的值;
(ⅱ)求 的值.
15. 已知函数 ,其中 且 .
(1)求 的值和函数 的定义域;
(2)判断并证明函数 奇偶性;
(3)求不等式 的解集.
16
(1)若不等式 对于 恒成⽴,求实数k的取值范围;
(2)若函数 ( , )在区间 上单调递减,求实数a的取值范围;
(3)已知不等式 对满⾜ 的⼀切实数 恒成⽴求 的取值范围;
(4)你认为解决恒成⽴问题的本质是什么?
第Ⅱ卷 提⾼题(共18分)
17. 已知 .
(1)求证: ;
(2)判断 的单调性,并⽤单调性的定义证明;
(3)当 时, 恒成⽴,求实数 的取值范围.
第3⻚/共3⻚
学科⽹(北京)股份有限公司静海⼀中 第⼀学期⾼⼀数学( ⽉)
2025-2026 12
学⽣学业能⼒调研试卷
命题⼈ 邹鑫鹏 审题⼈ 陈中友
考⽣注意:
本试卷分第Ⅰ卷基础题(99分)和第Ⅱ卷提⾼题(18分)两部分共 117分,3分卷⾯分,满
分共120分.
第Ⅰ卷 基础题(共99分)
⼀、选择题:(每⼩题4分,共28分).
1. 设集合 , ,则集合 ( )
A. B. C. D.
【答案】C
【解析】
【分析】解不等式将集合具体化,然后由交集定义可得.
【详解】解不等式 得 ,所以 ,
解不等式 得 ,所以 ,
所以 .
故选:C
2. 已知命题 ,那么 是( )
A. B.
C. D.
【答案】C
【解析】
【分析】根据全称命题的否定为特称命题解答即可;
【详解】解:命题 为全称命题,其否定为 ,
故选:C
3. 函数 的零点所在区间是( )
第1⻚/共13⻚
学科⽹(北京)股份有限公司A. B. C. D.
【答案】B
【解析】
【分析】利⽤指数函数与幂函数的单调性结合零点存在性定理计算即可.
【详解】由指数函数、幂函数的单调性可知: 在 上单调递减, 在 单调递增,
所以 在定义域上单调递减,
显然 ,
所以根据零点存在性定理可知 的零点位于 .
故选:B
4. 下列命题为真命题的是( )
A. 若 ,则 B. 若 ,则
C. 若 ,则 D. 若 ,则
【答案】D
【解析】
【分析】根据反例可判断ABC的正误,根据不等式的性质可判断D的正误.
【详解】对于A:当 时, ,因此A不是真命题;
对于B:取 , ,但是 ,因此B不是真命题,
对于C:取 , ,此时 ,但 ,因此C不是真命题;
对于D:若 ,则 恒成⽴,即 ,
因此D正确
故选:D.
5. 函数 的图象⼤致是( )
第2⻚/共13⻚
学科⽹(北京)股份有限公司A. B.
C. D.
【答案】C
【解析】
【分析】根据函数奇偶性、单调性、特殊值的符号排除A、B、D,即得正确选项.
【详解】因为 的定义域为 ,且 ,
所以函数 是偶函数,其图象关于 轴对称,故排除B.
当 时, 在 上单调递增,故排除A.
⼜ ,故排除D.
故选:C.
6. 已知 , , ,则( )
A. B. C. D.
【答案】B
【解析】
【分析】利⽤指数函数和幂函数的单调性⽐较 ,利⽤对数运算求出 ,然后可⽐较⼤⼩.
【详解】 ,
因为函数 为增函数,所以 ,
第3⻚/共13⻚
学科⽹(北京)股份有限公司⼜函数 在 上单调递增,所以 ,所以 .
故选:B
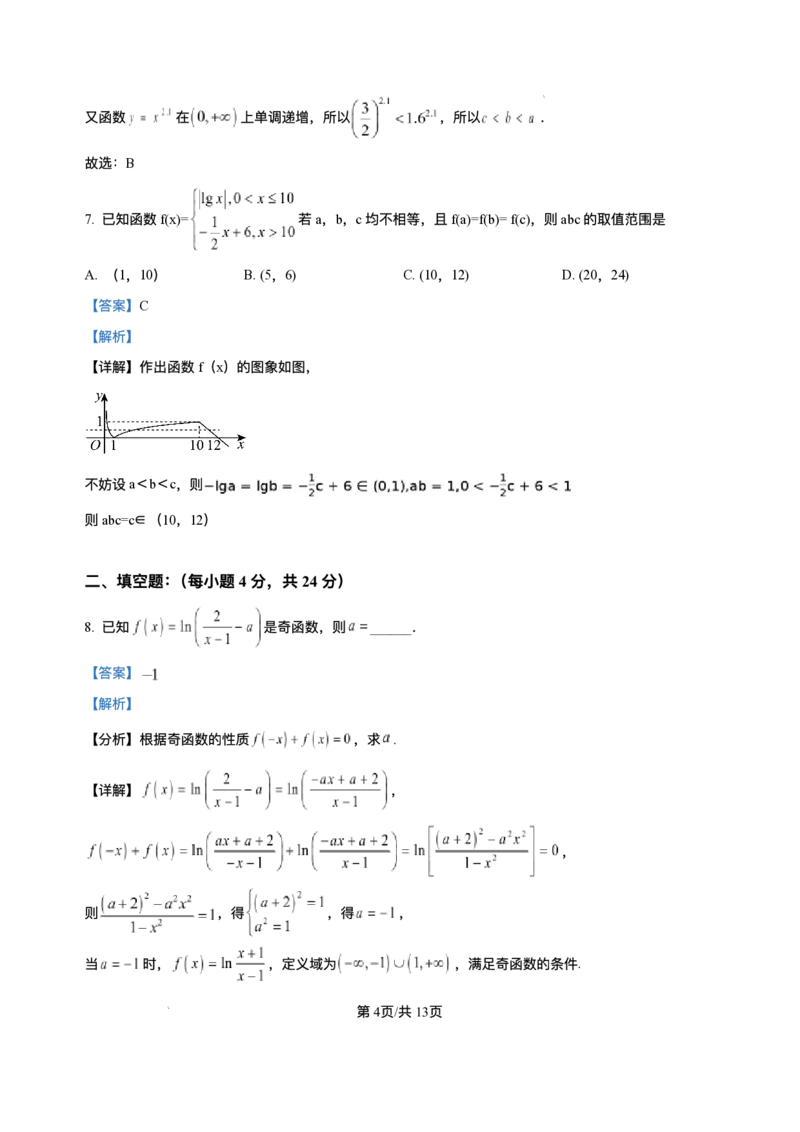
7. 已知函数f(x)= 若a,b,c均不相等,且f(a)=f(b)=f(c),则abc的取值范围是
A. (1,10) B.(5,6) C.(10,12) D.(20,24)
【答案】C
【解析】
【详解】作出函数f(x)的图象如图,
不妨设a<b<c,则
则abc=c∈(10,12)
⼆、填空题:(每⼩题4分,共24分)
8. 已知 是奇函数,则 ______.
【答案】
【解析】
【分析】根据奇函数的性质 ,求 .
【详解】 ,
,
则 ,得 ,得 ,
当 时, ,定义域为 ,满⾜奇函数的条件.
第4⻚/共13⻚
学科⽹(北京)股份有限公司所以 .
故答案为:
9. 已知 为第四象限⻆, 为其终边上的⼀点,且 ,则实数 _________
【答案】
【解析】
【分析】根据三⻆函数的定义,结合 为第四象限⻆求解即可.
【详解】由题知, ,解得 ,
⼜ 为第四象限⻆,所以 ,所以 .
故答案为:
10. 已知扇形的圆⼼⻆为3rad,⾯积为24,则该扇形的弧⻓为___________.
【答案】12
【解析】
【分析】由扇形的圆⼼⻆与⾯积求得半径再利⽤弧⻓公式即可求弧⻓.
【详解】设该扇形的弧⻓为 ,圆⼼⻆为 ,半径为 ,
所以由 ,即 ,解得 ,
所以 .
故答案为:12.
11. 计算: _________
【答案】
【解析】
【分析】利⽤指数幂的运算法则化简.
【详解】因为 , ,
所以 .
第5⻚/共13⻚
学科⽹(北京)股份有限公司故答案 :
12. 若 ,则 取得最⼩值时, __________.
【答案】
【解析】
【分析】先根据对数运算的性质计算出 与 的关系式,再利⽤乘“ 1” 法与基本不等式计算即可.
【详解】由
可整理得 ,得 ,
所以 ,
当且仅当 即 时取等号,结合 ,解得 ,
故答案为: .
13. 已知函数 ,若函数 满⾜:对于任意的 , ,当
时,都有 ,则实数 的取值范围是_____________________
【答案】
【解析】
【分析】根据题中条件,将问题转化为 为减函数,即可根据分段函数的单调性求解.
【详解】由 ,即 ,对于任意的 ,当 时
成⽴,
所以函数 是R上的减函数,
⼜ ,
第6⻚/共13⻚
学科⽹(北京)股份有限公司所以 ,解得 .
则实数 的取值范围是 ,
故答案为:
三、解答题:(本⼤题共4⼩题,共65分)
14. 计算:
(1)已知 第⼆象限⻆, ,求 ,
(2)已知 ,
(ⅰ)求 的值;
(ⅱ)求 的值.
【答案】(1)
(2)(ⅰ) ;(ⅱ)
【解析】
【分析】(1)利⽤同⻆三⻆函数的关系解⽅程组,再根据⻆的范围求解;
(2)(ⅰ)利⽤⻬次化思想求出 ,再利⽤⻬次化思想化简;(ⅱ)根据 以及⻬
次化思想化简.
【⼩问1详解】
因为 , ,
得 或 ,
第7⻚/共13⻚
学科⽹(北京)股份有限公司⼜ 为第⼆象限⻆,所以 ;
【⼩问2详解】
因为 ,所以 ,
(ⅰ) ;
(ⅱ) .
15. 已知函数 ,其中 且 .
(1)求 的值和函数 的定义域;
(2)判断并证明函数 的奇偶性;
(3)求不等式 的解集.
【答案】(1) ,定义域为 ;
(2) 为奇函数,证明⻅解析;
(3) .
【解析】
【分析】(1)由题设及对数运算性质可得 ,即可得参数值,进⽽求定义域;
(2)奇偶性定义求证函数奇偶性;
(3)根据解析式判断对数复合函数的单调性,再由单调性求解集.
【⼩问1详解】
由题设 ,可得 ,
⼜ ,故 ,则 ,
所以 ,即定义域为 .
【⼩问2详解】
第8⻚/共13⻚
学科⽹(北京)股份有限公司为奇函数,证明如下:
由(1)知:定义域关于原点对称,且 ,
所以 为奇函数.
【⼩问3详解】
由 ,⽽ 在 上递减, 在定义域上递增,
所以 在 上递减,且 ,
故 ,有 ,结合定义域知:解集为 .
16.
(1)若不等式 对于 恒成⽴,求实数k的取值范围;
(2)若函数 ( , )在区间 上单调递减,求实数a的取值范围;
(3)已知不等式 对满⾜ 的⼀切实数 恒成⽴求 的取值范围;
(4)你认为解决恒成⽴问题的本质是什么?
【答案】(1)
(2)
(3)
(4)将不等式的恒成⽴问题,转化为函数的最值问题,数形结合是解决恒成⽴问题的有效⽅法.
【解析】
【分析】(1)将不等式转化为 ,不等式恒成⽴转化为 ,求 的最⼩值即可
求出答案;
(2)根据复合函数的单调性及对数函数的定义域列不等式组即可求出答案;
(3)将不等式 化为 ,令 ,即得
第9⻚/共13⻚
学科⽹(北京)股份有限公司到关于 的函数,对 进⾏分类讨论,结合题意即可得到答案.
(4)对恒成⽴问题进⾏概括即可得到答案.
【⼩问1详解】
因为 ,所以不等式 可化为 ,
即 对任意 恒成⽴,
令 ,
所以 ,当且仅当 时等号成⽴,
即 的最⼩值为 ,所以 ,
所以实数k的取值范围为 .
【⼩问2详解】
因为 且 ,所以函数 在定义域上单调递减,
根据复合函数的单调性及对数函数的定义域,由题意可得 ,解得 ,
所以实数a的取值范围为 .
【⼩问3详解】
不等式 可化为 ,
令 ,
当 时, ,满⾜题意,
当 时, ,不满⾜题意,
当 时,函数 在定义域上单调递增,
由题意可得 ,解得 ,
第10⻚/共13⻚
学科⽹(北京)股份有限公司当 时,函数 在定义域上单调递减,
由题意可得 ,解得 ,
综上, 的取值范围为 .
【⼩问4详解】
将不等式的恒成⽴问题,转化为函数的最值问题,数形结合是解决恒成⽴问题的有效⽅法.
第Ⅱ卷 提⾼题(共18分)
17. 已知 .
(1)求证: ;
(2)判断 的单调性,并⽤单调性的定义证明;
(3)当 时, 恒成⽴,求实数 的取值范围.
【答案】(1)证明⻅解析;
(2) 在 上单调递增,证明⻅解析;
(3)
【解析】
【分析】(1)根据函数解析式,分别计算 的表达式,即可证明结论;
(2)结合函数解析式判断其单调性,利⽤函数单调性定义即可证明;
(3)判断函数 奇偶性, ,转化成 对于 恒成⽴,利⽤函数单调性即可
求解.
【⼩问1详解】
由题意可知 ;
,
第11⻚/共13⻚
学科⽹(北京)股份有限公司故 .
【⼩问2详解】
由题意得 ,其定义域为 ,
在 上单调递增,
证明:任取 ,不妨设 ,
,
因为 ,故 ,
⼜ ,故 ,即得 ,
故 在 上单调递增;
【⼩问3详解】
由题意知 的定义域为 , ,即 为奇函数;.
所以
等价于 ,⼜ 在 上单调递增;
所以 在 时恒成⽴,
令
则 ,
由对勾函数 的单调性可知其在 单调递增,
当 时, ,
所以 ,
即实数 的取值范围是
第12⻚/共13⻚
学科⽹(北京)股份有限公司第13⻚/共13⻚
学科⽹(北京)股份有限公司