文档内容
宁德市2023-2024学年度第二学期期末高一质量检测
数学参考答案及评分标准
说明:
一、本解答指出了每题要考查的主要知识和能力,并给出了一种或几种解法供参考,如果
考生的解法与本解法不同,可根据试题的主要考查内容比照评分标准制定相应的评分
细则.
二、对计算题,当考生的解答在某一部分解答未改变该题的内容和难度,可视影响的程度
决定后继部分的给分,但不得超过该部分正确解答应给分数的一半;如果后继部分的
解答有较严重的错误,就不再给分.
三、解答右端所注分数,表示考生正确做到这一步应得的累加分数.
四、只给整数分数,选择题和填空题不给中间分.
一、单项选择题: 本题共8小题,每小题5分,共40分. 在每小题给出的四个选项中,只
有一个选项是符合题目要求的.
1. C 2.A 3.D 4.D 5. B 6.C 7.C 8.B
第8题解析:
由 可得, ,
所以 .
因为 为钝角,所以 ,且 不共线,
所以 ,即 ,且 .
当 时,有 且 ,所以 可取2,4,5,6;
当 时,有 , 可取5,6;
当 , , , 时, ,此时无解.
综上所述,满足条件的 有6种可能.
又先后抛掷两次,得到的样本点数共36种,
所以 为钝角的概率
二、多项选择题:本题共3小题,每小题6分, 共18分. 在每小题给出的选项中有多项符
合题目要求,全部选对的得6分,部分选对的得部分分,有选错的得0分)
9. AD 10. ACD 11. AC
第11题解析:
对于A .该“刍童”的表面积为 ,所以正确
对于B .由轴截面的等腰梯形 可知,其高 ,如图所示:
高二数学参考答案 第1 页 共8页
学学学科科科网网网(((北北北京京京)))股股股份份份有有有限限限公公公司司司能够被完整放入该“刍童”内的圆台的最大的体积为 ,所以不正确
对于C .该“刍童”的外接球的球心到平面 的距离为 ,而平面 的外接圆
的圆心恰为线段 的中点,故该“刍童”的外接球的球心到平面 的距离为 ,所
以正确.
对于D ,若正四面体在此容器内部可以任意转动,则正四面体的外接球可以放进容器,棱
长为 的正四面体的外接球直径为 ,由轴截面的等腰梯形 可知,其高
,如下图所示:
可知此棱台可放入的最大球的直径为 ,小于正四面体的外接球直径,
故不可以在此空心棱台容器内部任意转动,所以D不正确.
故选:AC
三、填空题:(本大题共3小题,每小题5分,共15分. 把答案填在答题卡的相应位置)
12. 2800 13. 14.
第14题解析:
如图示,可知: 是边长为2的菱形,且 ,
,所以
四、解答题:本大题共5小小题,共77分. 解答应写出文字说明,证明过程或演算步骤
.
15. (本小题满分13分)
高二数学参考答案 第2 页 共8页
学学学科科科网网网(((北北北京京京)))股股股份份份有有有限限限公公公司司司(1)因为 ,································································2分
所以 ·····························································································4分
所以 ······························································6分
(2)因为 ···························································7分
·················································································9分
所以 ······················································································11分
所以 ························································································13分
16. (本小题满分15分)
解:(1)证明:由于底面 为矩形,所以 ··································1分
又有 平面 , 平面 ,所以 ···································4分
因为 ,所以 平面 ·······················································6分
因为 平面 ,所以平面 平面 ·······································7分
(2)解:由于 即 为异面直线 和 所成角所成的角.·············8分
因为异面直线 和 所成角的正切值为 ,
由于 平面 所以
所以在 中, ,所以 ····················································9分
由于 是边长为4的正三角形,取 的中点 ,连接 ,
所以 ···········································································10分
因为平面 平面 , 平面 ,所以 平面 .···········11分
取 的中点 ,连接 , , , ,所以
所以 为二面角 的平面角,··················································13分
在 中, ,所以 . ·································14分
所以 为二面角 的平面角 ·················································15分
高二数学参考答案 第3 页 共8页
学学学科科科网网网(((北北北京京京)))股股股份份份有有有限限限公公公司司司17.(本小题满分15分)
解:(1)根据正弦定理可得: , ················2分
··············································3分
因为 , ··········································································4分
所以 ··························································································5分
即 ···································································································7分
法二:根据余弦定理可得 ················2分
即 ,························································································3分
所以 ··························································································4分
因为 ,······················································································5分
所以 .······························································································7分
(2)解:因为 ,
所以 ····························································8分
解得 ·····························································································9分
因为 平分
在 中根据正弦定理得:
在 中根据正弦定理得:
所以 ,······················································································11分
高二数学参考答案 第4 页 共8页
学学学科科科网网网(((北北北京京京)))股股股份份份有有有限限限公公公司司司所以 ,·························································································12分
所以 ···················13分
所以 ,··············································14分
解得 ,即 ;·································································15分
法二:因为 ,
所以 ····························································8分
解得 ·····························································································9分
因为 平分
所以 ·······························12分
整理得: ················································································14分
即 ····························································································15分
18. (本小题满分17分)
(1)根据频率分布直方图有,男生成绩样本数据的平均数
························4分
所以男生成绩样本数据的平均数为71.(列式正确,计算错误扣1分)
(2)在区间 和 内的男生成绩样本数据分别有4个和2个,···········5分
分别用 和 表示,则在这6个数据中随机抽取两个的样本空间 包含的样本点
有 ,
,
个数为 ,····················································································7分
高二数学参考答案 第5 页 共8页
学学学科科科网网网(((北北北京京京)))股股股份份份有有有限限限公公公司司司记事件 “这两个样本来自同一区间”,
则事件 包含的样本点有
个数为 ,······················································································9分
所以 ;·············································································10分
(3)设男生成绩样本数据为 , ,…, ,其平均数为71,方差为
女生成绩样本数据为 , ,…, ,其平均数为 ,
方差为 ;总样本的平均数为 ,方差为 .··········································11分
由按比例分配分层随机抽样总样本平均数与各层样本平均数的关系,
得 .·············································································13分
················································14分
·············································15分
.··································································································17分
所以总样本的平均数和方差分别为 和 .
19.(本小题满分17分)
(1)解:由于 是正方体,
两直线 , 与面 所成的角相等
即 ,由于 ·········································1分
法1: ,即 ····································3分
法2:所以 ,又有 是 的中点, ········3分
即 ,
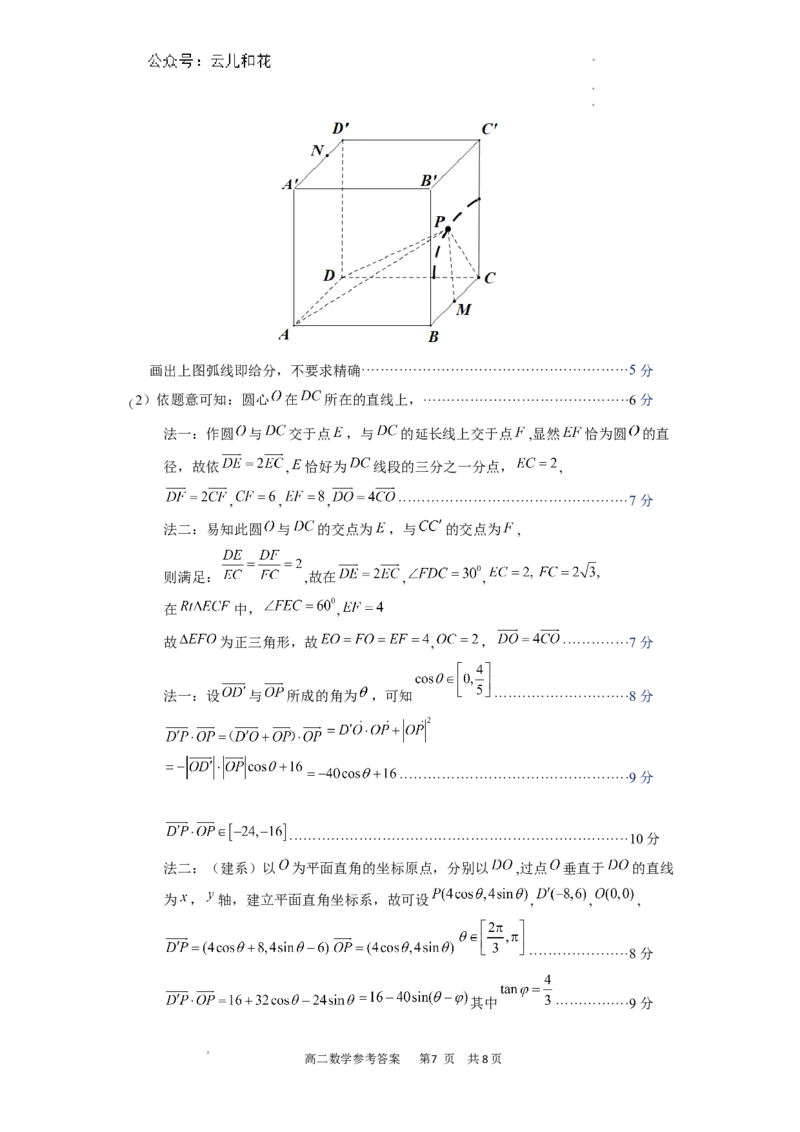
依题意平面内点 到两定点 距离之比为2,故点 的轨迹是圆,
而点 是正方体表面 上一动点(包括边界),
即点 的轨迹是一段阿波罗尼斯圆的弧.··················································4分
高二数学参考答案 第6 页 共8页
学学学科科科网网网(((北北北京京京)))股股股份份份有有有限限限公公公司司司画出上图弧线即给分,不要求精确·························································5分
(2)依题意可知:圆心 在 所在的直线上,············································6分
法一:作圆 与 交于点 ,与 的延长线上交于点 ,显然 恰为圆 的直
径,故依 , 恰好为 线段的三分之一分点, ,
, , , ·················································7分
法二:易知此圆 与 的交点为 ,与 的交点为 ,
则满足: ,故在 , ,
在 中, ,
故 为正三角形,故 , , ··············7分
法一:设 与 所成的角为 ,可知 ·····························8分
·················································9分
·········································································10分
法二:(建系)以 为平面直角的坐标原点,分别以 ,过点 垂直于 的直线
为 , 轴,建立平面直角坐标系,故可设 , , ,
·····················8分
其中 ················9分
高二数学参考答案 第7 页 共8页
学学学科科科网网网(((北北北京京京)))股股股份份份有有有限限限公公公司司司故 ······································································10分
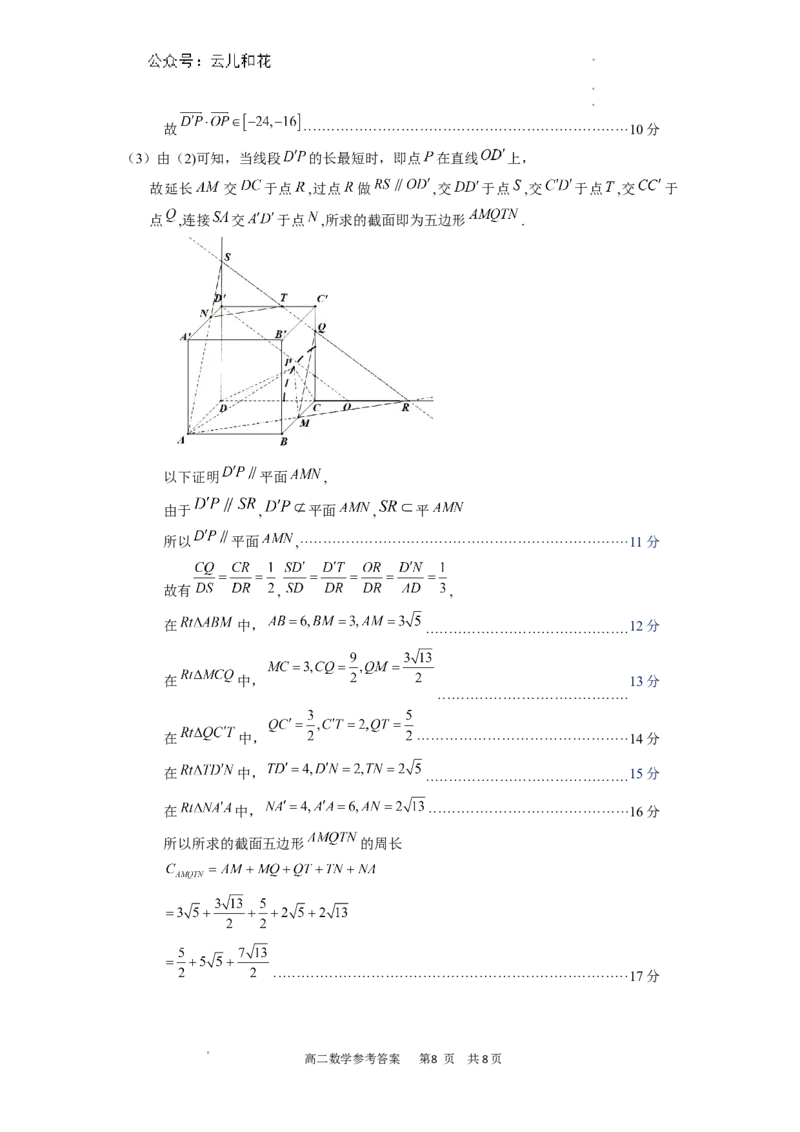
(3)由(2)可知,当线段 的长最短时,即点 在直线 上,
故延长 交 于点 ,过点 做 ,交 于点 ,交 于点 ,交 于
点 ,连接 交 于点 ,所求的截面即为五边形 .
以下证明 平面 ,
由于 , 平面 , 平
所以 平面 ,·······································································11分
故有 , ,
在 中, 12分
············································
在 中, 13分
·········································
在 中, ·············································14分
在 中, 15分
············································
在 中, ···········································16分
所以所求的截面五边形 的周长
············································································17分
高二数学参考答案 第8 页 共8页
学学学科科科网网网(((北北北京京京)))股股股份份份有有有限限限公公公司司司