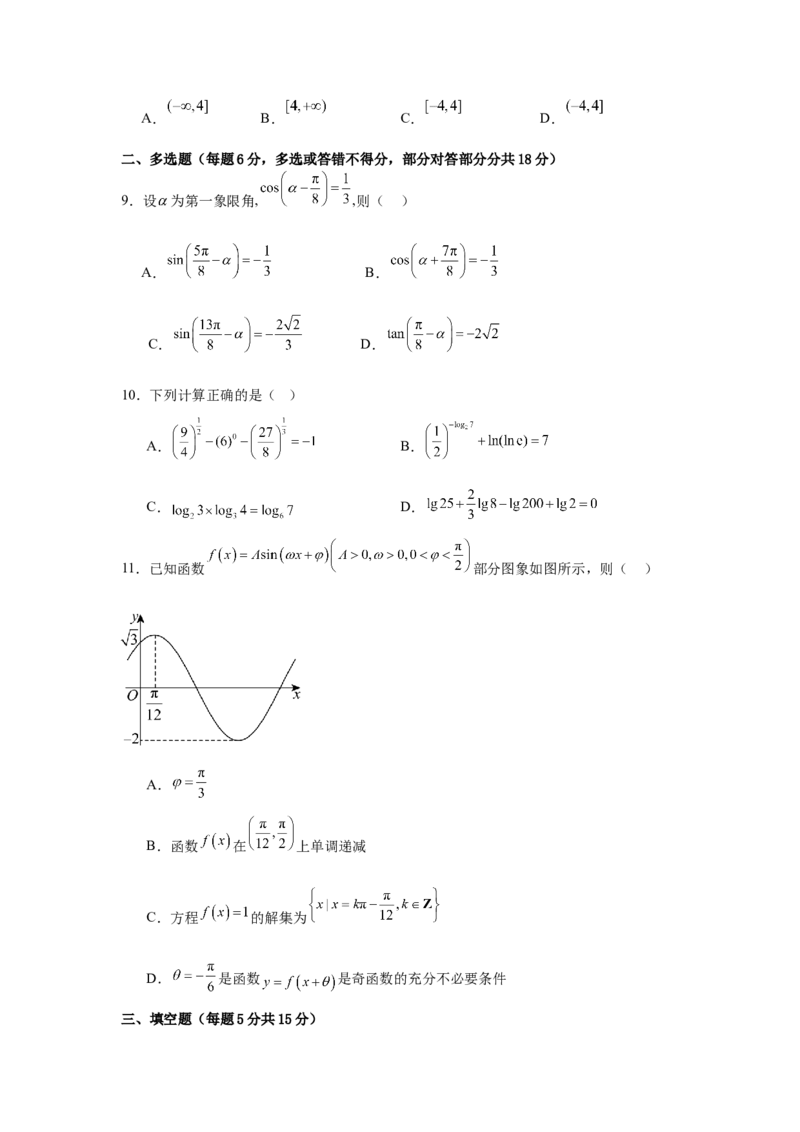文档内容
独山中学2024-2025学年度第二学期2月月考高一数学考试卷
一、单选题(每题5分共40分)
1.设集合A={x|x2–4≤0},B={x|2x+a≤0},且A∩B={x|–2≤x≤1},则a=( )
A.–4 B.–2 C.2 D.4
2. ( )
A. B. C. D.
3. ( )
A. B. C. D.1
4.设 , ,那么 是( )
A.奇函数且在 上是增函数 B.偶函数且在 上是减函数
C.奇函数且在 上是减函数 D.偶函数且在 上是增函数
5.已知某扇形的周长为5cm,面积为 ,则该扇形圆心角的弧度数是( )
A. B.3 C. 或3 D.
6.已知角 的终边上有一点 ,则 ( )
A. B.2 C. D.3
7.已知 , , ,则( )
A. B. C. D.
8.已知函数 在 上单调递减,则实数 的取值范围( )A. B. C. D.
二、多选题(每题6分,多选或答错不得分,部分对答部分分共18分)
9.设 为第一象限角, ,则( )
A. B.
C. D.
10.下列计算正确的是( )
A. B.
C. D.
11.已知函数 部分图象如图所示,则( )
A.
B.函数 在 上单调递减
C.方程 的解集为
D. 是函数 是奇函数的充分不必要条件
三、填空题(每题5分共15分)12.函数 的定义域是-----------.
13.若 ,则 ----------.
14.若 ,则 ------------.
四、解答题
15(第一小题6分,第二小题7分共13分).
记关于x的不等式 的解集为P,不等式|x-1|≤1的解集为Q.
(1)若a=3,求P;
(2)若Q P,求正数a的取值范围.
⊆
16(第一小题7分,第二小题8分共15分).
(1)已知角 终边上一点 ,求 的值;
(2)化简求值:
17第一小题7分,第二小题8分共15分).
已知函数 是定义在 上的奇函数,且当 时, .
(1)求当 时, 的解析式;
(2)求 在 上的值域.
18(第一小题8分,第二小题9分共17分).
甲厂以x 千克/小时的速度匀速生产某种产品(生产条件要求 ),每小时可获
得利润是 元.(1)要使生产该产品2小时获得的利润不低于3000元,求x的取值范围;
(2)要使生产900千克该产品获得的利润最大,问:甲厂应该选取何种生产速度?并求最大
利润.
19(第一小题4分,第二小题6分,第三小题7分共17分).
已知 ,
(1)求 的值;
(2)求 的值;
(3)求 的值.
参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 B D D D C B D C BD ABD
题号 11
答案 ABD
12.
13.
14.
15.(1){x|-1<x<3}
(2)(2,+∞)
16.(1) ;(2)2
17.(1)
(2)18.(1) (2) 时, 元
19.(1)
(2)
(3)
【解】(1)由于 ,所以 ,
又 得 ,
解得 或 (舍去),
故
(2)
(3)