文档内容
格致课堂
8.3.1 棱柱、棱锥、棱台的表面积和体积
(用时45分钟)
【选题明细表】
知识点、方法 题号
棱柱、棱锥、棱台的表面积和体积 1,2,3,4,5,6,7,8,9,10,11,12
基础巩固
1.将一个正方体截去四个角后,得到一个四面体,这个四面体的体积是原正方体体积的( )
A. B. C. D.
【答案】C
【解析】
将正方体 截去四个角后得到一个四面体 ,
设正方体的棱长为 ,
则 ,
四面体 的体积 ,
所以这个四面体的体积是原正方体体积的 .
故选:C.
2.若棱台上、下底面的对应边之比为1∶2,则上、下底面的面积之比是 ( )
A.1∶2 B.1∶4 C.2∶1 D.4∶1格致课堂
【答案】B
【解析】由棱台的概念知,上、下两底面是相似的多边形,故它们的面积之比等于对应边长之比的平方,
故为1∶4. 选B.
3.将两个棱长为 的正方体铜块熔化后铸成底面边长为 的正四棱柱,则该四棱柱的高为( )
A.8 cm B.80 cm C.40 cm D.
【答案】B
【解析】∵正方体的棱长为 ,
∴两个正方体的体积V=2×10×10×10=2000cm3,
设熔化后铸成一个正四棱柱的铜块的高为acm,
则5×5×a=2000
解得a=80cm
故选:B.
4.如图,已知正六棱柱的最大对角面的面积为1m2,互相平行的两个侧面的距离为1m,则这个六棱柱的
体积为( )
A. B. C.1m3 D.
【答案】B
【解析】设正六棱柱的底面边长为 m,高为 m,则 , ,解得 .
所以六棱柱的体积 .
故选:B.格致课堂
5.若正方体的棱长为 ,则以该正方体各个面的中心为顶点的凸多面体的体积为( )
A. B. C. D.
【答案】B
【解析】所求八面体体积是两个底面边长为1,高为 , 的四棱锥的体积和,一个四棱锥体积V=
1
,故八面体体积V=2V= ,故选B.
1
6.棱长为2的正四面体的表面积是_____.
【答案】 .
【解析】每个面的面积为 ,∴正四面体的表面积为 .
7.如图,长方体 的体积是120,E为 的中点,则三棱锥E-BCD的体积是_____.
【答案】10.
【解析】因为长方体 的体积为120,
所以 ,
因为 为 的中点,格致课堂
所以 ,
由长方体的性质知 底面 ,
所以 是三棱锥 的底面 上的高,
所以三棱锥 的体积 .
8.已知四棱台的上、下底面分别是边长为4和8的正方形,侧面是腰长为8的等腰梯形,求该四棱台的表
面积.
【答案】
【解析】如图,
在四棱台 中,
过 作 ,垂足为 ,
在 中, , ,
故 ,
所以 ,
故四棱台的侧面积 ,
所以四棱台的表面积 .格致课堂
能力提升
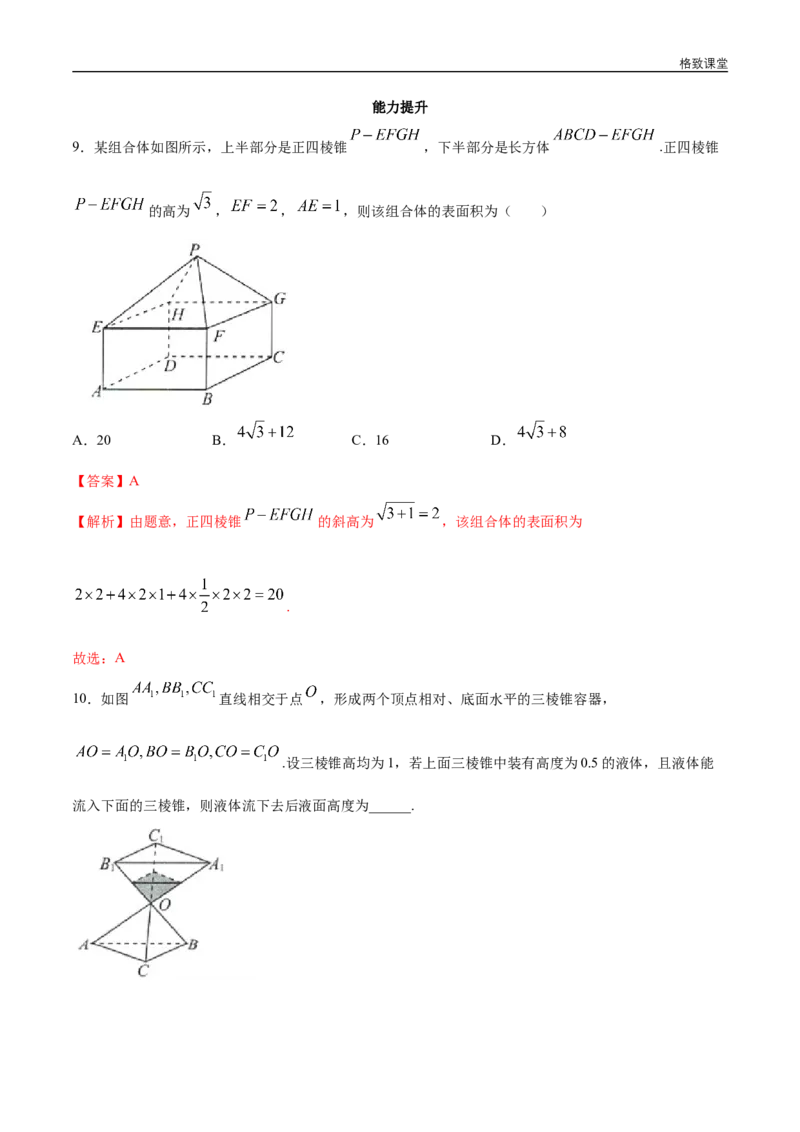
9.某组合体如图所示,上半部分是正四棱锥 ,下半部分是长方体 .正四棱锥
的高为 , , ,则该组合体的表面积为( )
A.20 B. C.16 D.
【答案】A
【解析】由题意,正四棱锥 的斜高为 ,该组合体的表面积为
.
故选:A
10.如图 直线相交于点 ,形成两个顶点相对、底面水平的三棱锥容器,
.设三棱锥高均为1,若上面三棱锥中装有高度为0.5的液体,且液体能
流入下面的三棱锥,则液体流下去后液面高度为______.格致课堂
【答案】 .
【解析】液体部分的体积为三棱锥体积的 ,流下去后,液体上方空出的三棱锥的体积为三棱锥体积的 .
设空出三棱锥的高为 ,则 ,所以 ,所以液面高度为 .
故答案为:
11.如图,在几何体 中, , , ,侧棱 , , 均垂直于底面
, , , ,求该几何体的体积.
【答案】
【解析】由题意可知 为直角三角形,且 为直角,
如图,取 ,连接 , , ,
因为 , , ,
所以三棱柱 的体积为 ,
因为 , , , ,格致课堂
所以 , , , ,
所以四棱锥 的体积为 ,
所以所求几何体的体积为 .
素养达成
12.已知一个三棱台的上、下底面分别是边长为20和30的正三角形,侧面是全等的等腰梯形,且侧面面
积等于上下底面面积之和,求棱台的高和体积.
【答案】 ; .
【解析】如图所示,
在三棱台 中,
, 分别为上、下底面的中心,
, 分别是 , 的中点,
连接 , , , ,
则点 , 分别在 , 上,
是等腰梯形 的高,记为 ,
所以 ,
上、下底面面积之和为 ,格致课堂
由 ,得 ,所以 ,
又 , ,
记棱台的高为 ,
则 ,
由棱台的体积公式,
得棱台体积 ,
计算得棱台体积 .