文档内容
格致课堂
8.3.2 圆柱、圆锥、圆台、球的表面积和体
积
一、选择题
1.若圆锥的高等于底面直径,则它的底面积与侧面积之比为
A.1∶2 B.1∶
C.1∶ D. ∶2
【答案】C
【解析】设圆锥底面半径为r,则高h=2r,∴其母线长l= r.∴S =πrl= πr2,S =πr故选C.
侧 底
2.(2017新课标全国Ⅲ理科)已知圆柱的高为1,它的两个底面的圆周在直径为2的同一个球的球面上,
则该圆柱的体积为
A. B.
C. D.
【答案】B
【解析】
绘制圆柱的轴截面如图所示,由题意可得: ,
结合勾股定理,底面半径 ,
由圆柱的体积公式,可得圆柱的体积是 ,故选B.格致课堂
3.圆柱的底面半径为1,母线长为2,则它的侧面积为( )
A. B. C. D.
【答案】D
【解析】圆柱的底面半径为r=1,母线长为l=2,
则它的侧面积为S =2πrl=2π×1×2=4π.
侧
故选:D.
4.圆台的上、下底面半径和高的比为 ,母线长为10,则圆台的侧面积为( ).
A.81π B.100π C.14π D.169π
【答案】B
【解析】设圆台上底半径为r,则其下底半径为4r,高为4r,结合母线长10,可求出r=2.然后由圆台侧面
积公式得, .
5.(多选题)一个圆柱和一个圆锥的底面直径和它们的高都与一个球的直径2R相等,下列结论正确的是
( )
A.圆柱的侧面积为 B.圆锥的侧面积为格致课堂
C.圆柱的侧面积与球面面积相等 D.圆柱、圆锥、球的体积之比为3:1:2
【答案】CD
【解析】依题意得球的半径为R,则圆柱的侧面积为 ,∴A错误;
圆锥的侧面积为 ,∴B错误;
球面面积为 ,∵圆柱的侧面积为 ,∴C正确;
, ,
,∴D正确.
故选:CD.
6.(多选题)如图所示, 的三边长分别是 , , ,过点C作 ,垂
足为D.下列说法正确的是( )
A.以 所在直线为轴,将此三角形旋转一周,所得旋转体的侧面积为15π
B.以 所在直线为轴,将此三角形旋转一周,所得旋转体的体积为36π
C.以 所在直线为轴,将此三角形旋转一周,所得旋转体的侧面积为25π格致课堂
D.以 所在直线为轴,将此三角形旋转一周,所得旋转体的体积为16π
【答案】AD
【解析】以 所在直线为轴旋转时,所得旋转体为底面半径为3,母线长为5,高为4的圆锥
∴侧面积为 ,体积为 ,∴A正确,B错误;
以 所在直线为轴旋转时,所得旋转体为底面半径为4,母线长为5,高为3的圆锥
侧面积为 ,体积为 ,∴C错误,D正确.
故选:AD.
二、填空题
7. 已知一个正方体的所有顶点在一个球面上,若这个正方体的表面积为18,则这个球的体积为____.
【答案】
【解析】
设正方体边长为 ,则 ,
外接球直径为 .
8.如图,若球 的半径为5,一个内接圆台的两底面半径分别为3和4(球心 在圆台的两底面之间),
则圆台的体积为______.格致课堂
【答案】
【解析】解:作经过球心的截面(如图),由题意得 , , ,则 ,
, ,
所以 .
9.已知圆柱的上、下底面的中心分别为 ,过直线 的平面截该圆柱所得的截面是面积为4的正
方形,则该圆柱的表面积为_______.
【答案】
【解析】由题意,圆柱的截面是面积为4的正方形,可得其边长为2,
可得圆柱的底面半径为 ,母线 ,
所以该圆柱的表面积为 。
10.一个球与一个正三棱柱的三个侧面和两个底面都相切,已知这个球的体积是 ,那么这个三棱柱
的底面边长为 ,体积是 .
【答案】
【解析】由球的体积公式,得 ,解得 ,所以正三棱柱的高h=2R=4.设正三棱柱的底面
边长为a,则其内切圆的半径为: ,得 ,所有该正三棱柱的体积为格致课堂
三、解答题
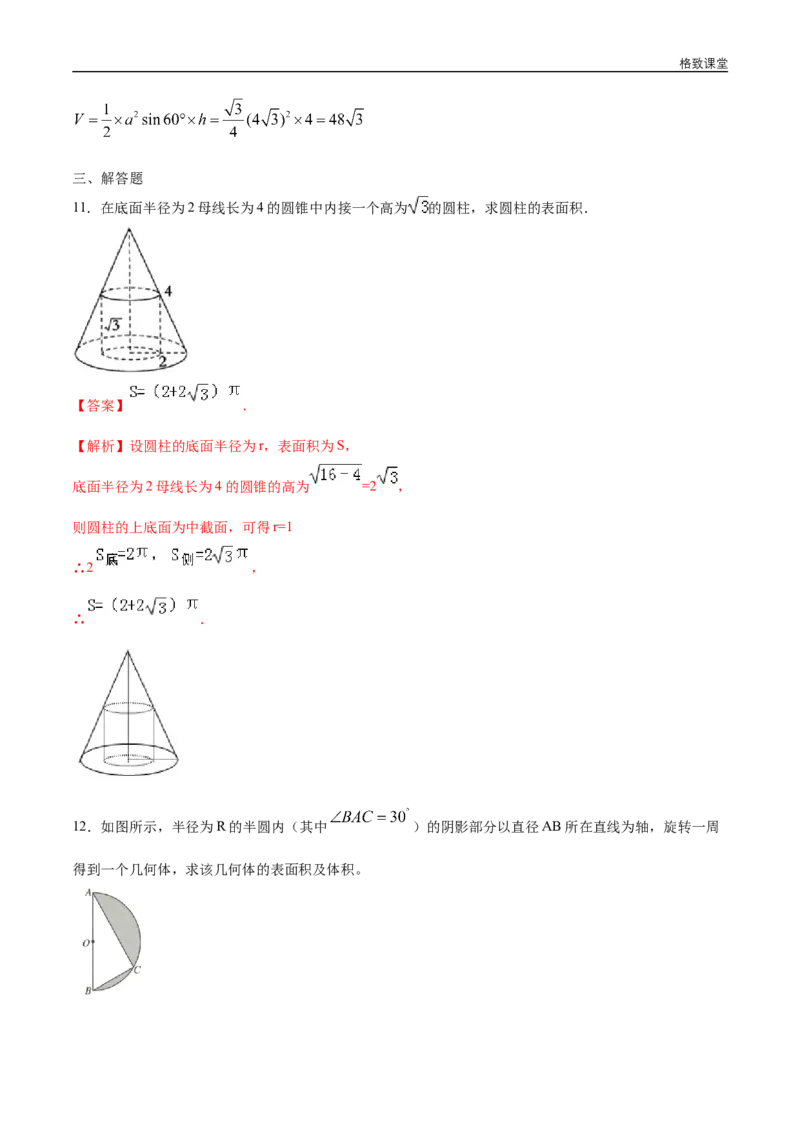
11.在底面半径为2母线长为4的圆锥中内接一个高为 的圆柱,求圆柱的表面积.
【答案】 .
【解析】设圆柱的底面半径为r,表面积为S,
底面半径为2母线长为4的圆锥的高为 =2 ,
则圆柱的上底面为中截面,可得r=1
∴2 ,
∴ .
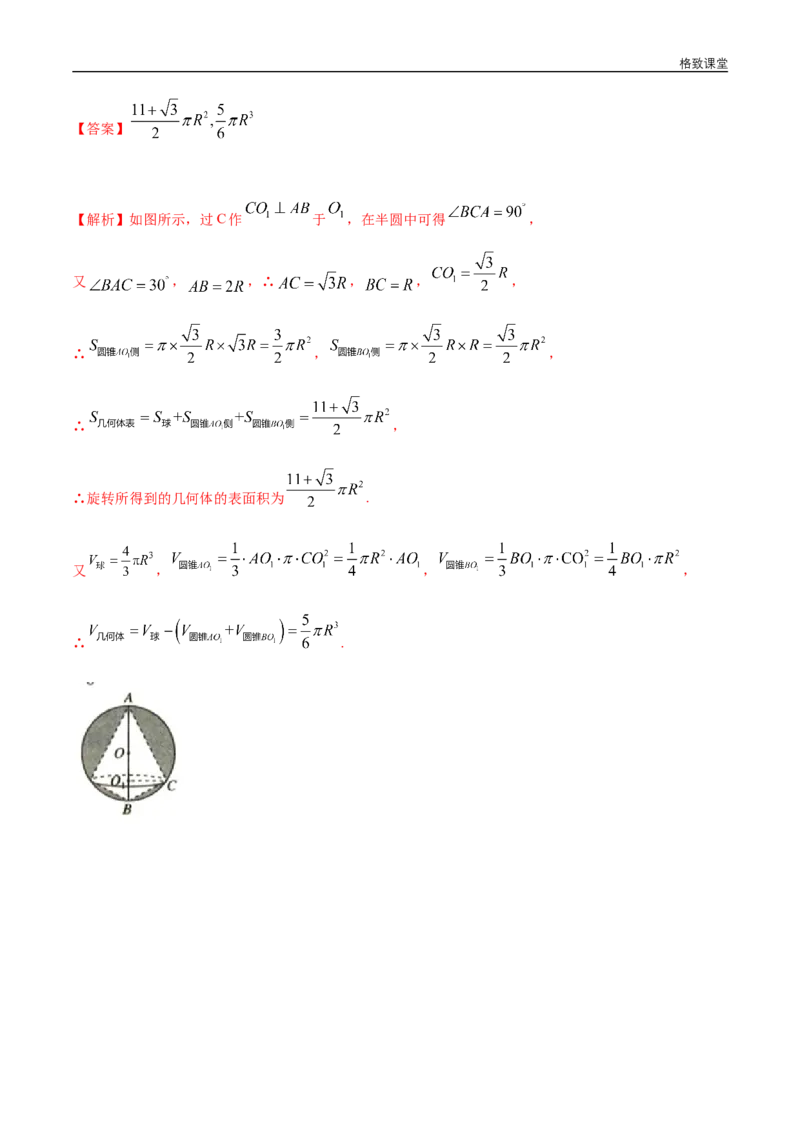
12.如图所示,半径为R的半圆内(其中 )的阴影部分以直径AB所在直线为轴,旋转一周
得到一个几何体,求该几何体的表面积及体积。格致课堂
【答案】
【解析】如图所示,过C作 于 ,在半圆中可得 ,
又 , ,∴ , , ,
∴ , ,
∴ ,
∴旋转所得到的几何体的表面积为 .
又 , , ,
∴ .