文档内容
格致课堂
8.6.2 直线与平面垂直
第1课时 直线与平面垂直的判定
(用时45分钟)
【选题明细表】
知识点、方法 题号
线面垂直的定义及判定定理的理解 1
线面垂直的判定及证明 2,4,8,12
直线与平面所成的角 3,6,9
综合问题 5,7,10,11
基础巩固
1.已知 和 是两条不同的直线, 和 是两个不重合的平面,那么下面给出的条件中,一定能推出
的是( )
A. ,且 B. ,且
C. ,且 D. ,且
【答案】B
【解析】A中, ,且 ,则 ,故A错误;
一条直线垂直于平面,则与这条平行的直线也垂直于这个平面,易知B正确;
C、D中, 或 或m与 相交均有可能,故C、D错误.
故选:B
2.如图所示的正方形 中, 分别是 , 的中点,现沿 , , 把这个正方
形折成一个四面体,使 , , 重合为点 ,则有( )格致课堂
A. 平面 B. 平面
C. 平面 D. 平面
【答案】A
【解析】由题意: , ,
, 平面
所以 平面 正确,D不正确;.
又若 平面 ,则 ,由平面图形可知显然不成立;
同理 平面 不正确;
故选:A
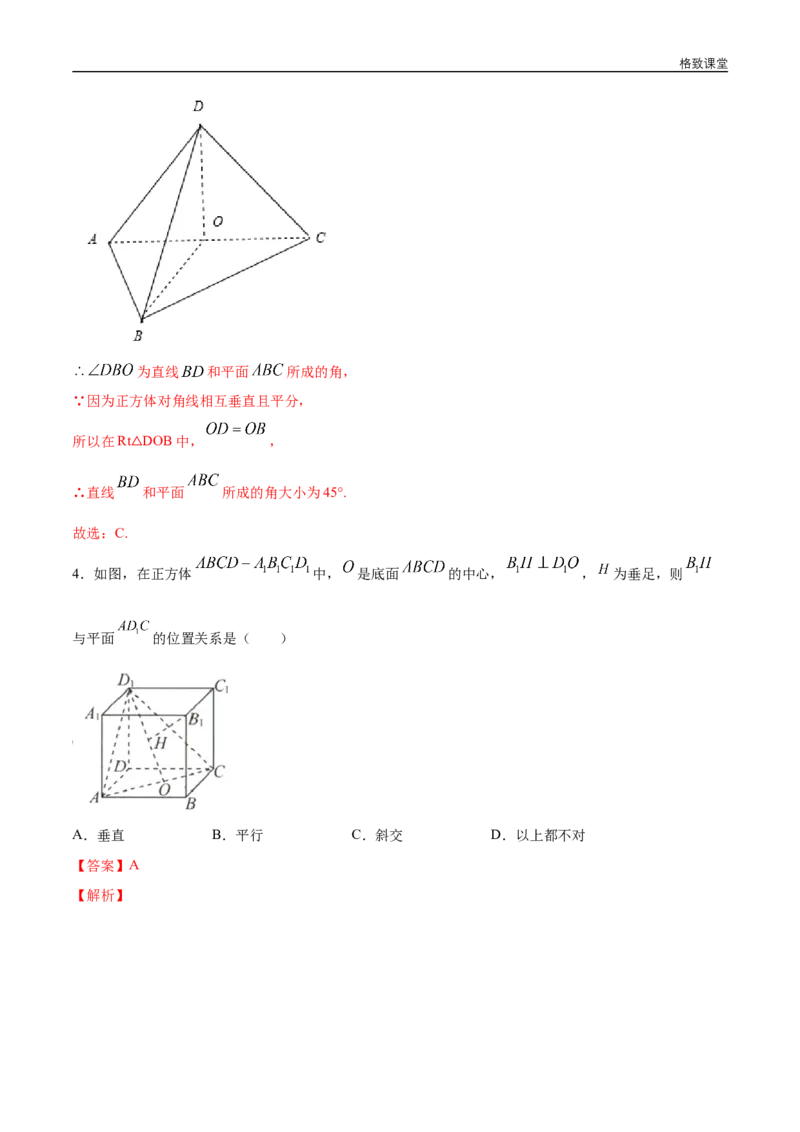
3.把正方形 沿对角线 折起,当以 四点为顶点的棱锥体积最大时,直线 和平面
所成的角的大小为( )
A.90° B.60 C.45° D.30°
【答案】C
【解析】记正方形 的对角线 与 交于点 ,
将正方形 沿对角线 折起后,如图,
当 平面 时,三棱锥 的体积最大.格致课堂
为直线 和平面 所成的角,
∵因为正方体对角线相互垂直且平分,
所以在Rt DOB中, ,
△
∴直线 和平面 所成的角大小为45°.
故选:C.
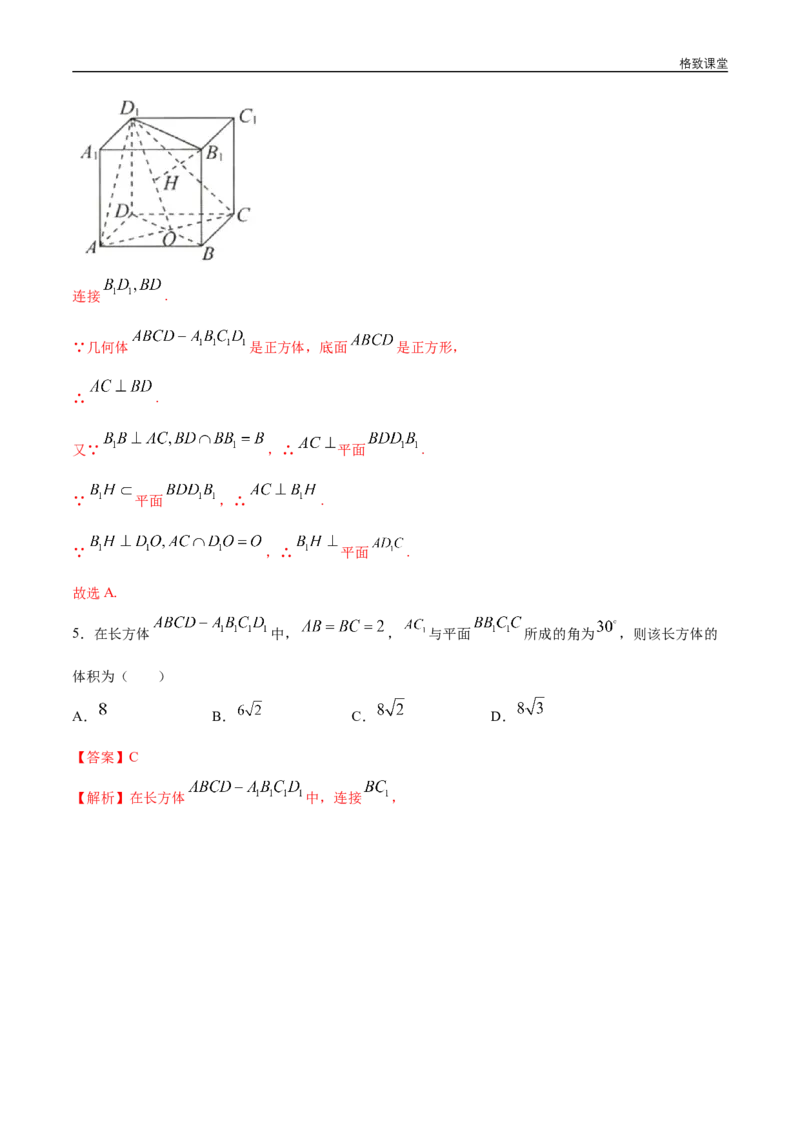
4.如图,在正方体 中, 是底面 的中心, , 为垂足,则
与平面 的位置关系是( )
A.垂直 B.平行 C.斜交 D.以上都不对
【答案】A
【解析】格致课堂
连接 .
∵几何体 是正方体,底面 是正方形,
∴ .
又∵ ,∴ 平面 .
∵ 平面 ,∴ .
∵ ,∴ 平面 .
故选A.
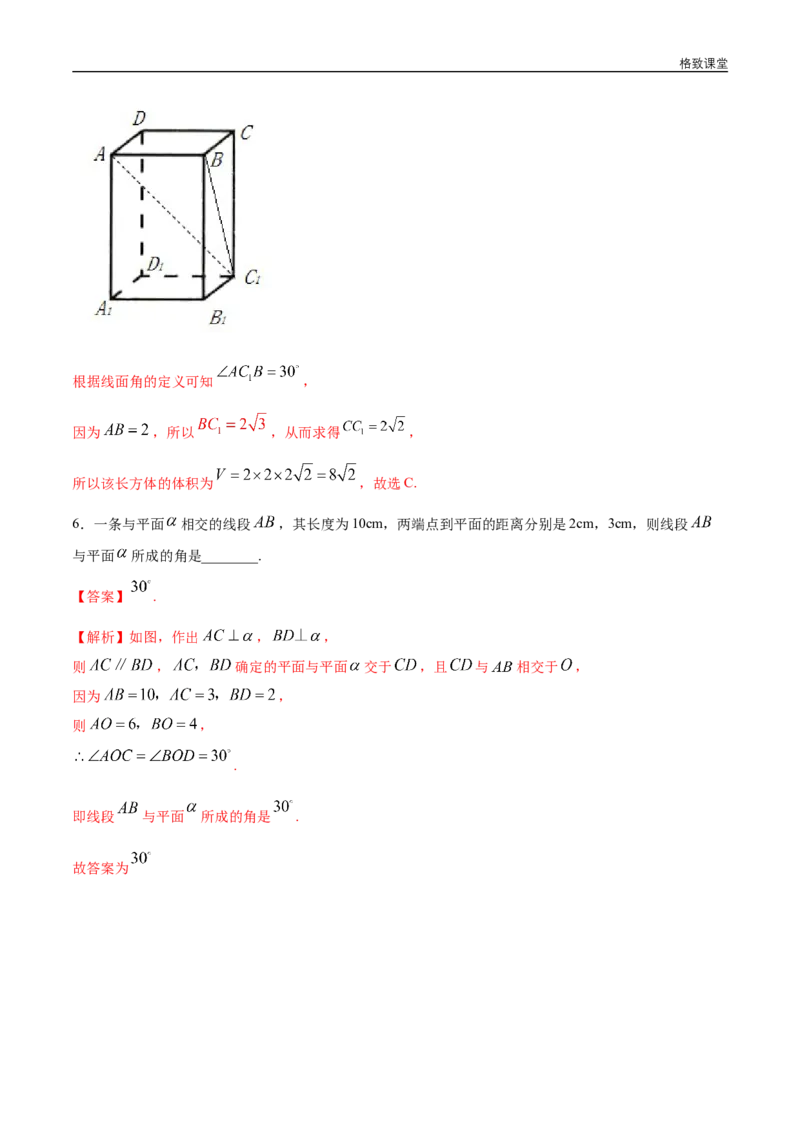
5.在长方体 中, , 与平面 所成的角为 ,则该长方体的
体积为( )
A. B. C. D.
【答案】C
【解析】在长方体 中,连接 ,格致课堂
根据线面角的定义可知 ,
因为 ,所以 ,从而求得 ,
所以该长方体的体积为 ,故选C.
6.一条与平面 相交的线段 ,其长度为10cm,两端点到平面的距离分别是2cm,3cm,则线段
与平面 所成的角是________.
【答案】 .
【解析】如图,作出 , ,
则 , 确定的平面与平面 交于 ,且 与 相交于 ,
因为 ,
则 ,
.
即线段 与平面 所成的角是 .
故答案为格致课堂
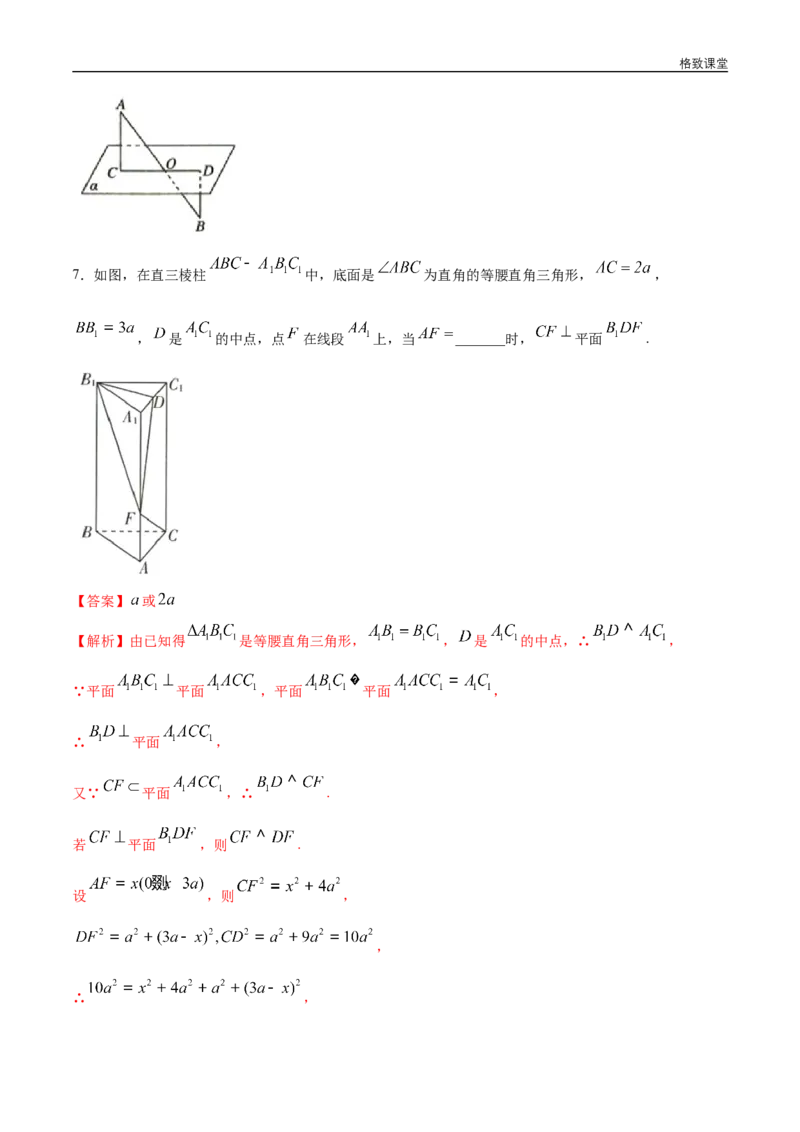
7.如图,在直三棱柱 中,底面是 为直角的等腰直角三角形, ,
, 是 的中点,点 在线段 上,当 _______时, 平面 .
【答案】 或
【解析】由已知得 是等腰直角三角形, , 是 的中点,∴ ,
∵平面 平面 ,平面 平面 ,
∴ 平面 ,
又∵ 平面 ,∴ .
若 平面 ,则 .
设 ,则 ,
,
∴ ,格致课堂
解得 或 .
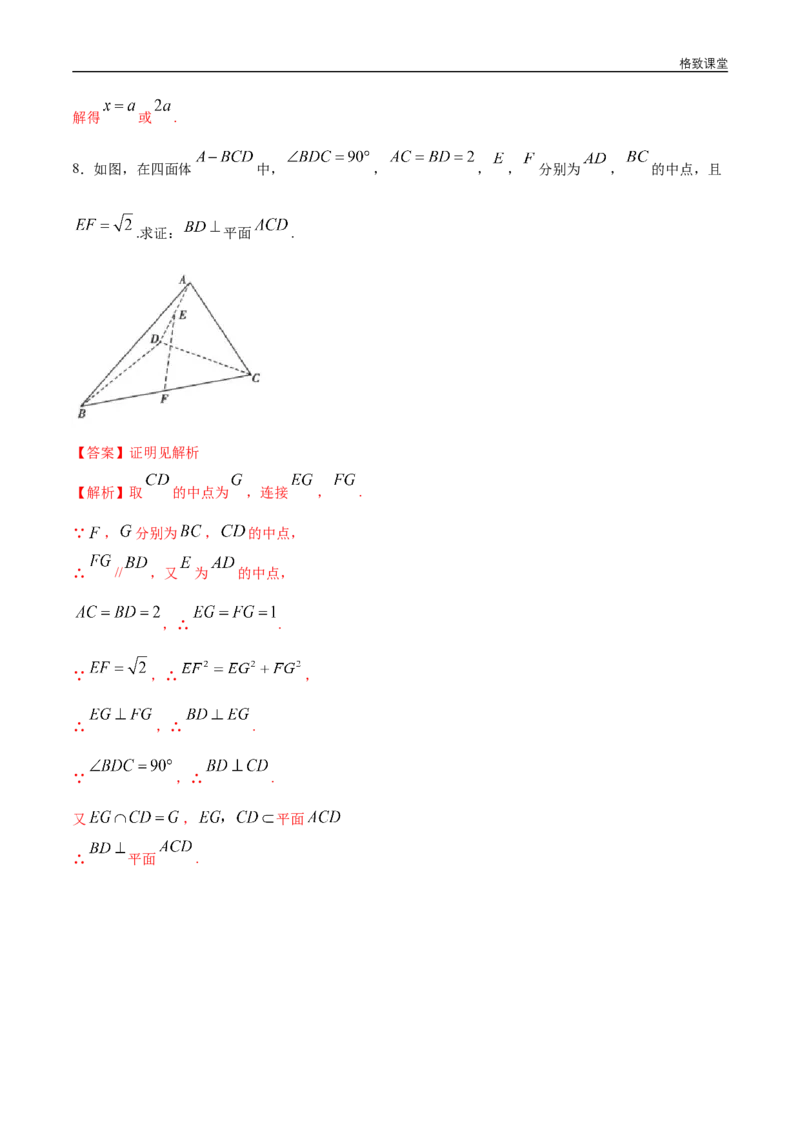
8.如图,在四面体 中, , , , 分别为 , 的中点,且
.求证: 平面 .
【答案】证明见解析
【解析】取 的中点为 ,连接 , .
∵ , 分别为 , 的中点,
∴ // ,又 为 的中点,
,∴ .
∵ ,∴ ,
∴ ,∴ .
∵ ,∴ .
又 , 平面
∴ 平面 .格致课堂
能力提升
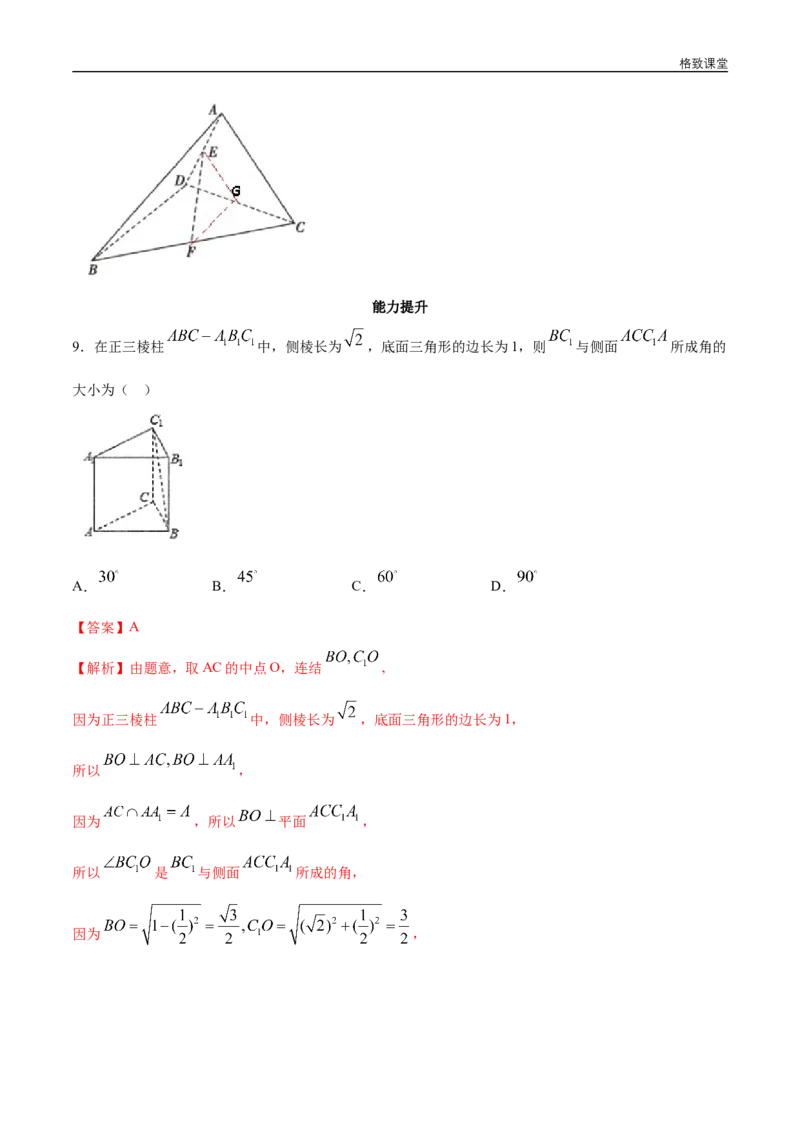
9.在正三棱柱 中,侧棱长为 ,底面三角形的边长为1,则 与侧面 所成角的
大小为( )
A. B. C. D.
【答案】A
【解析】由题意,取AC的中点O,连结 ,
因为正三棱柱 中,侧棱长为 ,底面三角形的边长为1,
所以 ,
因为 ,所以 平面 ,
所以 是 与侧面 所成的角,
因为 ,格致课堂
所以 ,
所以 , 与侧面 所成的角 .
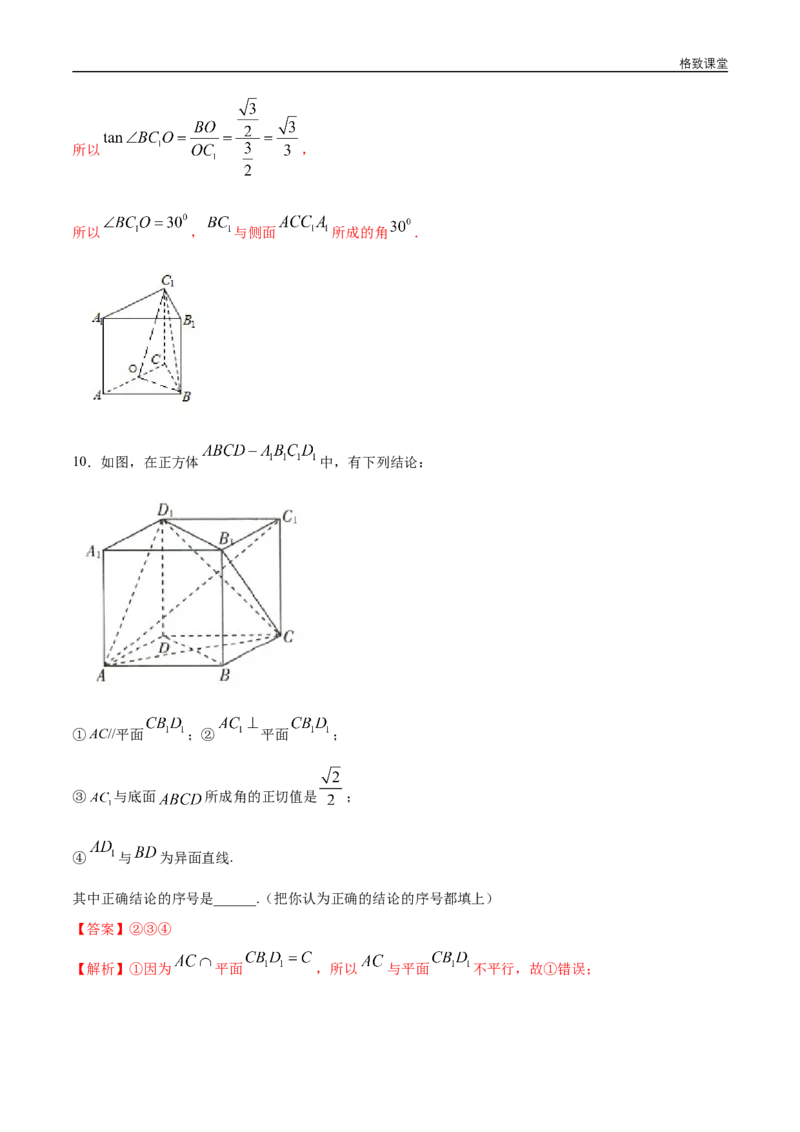
10.如图,在正方体 中,有下列结论:
①AC//平面 ;② 平面 ;
③ 与底面 所成角的正切值是 ;
④ 与 为异面直线.
其中正确结论的序号是______.(把你认为正确的结论的序号都填上)
【答案】②③④
【解析】①因为 平面 ,所以 与平面 不平行,故①错误;格致课堂
②连接 ,易证 .
因为 ,所以 平面 ,故②正确;
③因为 底面 ,所以 是 与底面 所成的角,所以 ,
故③正确;
④ 与 既无交点也不平行,所以 与 为异面直线,故④正确.
故答案为:②③④.
11.如图,正方形 的边长为2, 与 的交点为 , 平面 , ,且
.
(1)求证: 平面 ;
(2)求直线 与平面 所成角的正切值.
【答案】(1)证明见解析;(2)
【解析】(1)∵ 平面 , 平面
∴ ,又 , ,
, 平面 ,∴ 平面 .
又 平面 ,∴ .格致课堂
∵四边形 是正方形,∴ .
又 , 平面
所以 平面 .
(2)取 的中点 ,连接 , .
∵ 平面 , 平面 ,
∴ ,又 ,∴ .
∵ ,∴ 平面 ,
∴ 为直线 与平面 所成的角
在 中,知 , ,
∴ .
素养达成
12.如图,直三棱柱ABC−ABC 中(侧棱与底面垂直的棱柱),AC=BC=1,∠ACB=90°,AA= ,D
1 1 1 1
是AB 的中点.
1 1
(1)求证:C D⊥平面AABB;
1 1 1
(2)当点F 在BB 上的什么位置时,AB⊥平面C DF ?并证明你的结论.
1 1 1
【答案】(1)见解析;(2)见解析
【解析】(1)∵ 是直三棱柱,
∴AC =BC =1,且∠AC B=90°.
1 1 1 1 1 1 1格致课堂
又D是AB 的中点,
1 1
∴C D⊥AB.
1 1 1
∵AA⊥平面ABC ,C D 平面ABC ,
1 1 1 1 1 1 1 1
∴AA⊥C D,
1 1
∴C D⊥平面 .
1
(2)作 交AB 于点E,延长DE交BB 于点F,连接C F,则AB⊥平面C DF,点F即所求.
1 1 1 1 1
事实上,∵C D⊥平面AABB,AB 平面AABB,
1 1 1 1 1 1
∴C D⊥AB.
1 1
又AB⊥DF, ,
1
∴AB⊥平面C DF.
1 1
∵AA=AB= ,
1 1 1
∴四边形AABB为正方形.
1 1
又D为AB 的中点,DF⊥AB,
1 1 1
∴F为BB 的中点,
1
∴当点F为BB 的中点时,AB⊥平面C DF.
1 1 1