文档内容
2024-2025 学年第一学期期末考试
盐田高级中学高一数学试题卷
命题人:李会玲 审题人:俞兴保 考试时间:120分钟 满分:150分
一、单选题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合要求的.
{ } 1
1.已知集合A= x∈Z x2 ≤4 ,B=x∈R ≤2x <2,则AB=( )
4
A.{ 0,1,2 } B.{−2,−1,0 } C.{−2,−1,0,1 } D.{−1,0,1,2 }
2.对于实数a,b,c,下列命题正确的是( )
A.若a>b,则ac2 >bc2 B.若a>b,则a2 >b2
b c
C.若a>b,则a|a|>b|b| D.若a>b>c>0,则 <
a−b a−c
f(x )− f(x )
3.下列函数,在其定义域内既满足 f(−x)=−f(x)又满足 1 2 >0的是( )
x −x
1 2
1
A. f(x)=3x B. f(x)=log x C. f(x)= x− D. f(x)= x3
3
x
4.已知a=(sin1)−0.1,b=3−sin1,c=log (sin1),则a、b、c的大小关系为( )
2
A.c0)的角的集合是αα= +2kπ,k∈Z;
4
B.扇形的圆心角为0.5弧度,周长为15,则它的面积为9;
π
C.将表的分针拨慢10分钟,则分针转过的角的弧度数是 ;
3
α
D.若α是第三象限角,则 是第二象限角.
2
1 4
6.已知正实数a、b满足a+b=2,则 + 的最小值为( )
a b+1
A.2 B.3 C.2 2 D.3 3
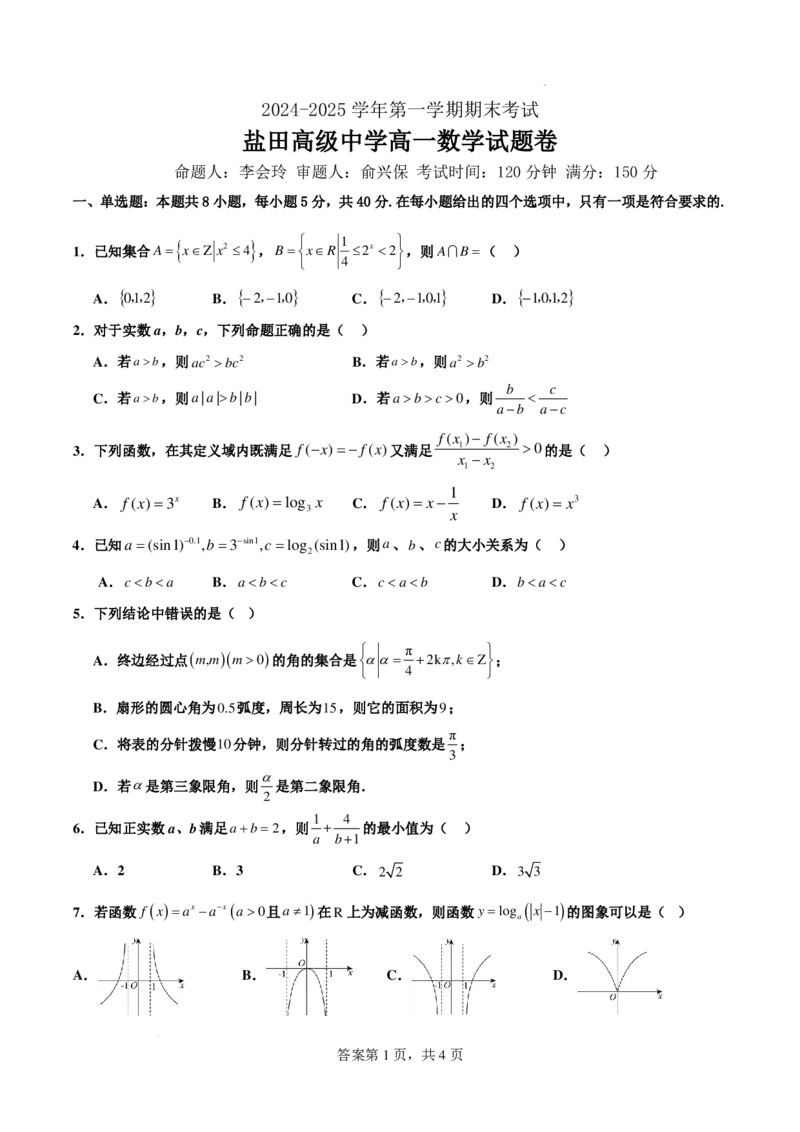
7.若函数 f (x)=ax−a−x (a>0且a≠1)在R上为减函数,则函数y=log ( x −1 ) 的图象可以是( )
a
A. B. C. D.
答案第1页,共4页
学科网(北京)股份有限公司8.已知函数 f (x)=ln ( x2−ax−a−1 ) ,下列说法正确的有( )
A.存在实数a,使 f (x)的定义域为R
B.若函数 f (x)在区间(2,+∞)上单调递增,则实数a的取值范围是(−∞,1)
C.对任意正实数a, f (x)的值域为R
D.函数 f (x)一定有最小值
二、多选题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.全部选
对的得6分,部分选对的得部分分值.
9.下列说法正确的是( )
A.命题“∃x ∈R,x2+3x +2≤0”的否定是“∀x∈R,x2+3x+2>0”
0 0 0
B.a<4是a<3的必要不充分条件
C.函数 f(x)=log (x2 +2x−3)的单调递减区间为(−∞,−1)
3
D.函数 f (x)=ax−1−2(a>0且a≠1)的图象恒过定点1,1 .
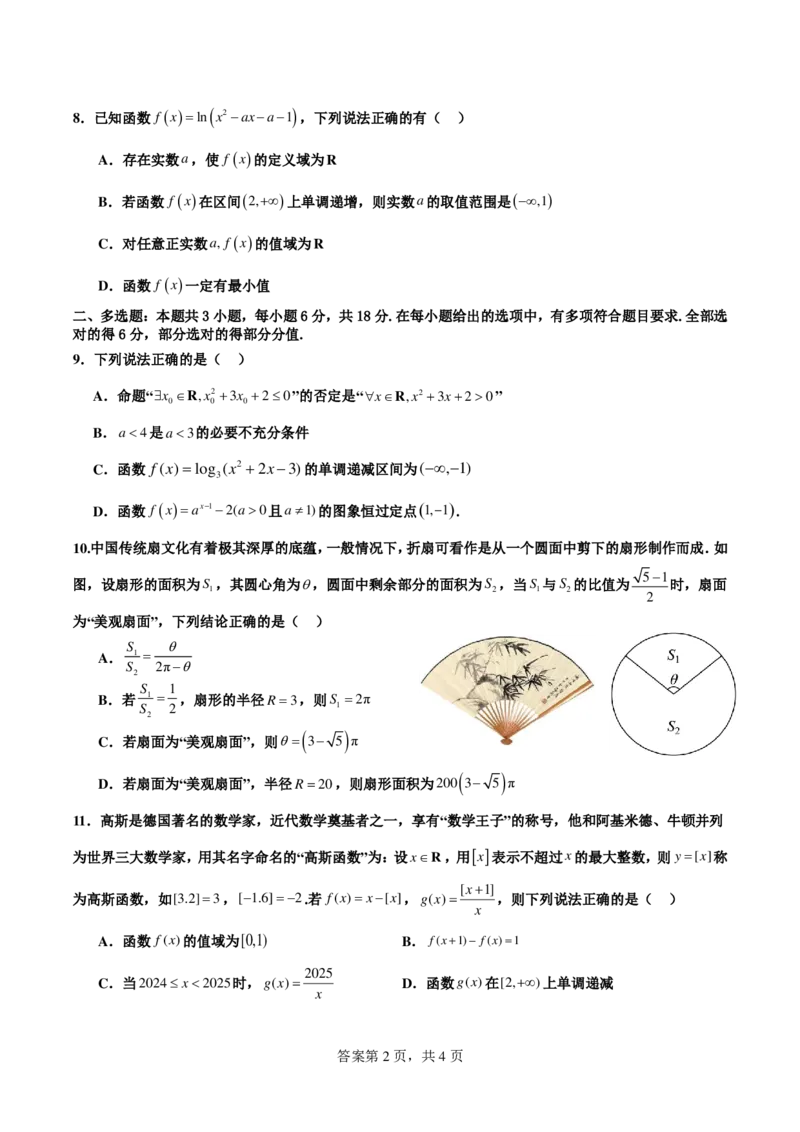
10.中国传统扇文化有着极其深厚的底蕴,一般情况下,折扇可看作是从一个圆面中剪下的扇形制作而成.如
5−1
图,设扇形的面积为S ,其圆心角为θ,圆面中剩余部分的面积为S ,当S 与S 的比值为 时,扇面
1 2 1 2
2
为“美观扇面”,下列结论正确的是( )
S θ
A. 1 =
S 2π−θ
2
S 1
B.若 1 = ,扇形的半径R=3,则S =2π
S 2 1
2
( )
C.若扇面为“美观扇面”,则θ= 3− 5 π
( )
D.若扇面为“美观扇面”,半径R=20,则扇形面积为200 3− 5 π
11.高斯是德国著名的数学家,近代数学奠基者之一,享有“数学王子”的称号,他和阿基米德、牛顿并列
为世界三大数学家,用其名字命名的“高斯函数”为:设x∈R,用[
x
]表示不超过x的最大整数,则y=[x]称
[x+1]
为高斯函数,如[3.2]=3,[−1.6]=−2.若 f(x)=x−[x],g(x)= ,则下列说法正确的是( )
x
A.函数 f(x)的值域为[0,1) B. f(x+1)− f(x)=1
2025
C.当2024≤x<2025时,g(x)= D.函数g(x)在[2,+∞)上单调递减
x
答案第2页,共4页三、填空题:本题共3小题,每小题5分,共15分.
2
12.计算: 2 1
0
+ 3 3
−
3 − 1
1−log32
⋅log 9⋅log 4= .
3 8 3 4 27
4 π
13.已知sinθ+cosθ= ,θ∈0, ,则sinθ−cosθ的值为 .
3 4
3x+1,x≤0
14.设函数 f (x)= ,若关于x的函数g(x)= [ f(x) ]2 −(a+2)f(x)+a+1恰好有五个零点,
log
4
x,x>0
则实数a的取值范围是 .
四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.
15.(本小题满分13分)设全集U =R,已知集合A= x| x+1 ≤0 ,集合B= { x|x2+3x−10<0 } ,
x−4
(1)求A∩B和C (A∪B);
U
{ }
(2)若C = xa≤ x≤2a+2 且A∩C =C,求实数a的取值范围.
3
16.(本小题满分15分)已知角α以x轴的非负半轴为始边,点P(4,−3m)在角α的终边上,且sinα= ,
5
(1)求m及tanα的值;
π
2sin(π−α)+sin(α+ )tan(π−α)
2
(2)求 的值.
3π π
sin( −α)+cos( +α)
2 2
17.(本小题满分15分)已知幂函数 f (x)= ( m2+m−5 ) ⋅xm(m∈R )是定义在R上的偶函数.
(1)求函数 f (x)的解析式;
1
(2)当x∈ 3 ,81 时,求函数g(x)= f (log 3 x)−2log 3 f (x) +2的最大值,并求对应的自变量x的值.
答案第3页,共4页
学科网(北京)股份有限公司18.(本小题满分17分)已知函数 f(x)=ax2 −(a+1)x+1(a∈R).
(1)若 f (x)在区间(−∞,1 ]上单调递减,求a的取值范围.
(2)求关于x的不等式 f (x)>0的解集.
19.(本小题满分17分)已知偶函数 f (x)和奇函数g(x)的定义域均为R,且 f(x)−g(x)=21−x.
(1)求函数 f (x)和g(x)的解析式;
(2)若∀x∈R,不等式mf(x)≤ [ g(x) ]2 +2m+4恒成立,求实数m的取值范围;
f(x)+g(x) 2 g(x)− f(x) 2
(3)若h(x)= + −2mg(x),且h(x)在[1,+∞)上的最小值为−2,求m的值.
2 2
答案第4页,共4页2024-2025 学年第一学期期末考试
盐田高级中学高一数学试题卷参考答案:
题号 1 2 3 4 5 6 7 8 9 10
答案 B C D A D B A C ABD ACD
题号 11
答案 AC
12.1
2
【解析】 2 1
0
+ 3 3
−
3 − 1
1−log32
⋅log 9⋅log 4
3 8 3 4 27
2
=1+
3
3
− 3
−3log32−1⋅
lg32
⋅
lg22
=1+
3
−2
−
3log32
⋅
2lg3
⋅
2lg2
=1+
4
−
2
×
2
=1.故答案为:1.
2 lg22 lg33 2 3 2lg2 3lg3 9 3 3
2
13.−
3
4 π 16
【解析】由sinθ+cosθ= ,θ∈(0, ),可得1>cosθ>sinθ>0,1+2sinθcosθ= ,
3 4 9
7 2
∴2sinθcosθ= .∴sinθ−cosθ=− (sinθ−cosθ)2 =− 1−2sinθcosθ=− .
9 3
2
故答案为:− .
3
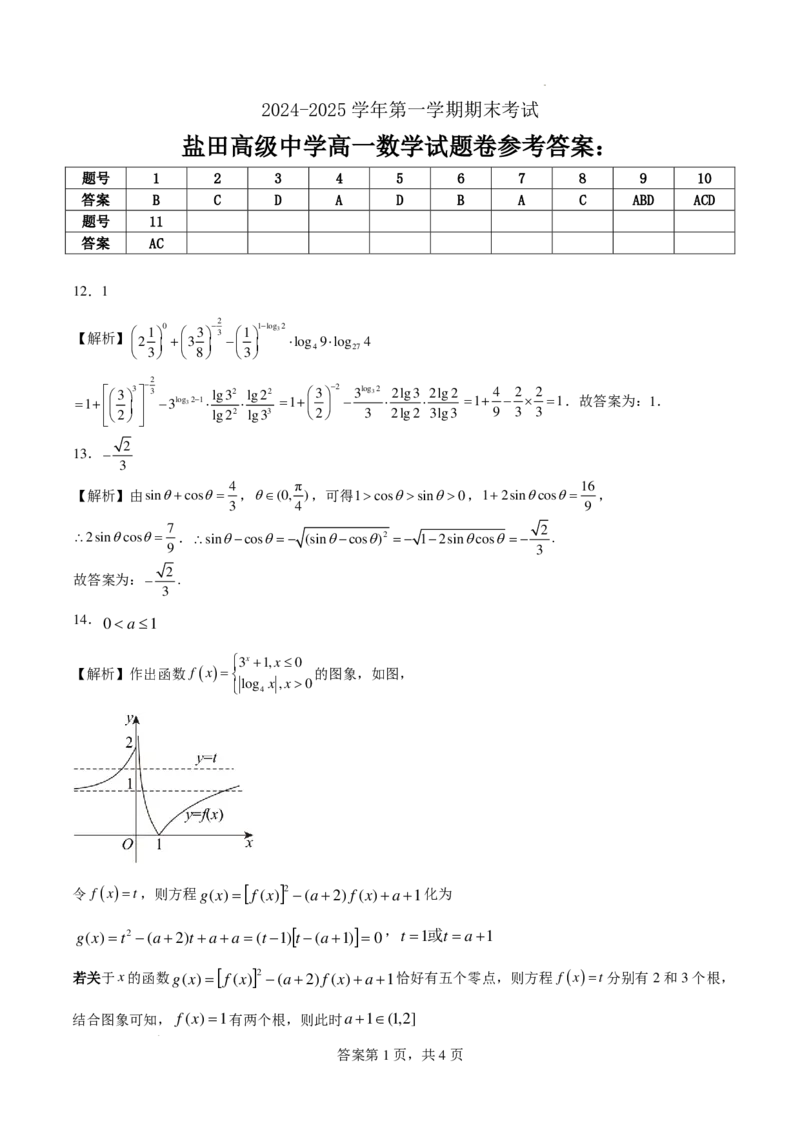
14. 00
令 f (x)=t,则方程g(x)= [ f(x) ]2 −(a+2)f(x)+a+1化为
g(x)=t2 −(a+2)t+a+a=(t−1) [ t−(a+1) ] =0 , t =1或t =a+1
若关于x的函数g(x)= [ f(x) ]2 −(a+2)f(x)+a+1恰好有五个零点,则方程 f (x)=t分别有2和3个根,
结合图象可知, f(x)=1有两个根,则此时a+1∈(1,2]
答案第1页,共4页
学科网(北京)股份有限公司12a+2,解得a<−2,满足题意;
a≥−1
当C ≠∅时,则a≥−2,且 ,解得−1≤a<1,则−1≤a<1;
2a+2<4
综上,实数a的取值范围为(−∞,−2)[−1,1).
3
16.(1)m=−1;tanα= ;(2)
4
3
【解析】(1)因为点p(4,−3m)角α的终边上,且sinα= ,
5
−3m 3
根据三角函数定义sinα= = >0,则m<0,
16+9m2 5
解得m=−1或m=1(舍),
y 3
所以tanα= = .
x 4
π
2sin(π−α)+sin(α+ )tan(π−α)
2sinα+cosα(−tanα) sinα
2
则 = =
3π π −cosα−sinα −cosα−sinα
sin( −α)+cos( +α)
2 2
3
tanα 3
4
= = =− ,
−1−tanα 3 7
−1−
4
1
17.(1) f (x)=x2 (2)当x= 时,函数g(x)的最大值为7
3
【解析】(1)根据题意可得m2+m−5=1,即m2+m−6=0,
所以(m+3)(m−2)=0,解得m=−3或m=2,又函数 f (x)是定义在R上的偶函数,
答案第2页,共4页
学科网(北京)股份有限公司所以m=2, f (x)=x2,即函数 f (x)的解析式为 f (x)=x2.
(2)由(1)可知g(x)= f (log x)−2log f (x) +2
3 3
=(log x)2−2log x2+2=(log x)2−4log x+2 =(log x−2)2−2
3 3 3 3 3
1 1
因x∈
3
,81
,所以log
3
x∈[−1,4],当x=
3
时,log
3
x=−1,函数g(x)的最大值为7.
18.(1)0≤a≤1(2)答案见详解.
【解析】(1)当a=0时, f (x)=−x+b的单调递减区间为R,满足题意;
−(a+1)
− ≥1
当a≠0时,由 f (x)在(−∞,1 ]上单调递减可得 2a ,解得00
综上,0≤a≤1.
(2) f (x)>0⇔ax2−(a+1)x+1>0⇔(ax−1)(x−1)>0,
1)当a=0时,由−(x−1)>0解得x<1;
1
2)当a≠0时,方程(ax−1)(x−1)=0的两根为 ,1,
a
1 1
当a<0时, <1,解不等式(ax−1)(x−1)>0得 1,解不等式(ax−1)(x−1)>0得x<1或x> ;
a a
1 1
当a>1时, <1,解不等式(ax−1)(x−1)>0得x>1或x< ;
a a
当a=1时,由(x−1)2 >0得x≠1.
综上,当a=0时,不等式解集为(−∞,1);
1
当a<0时,不等式解集为 ,1;
a
1
当01时,不等式解集为−∞, (1,+∞);
a
当a=1时,不等式解集为(−∞,1)(1,+∞)
.
19.(1) f(x)=2x +2−x,g(x)=2x −2−x(2)m≤8(3)∴m=2
【解析】(1)由题, f (x)−g(x)=21−x,
答案第3页,共4页
学科网(北京)股份有限公司则有 f (−x)−g(−x)=21+x,
又因为偶函数 f (x)和奇函数g(x),所以 f (x)+g(x)=21+x,
f (x)−g(x)=21−x
所以联立 ,解得 f(x)=2x +2−x,g(x)=2x −2−x.
f (x)+g(x)=21+x
(2)因为 f(x)=2x +2−x,g(x)=2x −2−x,
由mf(x)≤[g(x)]2 +2m+4,
可得m(2x +2−x)≤(2x −2−x)2 +2m+4,即m(2x +2−x)≤(2x +2−x)2 +2m
令t=2x+2−x,因为 2x+2−x ≥2 2x⋅2−x =2 ,当且仅当2x =2−x,即x=0时等号成立,
所以t =2x+2−x ≥2所以mt ≤t2 +2m 恒成立,其中t ≥2,
当x=0时,t =2,则2m≤4+2m,m∈R
t2
当x≠0时,m≤ 在t∈[2,+∞)恒成立
t−2
t2 t2 −4+4 (t−2)(t+2)+4 4 4
y = = = =t+2+ =t−2+ +4
t−2 t−2 t−2 t−2 t−2
令
4
≥2 4+4=8,当且仅当t−2= ,即t =4时等号成立
t−2
∴m≤8
f(x)+g(x) 2 g(x)− f(x) 2
(3)h(x)= + −2mg(x)=22x +2−2x −2m(2x −2−x)
2 2
1 3
令t =2x则u =t− (t ≥ ),易知u(t)单调递增,
t 2
3
∴h=t2 +2−2mt =t2 −2mt+2(t ≥ )的最小值为−2
2
3 3 9 3 25
当m< 时,t = 使函数取得最小值,即 −2m +2=−2,∴m= 不成立
2 2 4 2 12
3
当m≥ 时,t =m使函数取得最小值,即m2 −2m2 +2=−2,∴m=(2 符合),m=−2不成立
2
综上:∴m=2
答案第4页,共4页
学科网(北京)股份有限公司