数学-四川省绵阳市南山中学2023-2024学年高一下学期期末统考_2024-2025高一（7-7月题库）_2024年7月试卷_0701四川省绵阳市南山中学2023-2024学年高一下学期期末统考

秘密 ★ 启用前 【考试时间：2024年6月24日上午8:20-10:20】 绵阳南⼭中学2024年春季⾼2023级期末热身试题 数 学 注意事项： 1．答题前，考⽣务必将⾃⼰的班级、姓名⽤0.5毫⽶⿊⾊签字笔填写清楚，同时⽤2B铅笔将准考证 号准确填涂在“考号”栏⽬内. 2．选择题使⽤2B铅笔填涂在答题卡对应题⽬标号的位置上，如需改动，⽤橡⽪擦擦⼲净后再选涂 其它答案；⾮选择题⽤0.5毫⽶⿊⾊签字笔书写在答题卡的对应框内，超出答题区域书写的答案 ⽆效；在草稿纸、试题卷上答题⽆效． 3．考试结束后，将答题卡交回． 一.选择题：本题共8小题，每小题5分，共40分. 在每小题给出的四个选项中，只有一个是符合题目要求 的. 1. 已知复数z满⾜(1−i)z = 1+i，则复数z的虚部为 A.1 B.−1 C.i D.−i 2 2 2. cos15∘− sin15∘ = 2 2 3 1 1 3 A. B. C.− D.− 2 2 2 2 3. 已知等边三⾓形ABC的边长为1，设BC = a,⃗ CA = b, ⃗ AB = c，⃗ 则a ⃗⋅ b ⃗ + b ⃗ ⋅ c ⃗+ c ⃗⋅ a ⃗= 3 3 A.3 B.−3 C. D.− 2 2 1 4. 已知⾓α与β的终边关于y轴对称，cosβ = − ，则tanα = 2 3 3 A. 3 B. C.± D.± 3 3 3 5. 已知m,n,l表⽰直线，α,β表⽰平⾯，则下列命题正确的是 A.α ⊥ β,α ∩β = l,m ⊥ l，则m ⊥ β B.m ⊂ α,n ⊂ β,α ⊥ β，则m ⊥ n C.m ⊂ α,m ⊥ β，则α ⊥ β D.m//α,n ⊂ α，则m//n 第 1 页 {#{QQABBQQEggAIQIAAAQhCUwUCCAKQkACCAQgOgAAEoAAAwBFABCA=}#}6. 已知ΔABC中，点D,E满⾜BD = 2DC，AE = 4ED，则BE = 11 8 2 8 11 8 2 8 A. AB− AC B. AB− AC C.− AB+ AC D.− AB+ AC 15 15 3 15 15 15 3 15 7. 已知直线y = a(a ∈ R)与函数y = 2sin2x和y = 2sin(2x +φ)的图像分别交于点F,G，若F在G的左 π 边，且|FG| = ，则φ = min 6 π π π 2π A. B. C.− D. 6 3 3 3 8. 三⾓形ABC中，点O是ΔABC的外⼼，AB = 6，AC = 8，则OA⋅BC = A.14 B.−14 C.−28 D.28 二.选择题：本题共3小题，每小题6分，共18分. 在每小题给出的四个选项中，有多项符合题目要求，全 部选对得6分，少选得部分分，有错选得0分. 9. 已知函数f(x) = 3sin2x +cos2x +1，则 π A.f(x)的最⼩正周期是π B.f(x)的图像关于点(− ,0)中⼼对称 12 π π 3π C.f(x + )是偶函数 D.f(x)在区间[− , ]上恰有4个零点 12 6 2 10.在三⾓形ABC中，内⾓A,B,C所对的边分别为a,b,c，则 A.若A > B，则sin A > sinB B.若sin2A = sin2B，则ΔABC是等腰三⾓形 π C.若a = 2 3,b = 4,A = ，则满⾜条件的三⾓形有两个 4 AB AC AB AC 1 D.若( + )⋅BC = 0，且 ⋅ = ，则ΔABC是等边三⾓形 2 |AB| |AC| |AB| |AC| 11.如图，三棱锥P −ABC中，ΔABC为边长是 3的正三⾓形，PA ⊥ 底⾯ABC，PA = 2，点Q是线段 BC上⼀动点，则下列说法正确的是 3 A.点B到平⾯PAQ的距离的最⼤值为 2 B.三棱锥P −ABC的外接球表⾯积为8π π C.直线PB与AQ所成⾓可能是 4 4 D.直线AQ与平⾯PBC所成⾓的正切值的最⼤值为 3 第 2 页 {#{QQABBQQEggAIQIAAAQhCUwUCCAKQkACCAQgOgAAEoAAAwBFABCA=}#}三.填空题：本题共3个小题，每小题5分，共15分. 把答案直接填在答题卷中的横线上. 12.⼀个圆台的上、下底⾯的半径分别为1和4，体积为28π，则此圆台的表⾯积为_____. π 1 2π 13.已知sin( −α) = ，则cos( +2α) = _____. 6 3 3 14.已知函数f(x) = λsin(ωx +φ)(λ > 0,ω > 0,0 < φ < π)部分图象如图1所⽰，点A,B分别为图象的最 ⾼点和最低点，过A,B作x轴的垂线，分别交x轴于点A′, B′， 点C为该部分图象与x轴的交点，f(x)与y 3 π 轴的交点为D(0, )，此时A′ B′ = B′ B.将绘有该图象的纸⽚沿x轴折成 的⼆⾯⾓α −OC−β，如 2 3 图2所⽰，折叠后|AB| = 2，在图2中，若P ,P 是f(x)上两个不同的点，且满⾜ 1 2 AP ⊥ BB′, AP ⊥ BB′， 则|P P |的最⼩值为____. 1 2 1 2 四.解答题：共77分. 解答应写出文字说明、证明过程或演算步骤. 15.(本题满分13分) 已知向量OA = (2,1)，OB = (3,−2)，OC = (6−m,−3−m). (1)若点A,B,C不能构成三⾓形，求实数m的值； (2)若ΔABC为直⾓三⾓形，求实数m的值. 16.(本题满分15分)某居民⼩区为缓解业主停车难的问题，拟对⼩区内⼀块扇形空地AOB进⾏改建．如 图所⽰，⽅案⼀:平⾏四边形OMPN区域为停车场，⽅案⼆:矩形MPQH区域为停车场，其余部分建 成绿地.点P在围墙弧AB上，点M在道路OA上，点N,Q,H在道路OB上， π 且OA = R⽶，∠AOB = ，设∠POB = α． 3 (1)当点P为弧AB的中点时，求OM⋅ON的值； (2)记平⾏四边形OMPN的⾯积为S ，矩形MPQH的⾯积为S ，说明S ，S 1 2 1 2 的⼤⼩关系，并求α为何值时，停车场⾯积最⼤？最⼤值是多少？ 第 3 页 {#{QQABBQQEggAIQIAAAQhCUwUCCAKQkACCAQgOgAAEoAAAwBFABCA=}#}17.(本题满分15分) 如图，在四棱锥P −ABCD中，底⾯ABCD为正⽅形，PA ⊥ 底⾯ABCD，PA = AB，E,M分别为 棱PB,CD的中点，F为棱BC上的动点． (1)证明：EM//平⾯PAD； (2)试问平⾯AEF与平⾯PBC是否互相垂直？如果垂直，请证明；如果 不垂直，请说明理由． 18.(本题满分17分) 如图，在ΔABC中，已知AB = 2，AC = 5，(sin A+sinB)(sin A−sinB) = sin2C−sinBsinC， BC边上的中点为M，点N是边AC上的动点(不含端点)，AM，BN相交于点P. (1)求边BC的长； (2)当点N为AC中点时，求∠MPN的余弦值； (3)设BP = λBN，求NA⋅NB的最⼩值； 当NA⋅NB取得最⼩值时，求λ的值. 19.(本题满分17分) 刻画空间的弯曲性是⼏何研究的重要内容，⽤曲率刻画空间的弯曲性，规定：多⾯体顶点的曲率等 于2π与多⾯体在该点的⾯⾓之和的差，其中多⾯体的⾯的内⾓叫做多⾯体的⾯⾓，⾓度⽤弧度制． π π 例如:正四⾯体每个顶点均有3个⾯⾓，每个⾯⾓均为 ，故其各个顶点的曲率均为2π −3× = π． 3 3 2π 如图，在直三棱柱ABC−A B C 中，点A的曲率为 ，N,M分别为AB,CC 的中点，且AB = AC. 1 1 1 1 3 (1)证明：CN ⊥ 平⾯ABB A ; 1 1 (2)证明：平⾯AMB ⊥ 平⾯ABB A ; 1 1 1 (3)若AA = 2AB，求⼆⾯⾓A−MB −C 的正切值. 1 1 1 第 4 页 {#{QQABBQQEggAIQIAAAQhCUwUCCAKQkACCAQgOgAAEoAAAwBFABCA=}#}绵阳南山中学 2024 年春季高 2023 级热身考试 数学试题参考答案及评分标准 一、选择题 题 号 1 2 3 4 5 6 7 8 9 10 11 选 项 A B D D C D C B AD ACD ABD 三、填空题（每个小题 5分，共 15 分） 7 2 12. 42 13.  14. 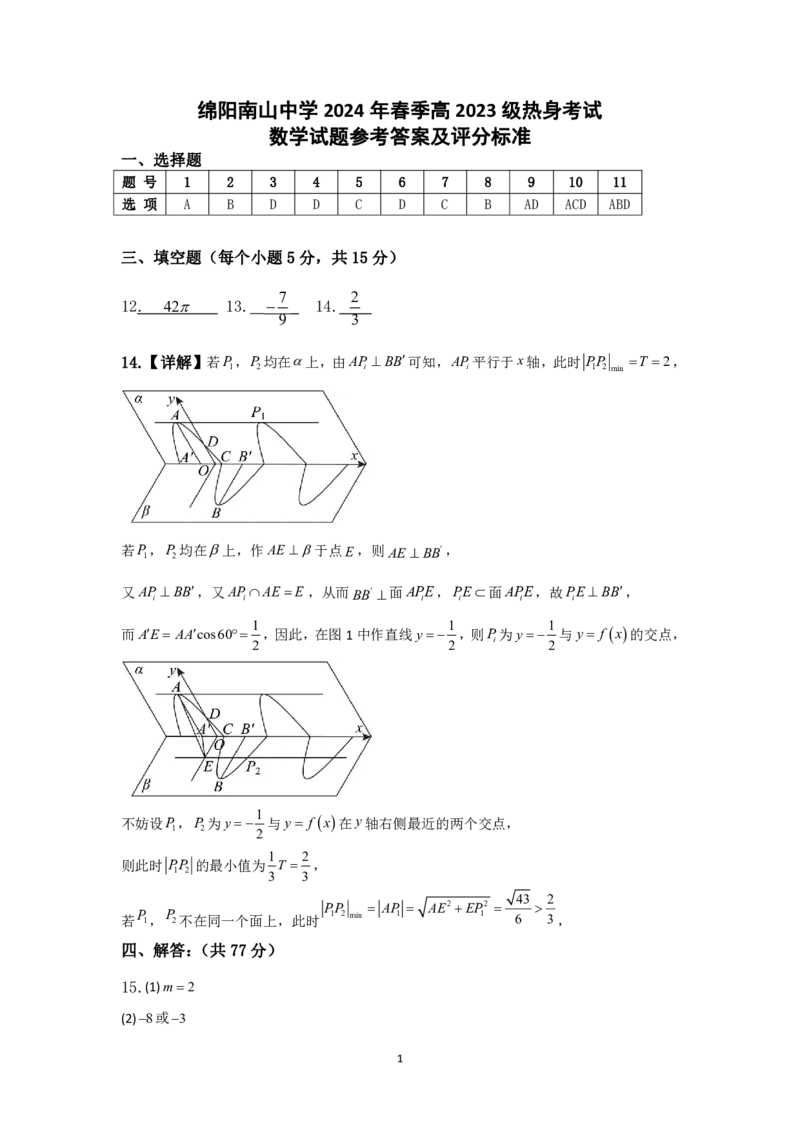9 3 14.【详解】若P，P均在上，由AP BB可知，AP平行于x轴，此时 PP T 2， 1 2 i i 1 2 min 若P，P均在上，作AE 于点E，则AE BB， 1 2 又AP BB，又APAE E ，从而BB 面APE，PE面APE，故PEBB， i i i i i i 1 1 1 而AE AAcos60 ，因此，在图1中作直线y ，则P为y 与y f x的交点， 2 2 i 2 1 不妨设P，P为y 与y f x在y轴右侧最近的两个交点， 1 2 2 1 2 则此时 PP 的最小值为 T  ， 1 2 3 3 43 2 PP  AP  AE2EP2   若 P 1， P 2不在同一个面上，此时 1 2 min 1 1 6 3， 四、解答：（共 77分） 15.(1)m2 (2)8或3 1 {#{QQABBQQEggAIQIAAAQhCUwUCCAKQkACCAQgOgAAEoAAAwBFABCA=}#}  【分析】（1）当三点共线时，点A，B，C不能构成三角形，即AB,AC共线，利用向量共线 的坐标公式计算即可得出答案. （2）ABC为直角三角形，分A为直角，B为直角和C为直角，利用垂直向量的坐 标表示即可得出答案.   【详解】（1）因为点A，B，C不能构成三角形，所以AB∥AC ，..........2分    因为OA2,1，OB3,2，OC6m,3m，    所以ABOBOA3,22,11,3，    ACOCOA6m,3m2,14m,4m，   AB∥AC，所以14m34m，解得m2， 综上可得，当m2时，A，B，C不能构成三角形；..........6分   （2）①若A为直角，则ABAC，所以ABAC14m34m0， 解得m8；..........8分    ②若B为直角，则ABBC，BCOCOB6m,3m3,23m,1m   所以ABBC13m31m0，解得m3；..........10分 ③若C为直角，则BC  AC，   所以BCAC3m4m1m4m0， 即m2m80，因为1248310 ，所以方程无解；..........12分 综上可得，当m8或m3时ABC为直角三角形...........13分 R2 16.(1) 6 π 3R2 (2)S =S ，当 ，最大为 m2． 1 2 6 6 【分析】（1）根据P点位置，利用正弦定理得到OM ,ON的长度，利用数量积公式可得. （2）由面积公式可知S =S ，求S ，S 都可以利用正弦定理得到边的长度，再根据面积公 1 2 1 2 式，结合三角函数可得最大值. π 【详解】（1）当点P为弧AB的中点时， ， 6 2 {#{QQABBQQEggAIQIAAAQhCUwUCCAKQkACCAQgOgAAEoAAAwBFABCA=}#}2  在△PON中，PNO ，∴OPN  ，∴ON PN OM 3 6 OP ON 3 由正弦定理  得ON  R sinONP sinOPN 3    R2 ∴OM ON ON2cos  ...........5分 3 6 （2）因为矩形与平行四边形的底和高都相等，所以S =S ...........7分 1 2 若由平行四边形计算停车场面积 2  由平行四边形OMPN 得，在OPN中，ONP ，OPN  ， 3 3 ON R NP ON OP NP   则   ，即   2 sin， sinOPN sinONP sin sin  sin 3  3 2 3   3 即ON  Rsin Rcos sin， 3 3  3 2 3 NP Rsin 3 则停车场面积 2 3  3  2 S  NPNOsinONP RsinRcos Rsinsin 1 3   3   3  3  1 31cos2  R2sincos sin2 R2 sin2       3  2 3 2  3R2  ( 3sin2cos1) 6 3R2    π  2sin2 1 ，其中0 6   6  3 π π 5π 所以 2  ， 6 6 6 π π π 3R2 则2  时，即 时，S  6 2 6 max 6 若由矩形计算停车场面积 在Rt△OQP中，QP Rsin，OQRcos， 3 3 在RtVOHM 中，OH  Rsin，∴HQRcos Rsin 3 3 则停车场面积  3  S  HQPQ RsinRcos Rsin 2   3   3 {#{QQABBQQEggAIQIAAAQhCUwUCCAKQkACCAQgOgAAEoAAAwBFABCA=}#} 3  1 31cos2  R2sincos sin2 R2 sin2       3  2 3 2  3R2  ( 3sin2cos1) 6 3R2    π  2sin2 1 ，其中0 ． 6   6  3 π π 5π 所以 2  ， 6 6 6 π π π 3R2 则2  时，即 时，S  6 2 6 max 6 π 3R2 答：不管是方案一还是方案二，当 时，停车场面积最大，最大为 m2．........15分 6 6 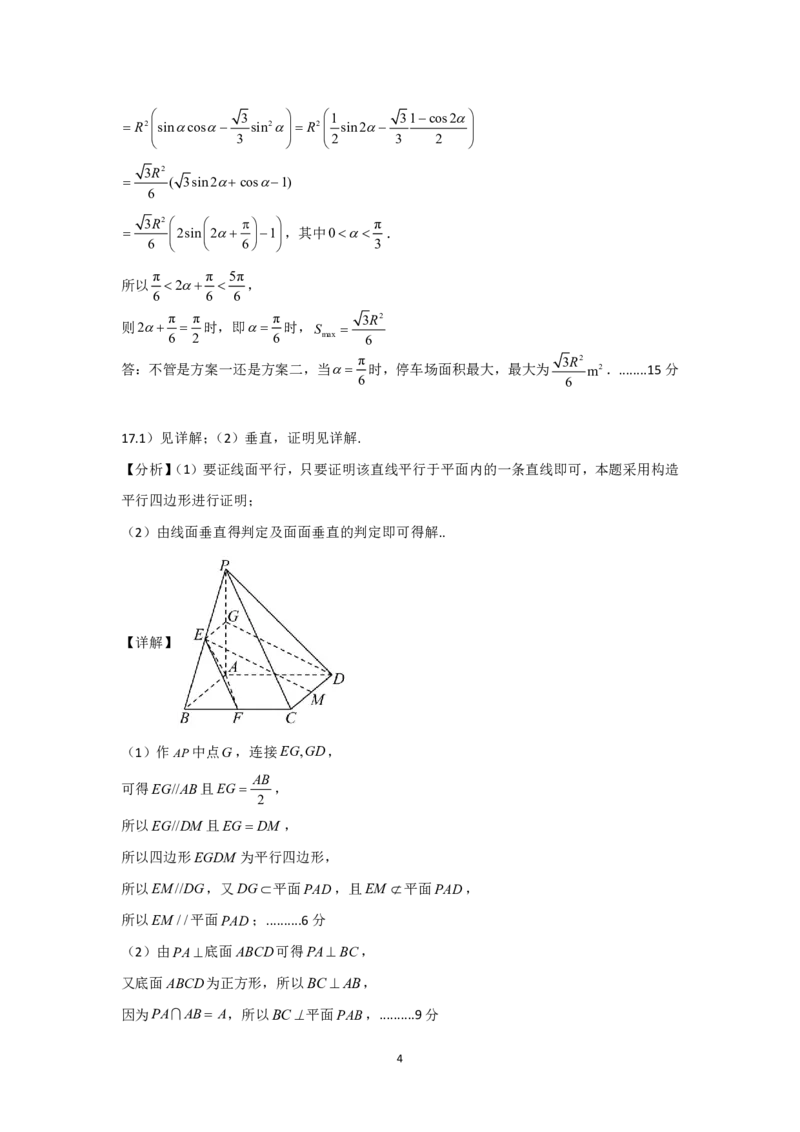17.1）见详解；（2）垂直，证明见详解. 【分析】（1）要证线面平行，只要证明该直线平行于平面内的一条直线即可，本题采用构造 平行四边形进行证明； （2）由线面垂直得判定及面面垂直的判定即可得解.. 【详解】 （1）作AP中点G，连接EG,GD， AB 可得EG//AB且EG ， 2 所以EG//DM且EGDM ， 所以四边形EGDM 为平行四边形， 所以EM//DG，又DG平面PAD，且EM 平面PAD， 所以EM //平面PAD；..........6分 （2）由PA底面ABCD可得PABC， 又底面ABCD为正方形，所以BCAB， 因为PAAB A，所以BC平面PAB，..........9分 4 {#{QQABBQQEggAIQIAAAQhCUwUCCAKQkACCAQgOgAAEoAAAwBFABCA=}#}又BC平面PBC，所以平面PBC平面PAB， 根据PA AB，E为棱PB中点，所以AE PB， 因为平面PBC平面PAB PB，所以AE 平面PBC，..........12分 由AE平面AEF ，所以平面AEF 平面PBC， 所以平面AEF 与平面PBC垂直...........15分 18.(1)BC 19； 4 91 (2) ； 91 1 10 (3) ， . 4 11 【分析】（1）由余弦定理求解即可.      1 1   1 （2）设ABa,ACb，由中点可得AM  a b,BN a b ，再由数量积的运算性质 2 2 2 求解即可.       （3）设 NA  x,则NANBNA(NAAB)可转化为关于x的二次函数，求最值，再由  9  1 BP( BA BM)及三点共线得解即可. 10 5 【详解】（1） sin AsinB  sin AsinB sin2CsinBsinC 得 BAC 60 在ABC中， AB2,AC5,BAC60 ，由余弦定理知： BC2  AB2AC22ABACcosBAC 2252225cos60 19， 所以BC 19...........5分      1 1   1 （2）设ABa,ACb，由M,N分别为BC,AC的中点，得AM  a b,BN a b， 2 2 2     1  1   1 1 而|a|2,|b|5,ab 25 5，则|AM | (ab)2  222525  39 ， 2 2 2 2   1  1 1 |BN | (a b)2  45 25  21 ， 2 4 2   1    1  1  1   1  1 1 又AM BN  (ab)(a b) |a|2  ab |b|22 5 253， 2 2 2 4 4 4 4   AM BN 3 4 91 cosMPN      |AM ||BN | 1 1 91 ， 39 21 2 2 4 91 所以MPN的余弦值为 ...........11分 91 5 {#{QQABBQQEggAIQIAAAQhCUwUCCAKQkACCAQgOgAAEoAAAwBFABCA=}#}（3）设|  N  A  |x，  N  A    N  B    N  A  (  N  A    A  B  )  N  A  2   N  A    A  B   x22x 1 (x 1 )2 1 ， 2 2 4 1  1   1 当x ，即|NA| 时，NANB取最小值 ； 2 2 4  1   9  1      显然AN  AC，则BN  BA BC，而BC2BM,BPBN(01)， 10 10 10  9  1 9  9  因此BP( BA BM) BA BM ，又A,P,M 三点共线，则  1， 10 5 10 5 10 5 10 所以 ...........17分 11 19.(1)证明见解析； (2)证明见解析； 6 (3) ． 3 【分析】（1）由题意可得CN  AB，根据线面垂直的性质可得AA CN ，结合线面垂直的 1 判定定理即可证明； （2）如图，易证DM //CN，由（1）得DM 平面ABBA ，结合面面垂直的判定定理即可 1 1 证明； （3）如图，根据线面垂直的判定定理可得AF 平面BBCC，则AF BM ，易证AH BM ， 1 1 1 1 则∠AHF为二面角AMB C的平面角的补角．结合等面积法求得FH，即可求解. 1 1 【详解】（1）在直三棱柱ABCABC 中，AA 平面ABC，AC,AB平面ABC， 1 1 1 1 π 2π 则AA  AC，AA  AB，所以点A的曲率为2π2 BAC  ， 1 1 2 3 π 所以BAC  ．因为AB AC，所以△ABC为正三角形． 3 因为N为AB的中点，所以CN AB． 又AA 平面ABC，CN 平面ABC，所以AA CN ， 1 1 因为AA AB A，AA、AB 平面ABBA ，所以CN 平面ABBA ．..........4分 1 1 1 1 1 1 （2）取AB的中点D，连接DM，DN． 1 1 因为N为AB的中点，所以DN//BB且DN  BB ． 1 2 1 6 {#{QQABBQQEggAIQIAAAQhCUwUCCAKQkACCAQgOgAAEoAAAwBFABCA=}#}1 又CM //BB 且CM  BB，所以DN //CM 且DN CM ， 1 2 1 所以四边形CNDM为平行四边形，则DM //CN． 由（1）知CN 平面ABBA ，则DM 平面ABBA ． 1 1 1 1 又DM平面AMB ，所以平面AMB 平面ABBA ．..........10分 1 1 1 1 （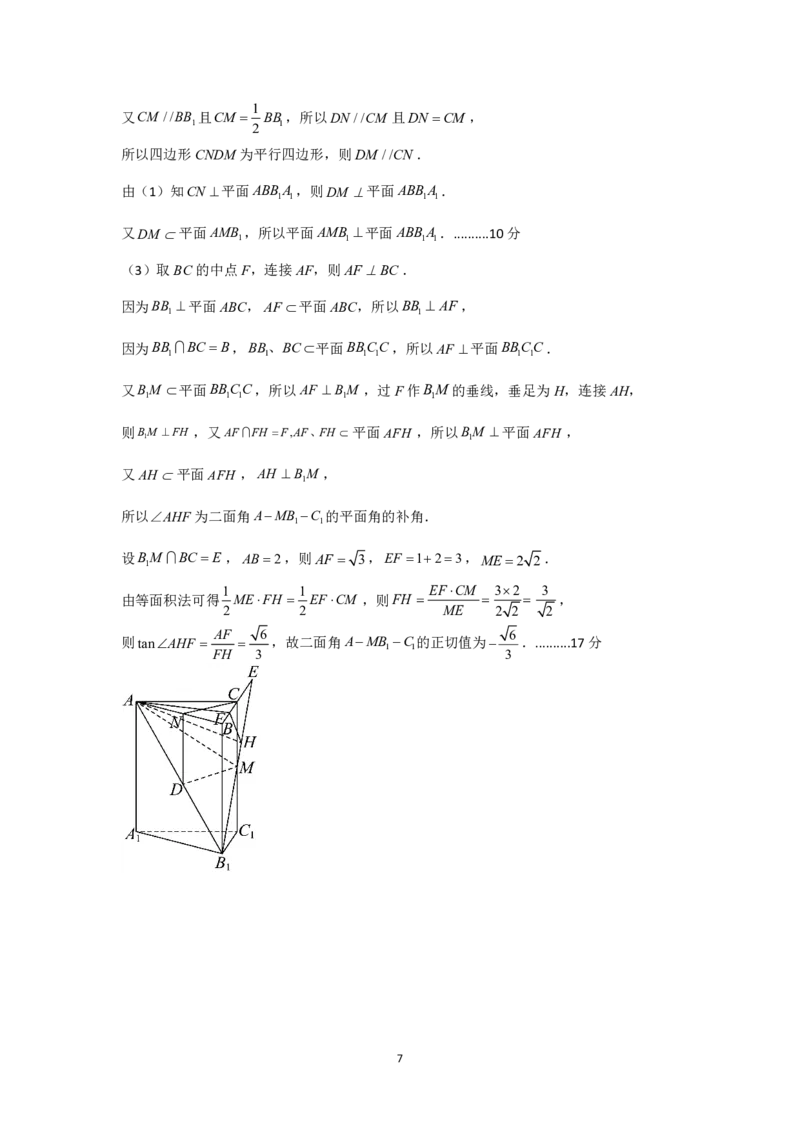3）取BC的中点F，连接AF，则AFBC． 因为BB 平面ABC，AF 平面ABC，所以BB  AF， 1 1 因为BB BCB，BB、BC平面BBCC，所以AF 平面BBCC． 1 1 1 1 1 1 又BM 平面BBCC，所以AF BM ，过F作BM的垂线，垂足为H，连接AH， 1 1 1 1 1 则BM FH ，又AFFH F,AF、FH  平面AFH ，所以BM 平面AFH ， 1 1 又AH平面AFH ，AH BM ， 1 所以∠AHF为二面角AMB C 的平面角的补角． 1 1 设BM BCE，AB2，则AF  3，EF 123，ME2 2． 1 1 1 EFCM 32 3 由等面积法可得 MEFH  EFCM ，则FH    ， 2 2 ME 2 2 2 AF 6 6 则tanAHF   ，故二面角AMB C的正切值为 ．..........17分 1 1 FH 3 3 7 {#{QQABBQQEggAIQIAAAQhCUwUCCAKQkACCAQgOgAAEoAAAwBFABCA=}#}