文档内容
格致课堂
2019-2020学年下学期高一数学第二学期期中模拟测试卷
数学(提高卷)
(考试时间:120分钟 试卷满分:150分)
注意事项:
1.答卷前,考生务必将自己的姓名、考生号等填写在答题卡和试卷指定位置上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑。如需改动,用
橡皮擦干净后,再选涂其他答案标号。回答非选择题时,将答案写在答题卡上。写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
4.测试范围:2019版人教A第二册 第一章 平面向量 第二章 复数
一、单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题
目要求的.
1.若复数(1–i)(a+i)在复平面内对应的点在第二象限,则实数a的取值范围是( )
A.(–∞,1) B.(–∞,–1)
C.(1,+∞) D.(–1,+∞)
2.已知 是虚数单位,给出下列命题,其中正确的是( )
A.满足 的复数 对应的点的轨迹是圆
B.若 , ,则
C.复数 (其中 、 )的虚部为
D.在复平面内,实轴上的点都表示实数,虚轴上的点都表示虚数
3.设非零向量 , 满足 ,则( )
A. B. C. // D.
4.已知 , 的夹角为 ,则以 为邻边的平行四边形的一条对
角线长为 ( )
A.15 B. C.14 D.16格致课堂
5.已知复数 , , ,它们在复平面 上所对应的点分别为A,B,C.
若 ( ),其中 为原点,则 的值是( )
A.1 B.2 C.3 D.4
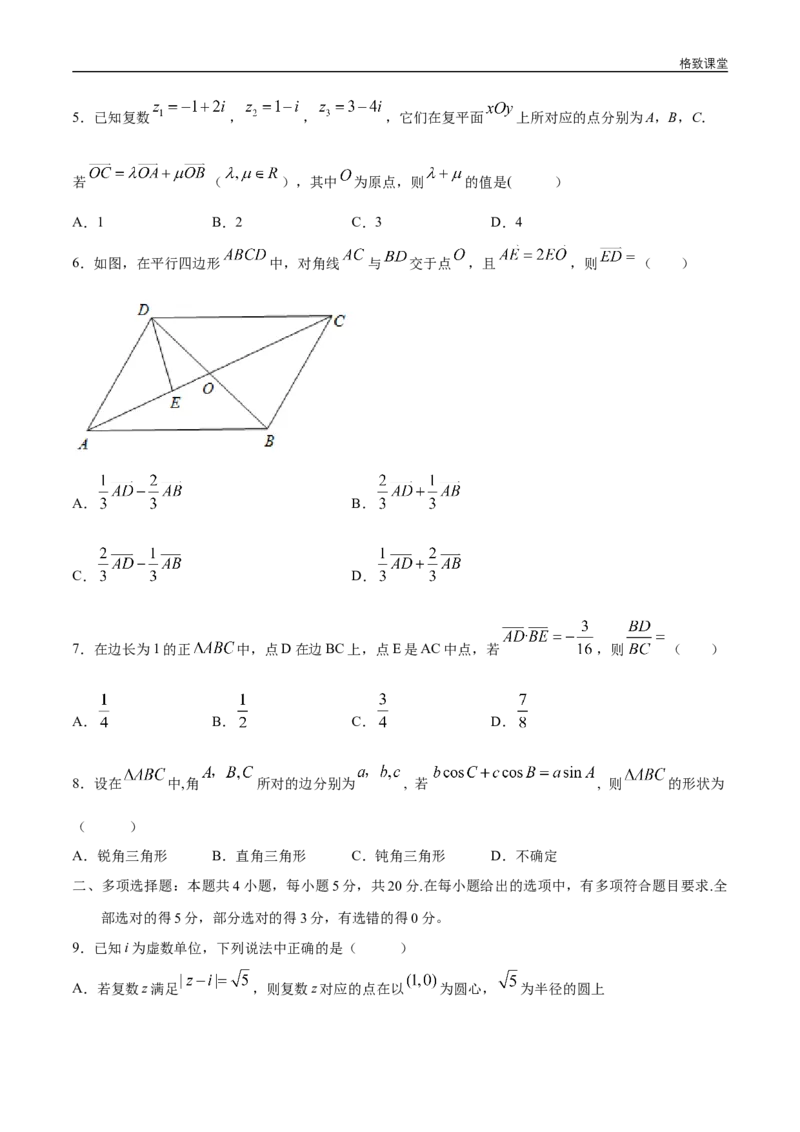
6.如图,在平行四边形 中,对角线 与 交于点 ,且 ,则 ( )
A. B.
C. D.
7.在边长为1的正 中,点D在边BC上,点E是AC中点,若 ,则 ( )
A. B. C. D.
8.设在 中,角 所对的边分别为 , 若 , 则 的形状为
( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.不确定
二、多项选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全
部选对的得5分,部分选对的得3分,有选错的得0分。
9.已知i为虚数单位,下列说法中正确的是( )
A.若复数z满足 ,则复数z对应的点在以 为圆心, 为半径的圆上格致课堂
B.若复数z满足 ,则复数
C.复数的模实质上就是复平面内复数对应的点到原点的距离,也就是复数对应的向量的模
D.复数 对应的向量为 ,复数 对应的向量为 ,若 ,则
10. 是边长为2的等边三角形,已知向量 满足 , ,则下列结论中正确的是(
)
A. 为单位向量 B. 为单位向量 C. D.
11.点O在 所在的平面内,则以下说法正确的有( )
A.若 ,则点O为 的重心
B.若 ,则点O为 的垂心
C.若 ,则点O为 的外心
D.若 ,则点O为 的内心
12.在 中, 分别是角 的对边, 为钝角,且 ,则下列结论中正确的
是( )
A. B. C. D.
三、填空题:本题共4小题,每小题5分,共20分.
13.已知复数 ( 为虚数单位, )是纯虚数,则 的虚部为______.
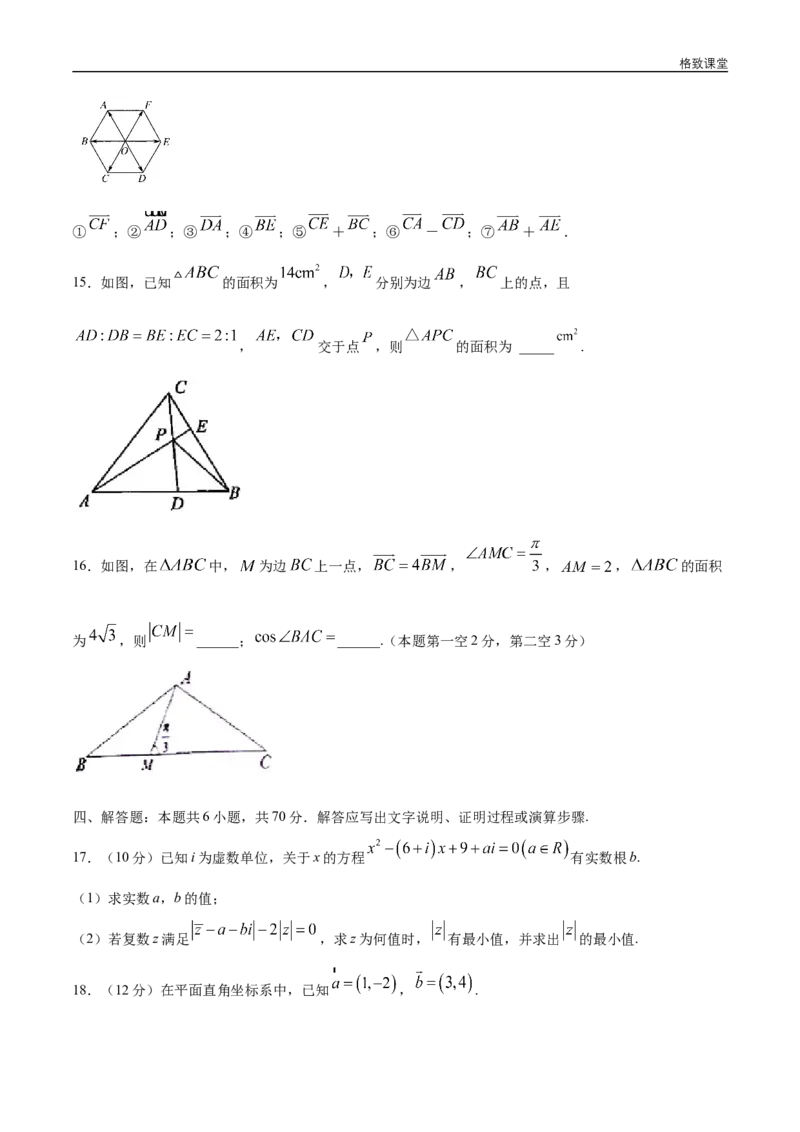
14.已知如图,在正六边形ABCDEF中,与 - + 相等的向量有____.格致课堂
① ;② ;③ ;④ ;⑤ + ;⑥ - ;⑦ + .
15.如图,已知 的面积为 , 分别为边 , 上的点,且
, 交于点 ,则 的面积为 _____ .
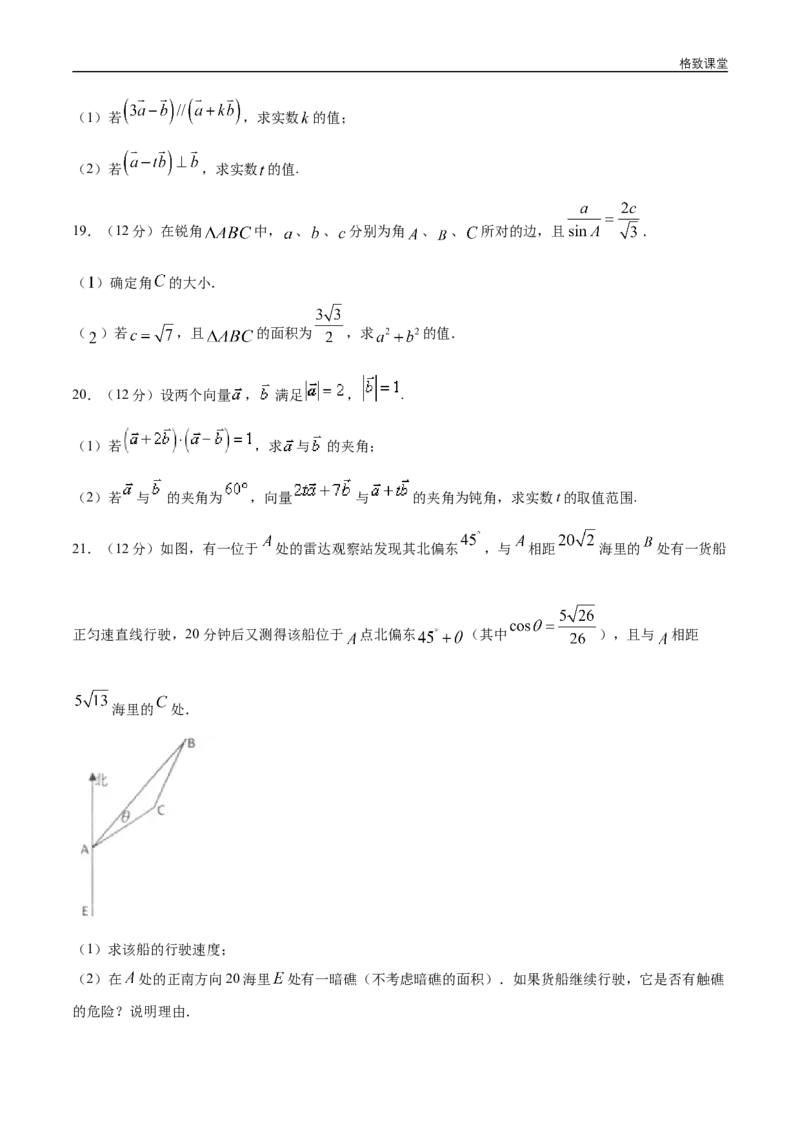
16.如图,在 中, 为边 上一点, , , , 的面积
为 ,则 ______; ______.(本题第一空2分,第二空3分)
四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
17.(10分)已知i为虚数单位,关于x的方程 有实数根b.
(1)求实数a,b的值;
(2)若复数z满足 ,求z为何值时, 有最小值,并求出 的最小值.
18.(12分)在平面直角坐标系中,已知 , .格致课堂
(1)若 ,求实数 的值;
(2)若 ,求实数 的值.
19.(12分)在锐角 中, 、 、 分别为角 、 、 所对的边,且 .
( )确定角 的大小.
( )若 ,且 的面积为 ,求 的值.
20.(12分)设两个向量 , 满足 , .
(1)若 ,求 与 的夹角;
(2)若 与 的夹角为 ,向量 与 的夹角为钝角,求实数t的取值范围.
21.(12分)如图,有一位于 处的雷达观察站发现其北偏东 ,与 相距 海里的 处有一货船
正匀速直线行驶,20分钟后又测得该船位于 点北偏东 (其中 ),且与 相距
海里的 处.
(1)求该船的行驶速度;
(2)在 处的正南方向20海里 处有一暗礁(不考虑暗礁的面积).如果货船继续行驶,它是否有触礁
的危险?说明理由.格致课堂
22.(12分)现给出两个条件:① ,② ,从中选出一
个条件补充在下面的问题中,并以此为依据求解问题:(选出一种可行的条件解答,若两个都选,则按第
一个解答计分)在 中, 分别为内角 所对的边,
(1)求 ;
(2)若 ,求 面积的最大值.