文档内容
格致课堂
绝密★启用前
2019-2020学年度第二学期期中考试试卷(基础卷)
考试时间:120分钟;考试总分:150分
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
第I卷(选择题)
一、单选题(每题5分,总分60分.)
1.已知复数 ( 为虚数单位),则复数 的虚部是( )
A.1 B.-1 C. D.
【答案】B
【解析】∵ ,
∴复数 的虚部是 ,故选:B.
2.设非零向量 , 满足 ,则( )
A. B. C. // D.
【答案】A
【解析】由 的几何意义知,以向量 , 为邻边的平行四边形为矩形,所以 .故选:
A.
3.设z=-3+2i,则在复平面内 对应的点位于
A.第一象限 B.第二象限
C.第三象限 D.第四象限
【答案】C
【解析】由 得 则 对应点(-3,-2)位于第三象限.故选C.格致课堂
4.已知复数 和复数 ,则 为
A. B. C. D.
【答案】C
【解析】zz=(cos23°+isin23°)•(cos37°+isin37°)=cos60°+isin60°= .
1 2
故答案为C.
5.已知复数z=2+i,则
A. B. C.3 D.5
【答案】D
【解析】∵ 故选D.
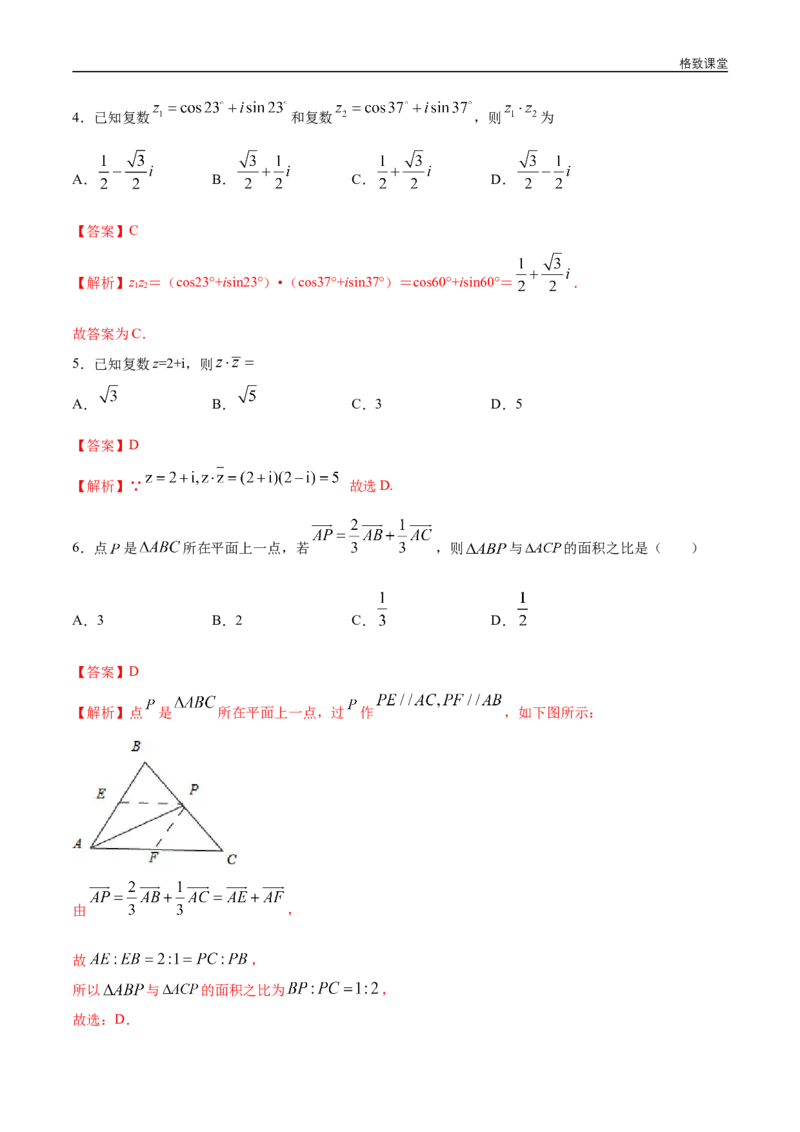
6.点 是 所在平面上一点,若 ,则 与 的面积之比是( )
A.3 B.2 C. D.
【答案】D
【解析】点 是 所在平面上一点,过 作 ,如下图所示:
由 ,
故 ,
所以 与 的面积之比为 ,
故选:D.格致课堂
7.设复数z满足(1+i)z=2i,则|z|=( )
A. B.
C. D.2
【答案】C
【解析】题意, ,所以 .故选:C.
8.已知 ,且 ,则 ( )
A.4 B.3 C. D.
【答案】C
【解析】因为 ,故 ,所以 ,
故 ,故 .故选C.
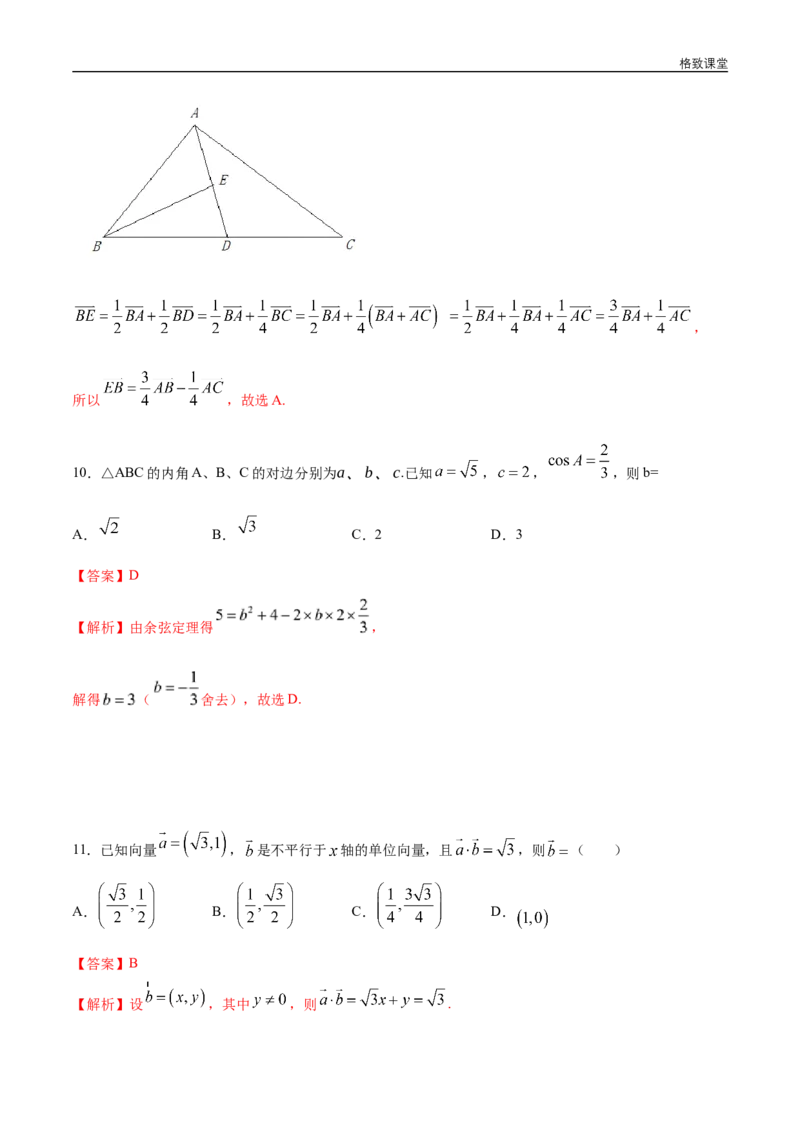
9.在△ 中, 为 边上的中线, 为 的中点,则
A. B.
C. D.
【答案】A
【解析】根据向量的运算法则,可得格致课堂
,
所以 ,故选A.
10.△ABC的内角A、B、C的对边分别为a、b、c.已知 , , ,则b=
A. B. C.2 D.3
【答案】D
【解析】由余弦定理得 ,
解得 ( 舍去),故选D.
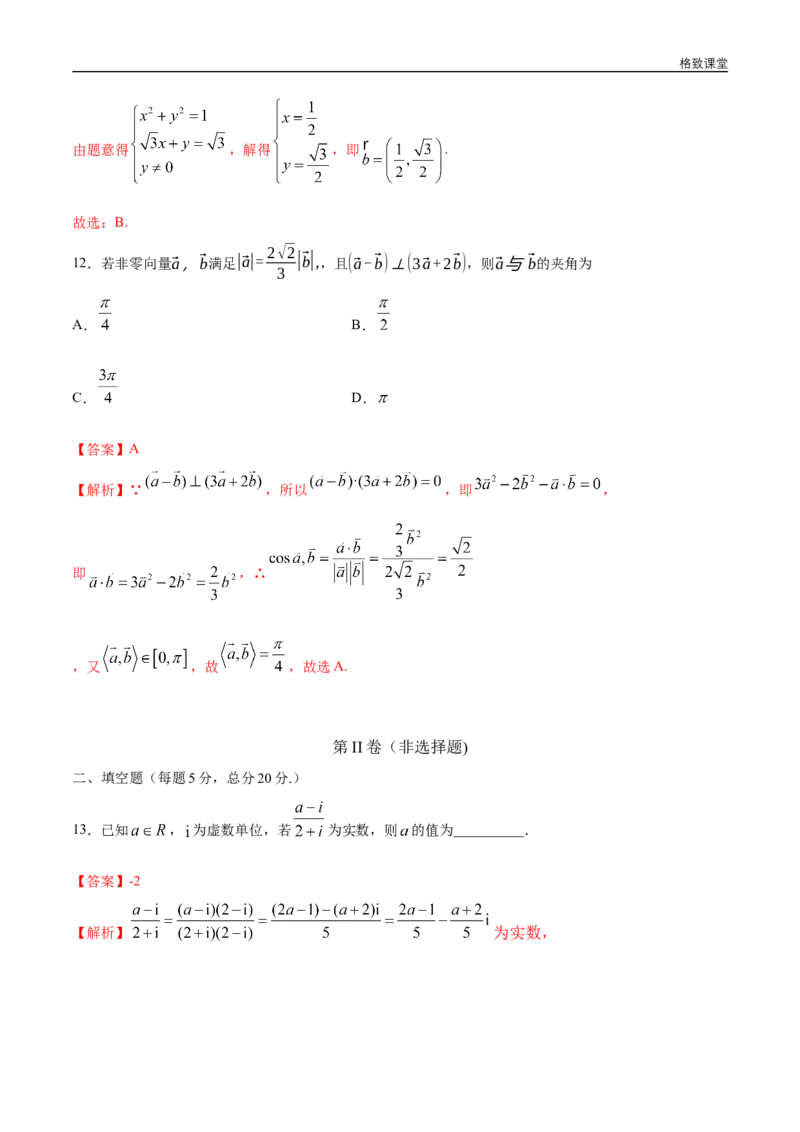
11.已知向量 , 是不平行于 轴的单位向量,且 ,则 ( )
A. B. C. D.
【答案】B
【解析】设 ,其中 ,则 .格致课堂
由题意得 ,解得 ,即 .
故选:B.
2√2
12.若非零向量⃗a,⃗b满足|⃗a|= |⃗b|,,且(⃗a-⃗b)⊥(3⃗a+2⃗b),则⃗a与⃗b的夹角为
3
A. B.
C. D.
【答案】A
【解析】∵ ,所以 ,即 ,
即 ,∴
,又 ,故 ,故选A.
第II卷(非选择题)
二、填空题(每题5分,总分20分.)
13.已知 , 为虚数单位,若 为实数,则 的值为__________.
【答案】-2
【解析】 为实数,格致课堂
则 .
14.如图,一辆汽车在一条水平的公路上向正西行驶,到A处时测得公路北侧一山顶D在西偏北30∘的方
向上,行驶600m后到达B处,测得此山顶在西偏北75∘的方向上,仰角为30∘,则此山的高度CD=
________ m.
【答案】100√6
【解析】题设可知在 中, ,由此可得 ,由正弦定理可得
,解之得 ,又因为 ,所以 ,应填
100√6.
15.平面向量 , , ( R),且 与 的夹角等于 与 的夹角,则
.
【答案】2
【解析】 , 与 的夹角等于 与 的夹角,所以
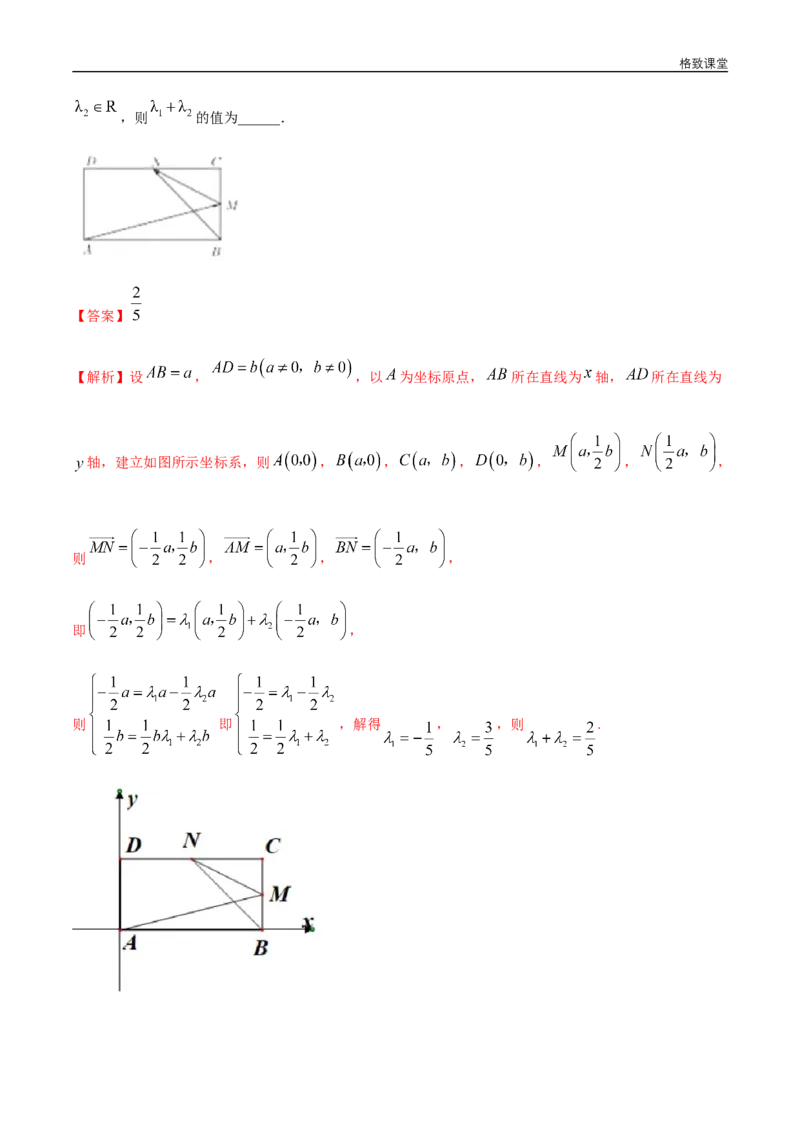
16.如图,在长方形ABCD中,M,N分别为线段BC,CD的中点,若 , ,格致课堂
,则 的值为______.
【答案】
【解析】设 , ,以 为坐标原点, 所在直线为 轴, 所在直线为
轴,建立如图所示坐标系,则 , , , , , ,
则 , , ,
即 ,
则 即 ,解得 , ,则 .格致课堂
三、解答题(17题10分,18-22题各12分,总分70分.)
17.计算:(1) ;
(2) ;
(3) .
【答案】(1)1+i(2)6-2i(3)
【解析】(1)原式 .
(2)原式 .
(3)原式 .
18.已知复数 ( ).
(1)若复数z为纯虚数,求实数m的值;
(2)若复数z在复平面内对应的点在第二象限,求实数m的取值范围.
【答案】(1) (2)(2,3)
【解析】(1)因为复数 为纯虚数,所以 ,
解之得, .
(2)因为复数 在复平面内对应的点在第二象限,所以 ,
解之得 ,得 .
所以实数 的取值范围为(2,3).
19.如图所示,平行四边形AOBD中,设向量 , ,且 , ,用格致课堂
表示 、 、 .
【答案】
【解析】 = - =a-b
∴ = + = + = + = 得a+ b.
又 =a+b. = + = + = = a+ b,
∴ = - = a+ b- a- b= a- b.
20.在平面直角坐标系中,已知 , .
(Ⅰ)若 ,求实数 的值;
(Ⅱ)若 ,求实数 的值.
【答案】(Ⅰ) ;(Ⅱ) .
【解析】(Ⅰ) , , ,
,
, ,解得 ;
(Ⅱ) ,
, ,解得 .格致课堂
21.在 中, .
(1)求 的值;
(2)若 ,求 以及 的值.
【答案】(1) ;(2)7, .
【解析】(1)由余弦定理及已知得: .
(2)因为 为三角形内角,
所以 ,
,
由正弦定理得: ,
又∵ .
,解得 或 (舍).
.
22.在 中,角 所对的边分别为 ,已知 .
(1)求角 的大小;格致课堂
(2)若 ,求 的取值范围.
【答案】(1) ;(2)
【解析】(1)∵ ,
∴ ,
即 ,
∵ ,∴ ,∴ .
(2)
,
∴ ,又 ,
∴ 的取值范围是 .