文档内容
高一数学
2024.7
本试卷共4页.满分150分.考试时间120分钟.
注意事项:
1.答题前,考生务必在试题卷、答题卡规定的地方填写自己的准考证号、姓名.
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑.如需改动,
用橡皮擦干净后,再选涂其它答案标号.回答非选择题时,将答案写在答题卡上.写在本试卷上
无效.
3.考试结束,考生必须将试题卷和答题卡一并交回.
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是
符合题目要求的.
1. 若 ,则 ( )
A. B. C. D.
2. 下列四个函数中,以 为最小正周期,且在区间 上单调递减的是( )
A. B. C. D.
.
3 已知 ,则 ( )
A. 4 B. C. D. 3
4. 如图是一个盛满水的正四棱台容器,它的下底面边长是上底面边长的2倍,高为 ,现将四棱台中的水
全部倒入与棱台等高且底面边长等于棱台下底面边长的正四棱柱容器中(损耗忽略不计),则四棱柱中水
的高度为( )
第1页/共9页
学科网(北京)股份有限公司A. B. C. D.
5. 已知 , ,且 在 上的投影的数量为 ,则 ( )
A. B. C. D.
6. 已知 ,则 ( )
A. B. C. D.
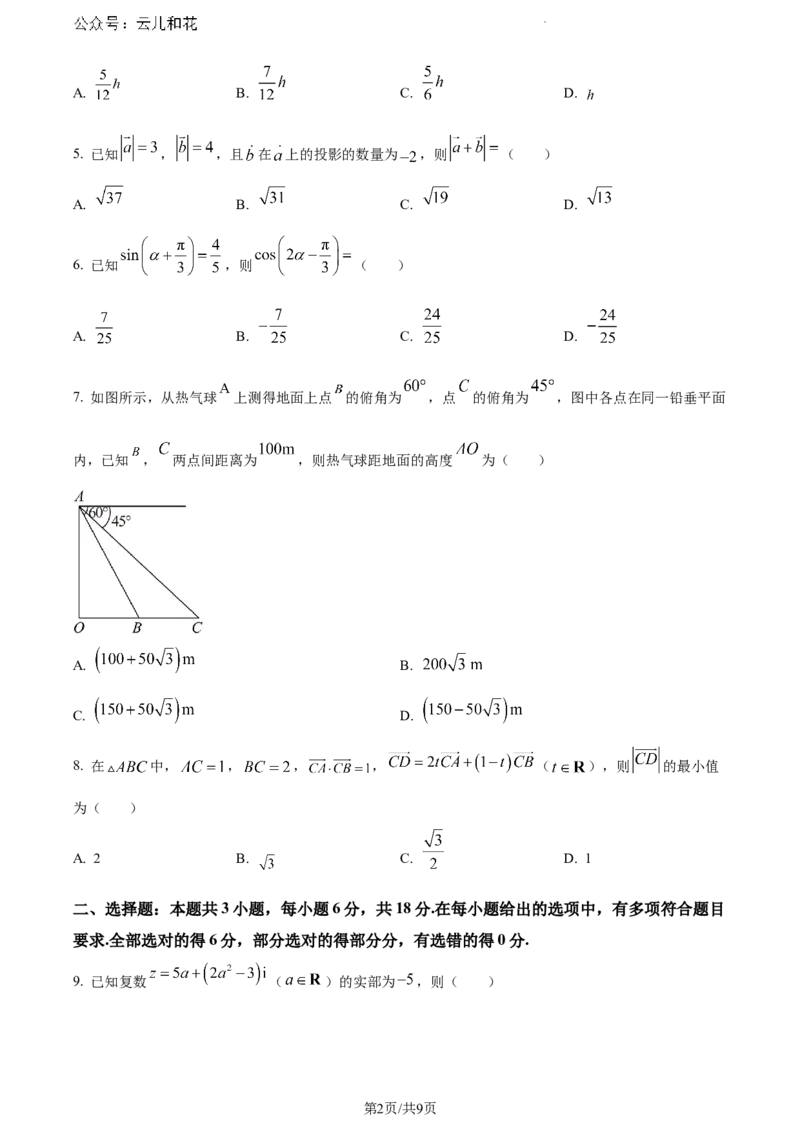
7. 如图所示,从热气球 上测得地面上点 的俯角为 ,点 的俯角为 ,图中各点在同一铅垂平面
内,已知 , 两点间距离为 ,则热气球距地面的高度 为( )
A. B.
C. D.
8. 在 中, , , , ( ),则 的最小值
为( )
A. 2 B. C. D. 1
二、选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目
要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.
9. 已知复数 ( )的实部为 ,则( )
第2页/共9页
学科网(北京)股份有限公司A. 复数 的共轭复数 B.
C. D. 在复平面内对应的点位于第三象限
.
10 函数 ,则( )
A. 的最小正周期为 B. 的图象关于 对称
C. 在 上单调递增 D. 当 时, 的值域为
11. 南宋数学家秦九韶在《数书九章》中提出“三斜求积术”,即以小斜幂并大斜幂减中斜幂,余半之,自
乘于上;以小斜幂乘大斜幂减上,余四约之,为实;一为从隅,开平方得积.可用公式
(其中 , , , 为三角形的三边和面积)表示.在 中, ,
, 分别为角 , , 所对的边,若 ,且 ,则( )
A.
的
B. 面积 最大值是
C. 当 的面积最大时,其内切圆半径为
D. 若角 的平分线 与边 相交于点 ,则 的取值范围为
三、填空题:本题共3小题,每小题5分,共15分.
12. 函数 的图象关于点 中心对称,则常数 的一个取值为______.
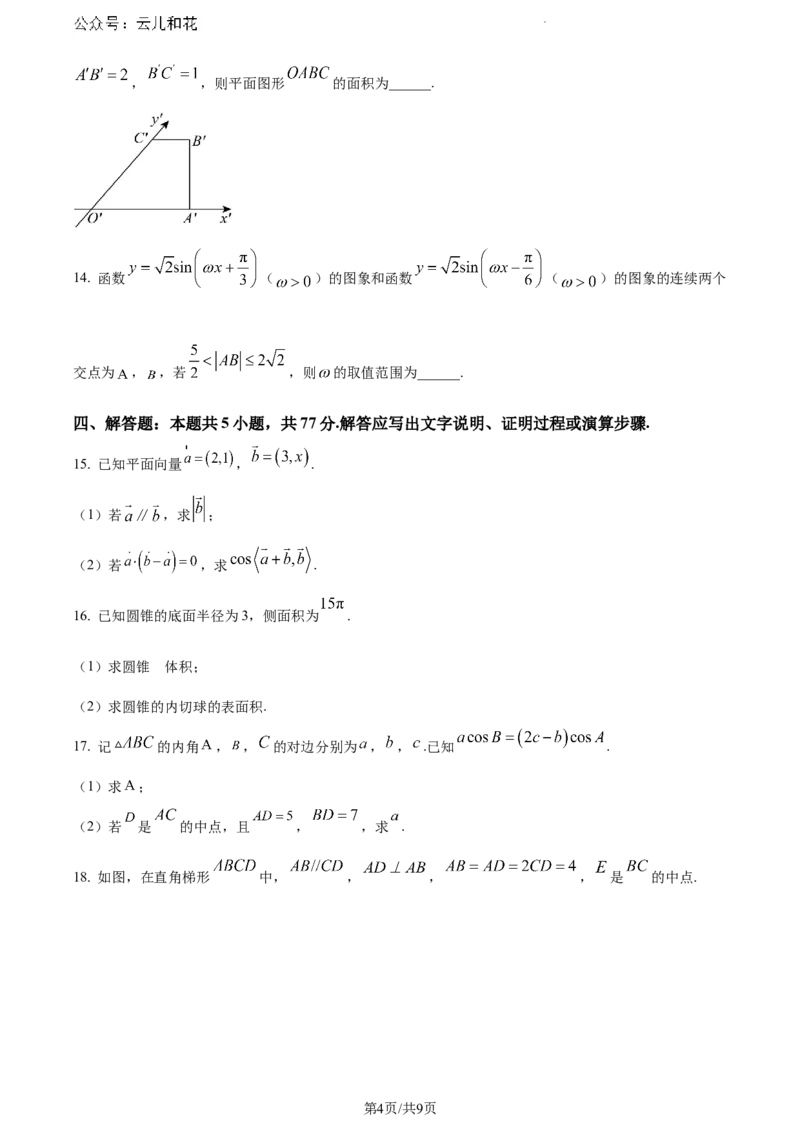
13. 如图,一个水平放置的平面图形 按斜二测画法得到的直观图 是直角梯形,又知
第3页/共9页
学科网(北京)股份有限公司, ,则平面图形 的面积为______.
14. 函数 ( )的图象和函数 ( )的图象的连续两个
交点为 , ,若 ,则 的取值范围为______.
四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.
15. 已知平面向量 , .
(1)若 ,求 ;
(2)若 ,求 .
16. 已知圆锥的底面半径为3,侧面积为 .
的
(1)求圆锥 体积;
(2)求圆锥的内切球的表面积.
17. 记 的内角 , , 的对边分别为 , , .已知 .
(1)求 ;
(2)若 是 的中点,且 , ,求 .
18. 如图,在直角梯形 中, , , , 是 的中点.
第4页/共9页
学科网(北京)股份有限公司(1)求 ;
(2)连接 ,交 于点 ,求 ;
(3)若 , , ,…, 为 边上的 等分点,当 时,求
的值.
19. 设 为坐标原点,定义非零向量 的“相伴函数”为 ( ),
称为函数 的“相伴向量”.
(1)若函数 ,求函数 的“相伴向量” ;
(2)若函数 为向量 的“相伴函数”,将函数 图象上的所有点纵坐标不变,
横坐标变为原来的 ,再将所得图象向左平移 个单位,得到函数 的图象,若函数
在 上有三个不同零点 , , ,且 .
①求实数 取值范围;
②若 ,求实数 的取值范围.
第5页/共9页
学科网(北京)股份有限公司第6页/共9页
学科网(北京)股份有限公司高一数学
2024.7
本试卷共4页.满分150分.考试时间120分钟.
注意事项:
1.答题前,考生务必在试题卷、答题卡规定的地方填写自己的准考证号、姓名.
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑.如需改动,
用橡皮擦干净后,再选涂其它答案标号.回答非选择题时,将答案写在答题卡上.写在本试卷上
无效.
3.考试结束,考生必须将试题卷和答题卡一并交回.
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是
符合题目要求的.
【1题答案】
【答案】A
【2题答案】
【答案】D
【3题答案】
【答案】C
【4题答案】
【答案】B
【5题答案】
【答案】D
【6题答案】
【答案】A
【7题答案】
【答案】C
【8题答案】
【答案】B
二、选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目
要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.
【9题答案】
【答案】BD
第7页/共9页
学科网(北京)股份有限公司【10题答案】
【答案】ABD
【11题答案】
【答案】ACD
三、填空题:本题共3小题,每小题5分,共15分.
【12题答案】
【答案】 (答案不唯一,满足 即可)
【13题答案】
【答案】
【14题答案】
【答案】
四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.
【15题答案】
【答案】(1)
(2)
【16题答案】
【答案】(1)
(2)
【17题答案】
【答案】(1)
(2)
【18题答案】
【答案】(1)
第8页/共9页
学科网(北京)股份有限公司(2)
(3)
【19题答案】
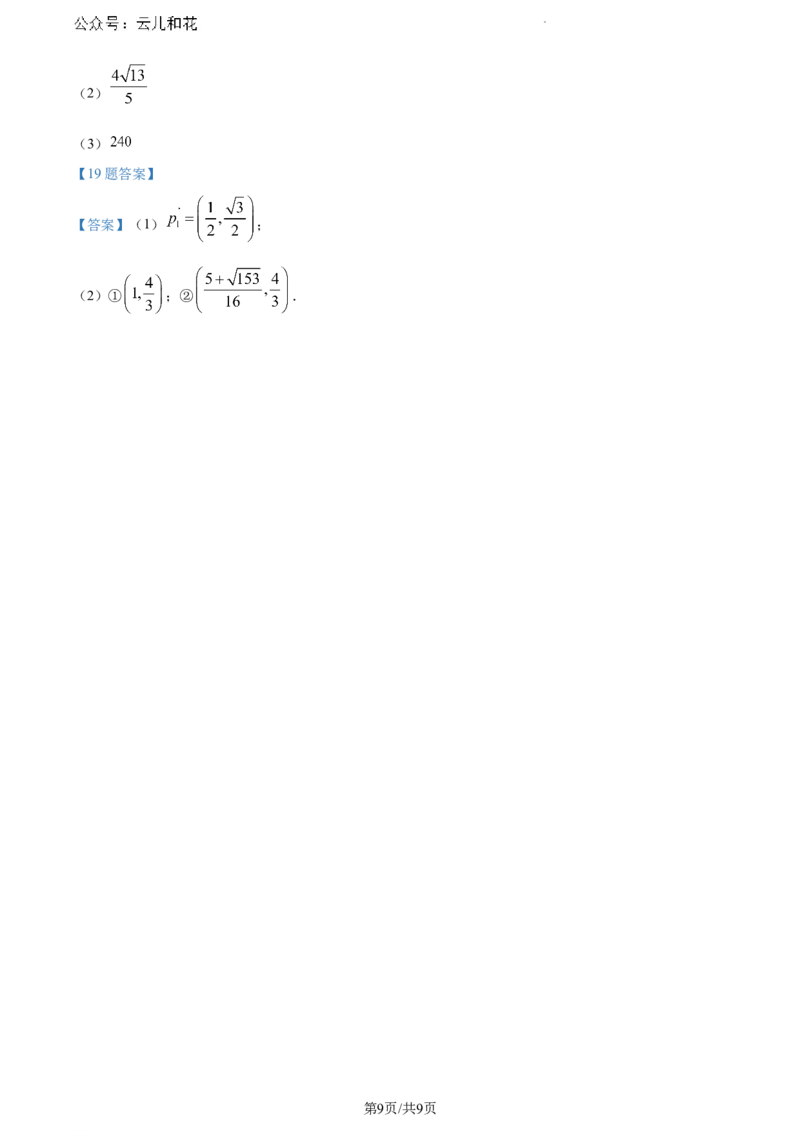
【答案】(1) ;
(2)① ;② .
第9页/共9页
学科网(北京)股份有限公司