文档内容
期中押题模拟卷03
(考试时间:120分钟 试卷满分:150分)
注意事项:
1.本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.答卷前,考生务必将自己的姓名、准
考证号填写在答题卡上.
2.回答第Ⅰ卷时,选出每小题答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑.如需改动,
用橡皮擦干净后,再选涂其他答案标号.写在本试卷上无效.
3.回答第Ⅱ卷时,将答案写在答题卡上.写在本试卷上无效.
4.测试范围:选择性必修第一册
5.考试结束后,将本试卷和答题卡一并交回.
第Ⅰ卷
一、选择题:本题共8小题,每小题5分,共40分。在每小题给出的四个选项中,只有一项是符合题目要
求的。
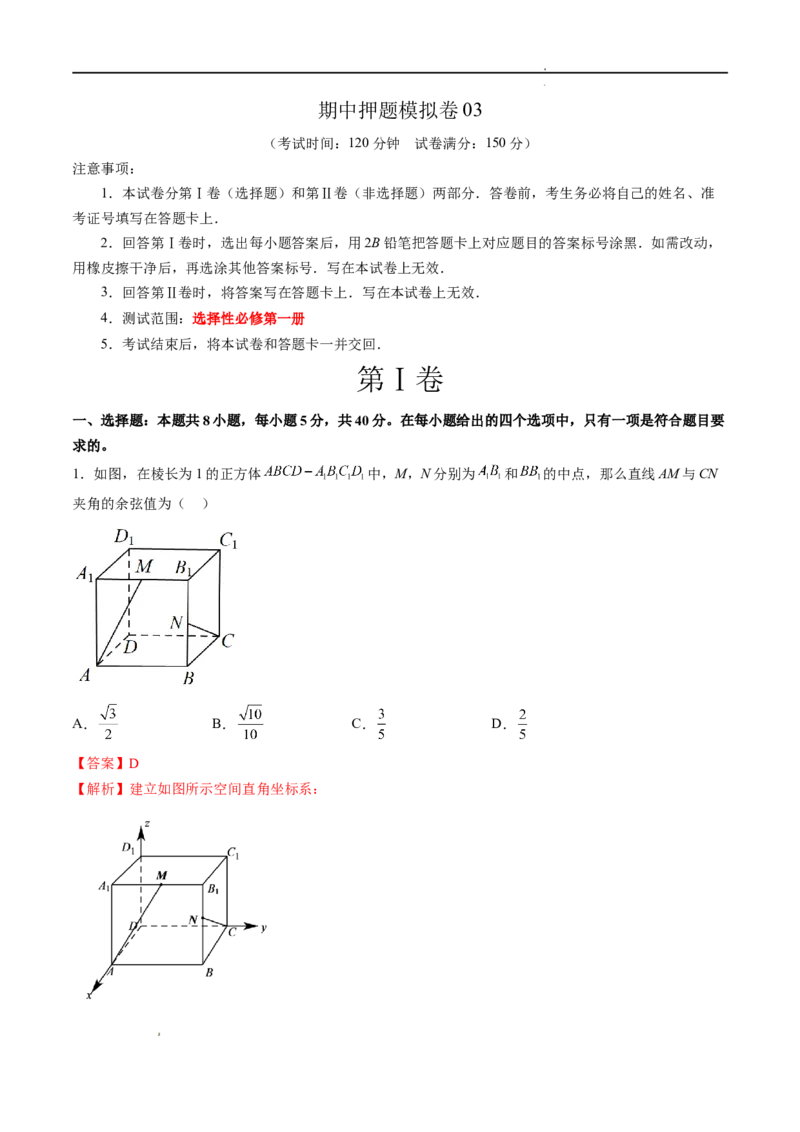
1.如图,在棱长为1的正方体 中,M,N分别为 和 的中点,那么直线AM与CN
夹角的余弦值为( )
A. B. C. D.
【答案】D
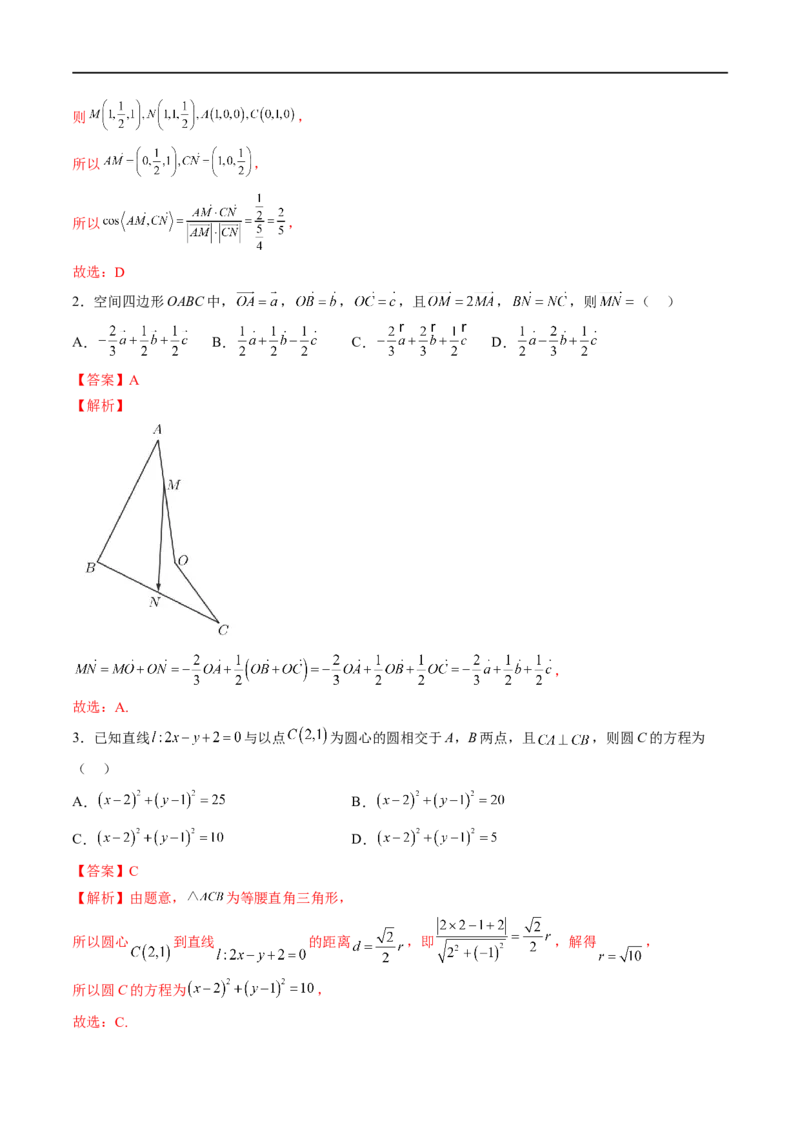
【解析】建立如图所示空间直角坐标系:
学学学科科科网网网(((北北北京京京)))股股股份份份有有有限限限公公公司司司则 ,
所以 ,
所以 ,
故选:D
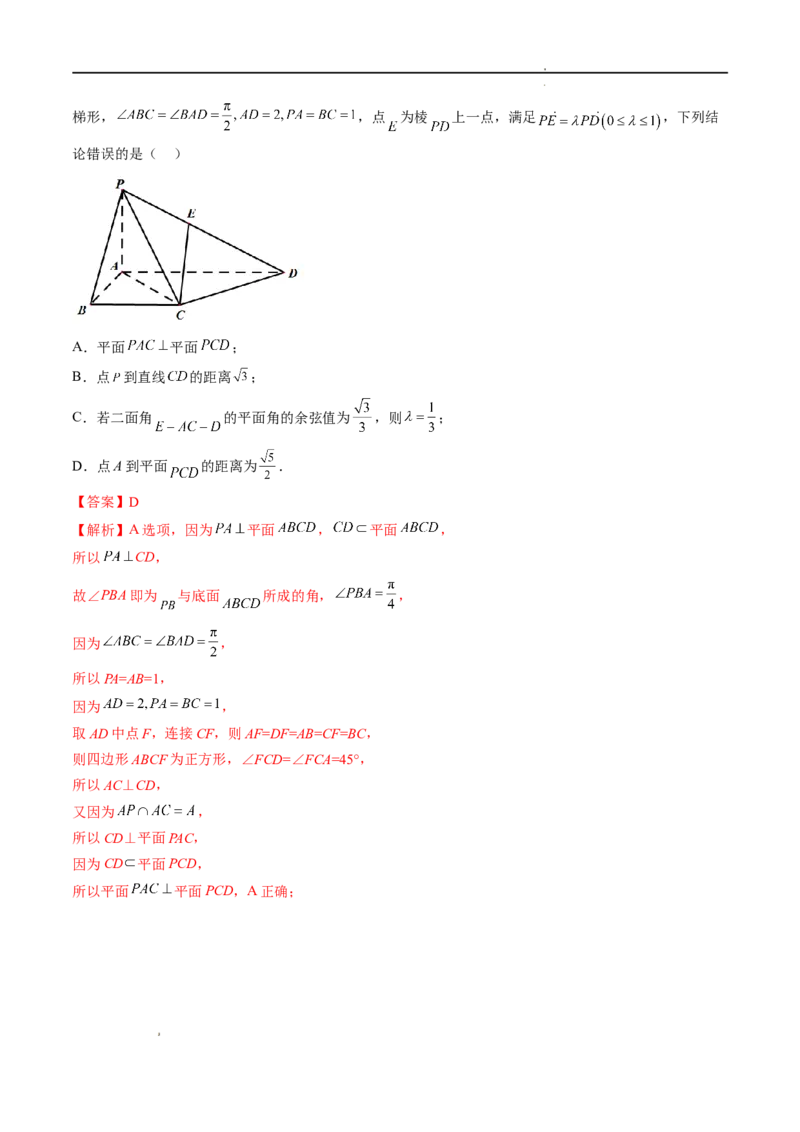
2.空间四边形OABC中, , , ,且 , ,则 ( )
A. B. C. D.
【答案】A
【解析】
,
故选:A.
3.已知直线 与以点 为圆心的圆相交于A,B两点,且 ,则圆C的方程为
( )
A. B.
C. D.
【答案】C
【解析】由题意, 为等腰直角三角形,
所以圆心 到直线 的距离 ,即 ,解得 ,
所以圆C的方程为 ,
故选:C.4.椭圆 的焦点为 、 ,椭圆上的点 满足 ,则 ( )
A. B. C. D.
【答案】C
【解析】 椭圆 的焦点为 、 ,椭圆上的点 满足 ,
由椭圆定义得: ,
,①
由余弦定理得: ,②
联立①②,得: ,
∴ ,
故选:C.
5.已知A,B,C是椭圆 上不同的三点,且原点O是△ABC的重心,若点C的坐
标为 ,直线AB的斜率为 ,则椭圆 的离心率为( )
A. B. C. D.
【答案】B
【解析】设 的中点 ,
因为原点O是△ABC的重心,所以 三点共线,
所以 ,
由于 ,所以 ,
故选:B.
6.已知O为坐标原点,设F,F 分别是双曲线x2-y2=1的左、右焦点,P为双曲线左支上任意一点,过
1 2
点F 作∠FPF 的平分线的垂线,垂足为H,则|OH|=( )
1 1 2
A.1 B.2
C.4 D.
【答案】A
【解析】如图所示,
学学学科科科网网网(((北北北京京京)))股股股份份份有有有限限限公公公司司司延长FH交PF 于点Q,由PH为∠FPF 的平分线及PH⊥FQ,易知 ,所以|PF|=|PQ|.
1 2 1 2 1 1
根据双曲线的定义,得|PF|-|PF|=2,即|PF|-|PQ|=2,
2 1 2
从而|QF|=2.
2
在△FQF 中,易知OH为中位线,则|OH|=1.
1 2
故选:A.
7.如图,点A,B,C在抛物线 上,抛物线的焦点F在 上, 与x轴交于点D, ,
,则 ( )
A. B.4 C. D.3
【答案】B
【解析】依题意设 ,则直线AB,AC,BC斜率分别为:
,
因 ,则 ,即 ,
则 ,因F(1,0)在直线AB上,则 ,而 ,
有 ,即 ,点A在直线 上,
又 是等腰三角形,点F,点D关于直线 对称,所以点D坐标为(5,0),|FD|=4.
故选:B
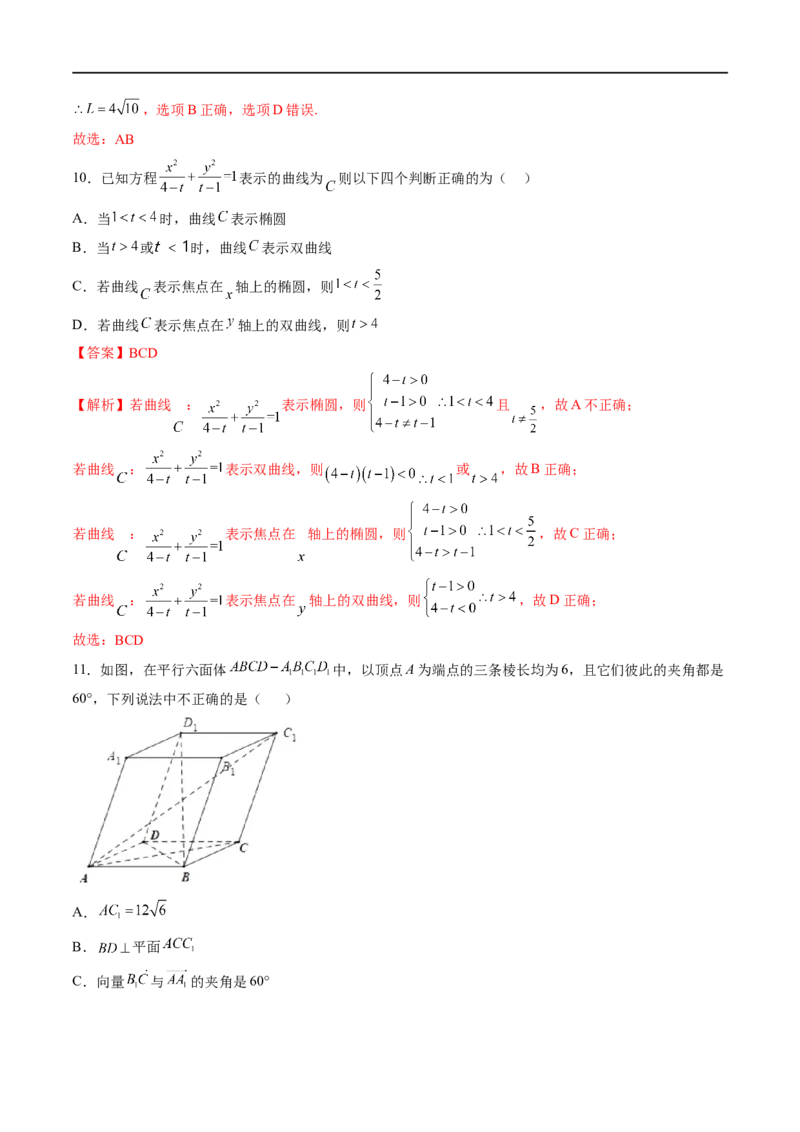
8.如图,在四棱锥 中, 平面 , 与底面 所成的角为 ,底面 为直角梯形, ,点 为棱 上一点,满足 ,下列结
论错误的是( )
A.平面 平面 ;
B.点 到直线 的距离 ;
C.若二面角 的平面角的余弦值为 ,则 ;
D.点A到平面 的距离为 .
【答案】D
【解析】A选项,因为 平面 , 平面 ,
所以 CD,
故∠PBA即为 与底面 所成的角, ,
因为 ,
所以PA=AB=1,
因为 ,
取AD中点F,连接CF,则AF=DF=AB=CF=BC,
则四边形ABCF为正方形,∠FCD=∠FCA=45°,
所以AC⊥CD,
又因为 ,
所以CD⊥平面PAC,
因为CD 平面PCD,
所以平面 平面PCD,A正确;
学学学科科科网网网(((北北北京京京)))股股股份份份有有有限限限公公公司司司由A选项的证明过程可知:CD⊥平面PAC,
因为 平面PAC
所以CD⊥PC,
故点P到直线CD的距离即为PC的长度,
其中
由勾股定理得: ,B正确;
以A为坐标原点,AB所在直线为x轴,AD所在直线为y轴,AP所在直线为z轴,建立空间直角坐标系,
则 , , , ,
其中平面ACD的法向量为 ,设平面ACE的法向量为 ,
则 ,令 得: ,所以 ,
设二面角 的平面角为 ,显然 ,
其中 ,解得: 或 ,
因为 ,所以 ,C正确;
过点A作AH⊥PC于点H,
由于CD⊥平面APC, 平面APC,
所以AH⊥CD,
因为 ,
所以AH⊥平面PCD,
故AH即为点A到平面PCD的距离,
因为PA⊥AC,
所以 ,D选项错误
故选:D
二、选择题:本题共4小题,每小题5分,共20分。在每小题给出的选项中,有多项符合题目要求。全部
选对的得5分,部分选对的得2分,有选错的得0分。
9.已知圆 : 和圆 : 则( )
A.两圆相交 B.公共弦长为
C.两圆相离 D.公切线长
【答案】AB
【解析】圆 的标准方程为: ,圆心为(5,5)半径为
圆 的标准方程为: ,圆心为(3,-1)半径为
所以两圆心的距离: ,
两圆相交,选项A正确,选项C错误;
设两圆公共弦长为L,则有:
学学学科科科网网网(((北北北京京京)))股股股份份份有有有限限限公公公司司司,选项B正确,选项D错误.
故选:AB
10.已知方程 表示的曲线为 则以下四个判断正确的为( )
A.当 时,曲线 表示椭圆
B.当 或 时,曲线 表示双曲线
C.若曲线 表示焦点在 轴上的椭圆,则
D.若曲线 表示焦点在 轴上的双曲线,则
【答案】BCD
【解析】若曲线 : 表示椭圆,则 且 ,故A不正确;
若曲线 : 表示双曲线,则 或 ,故B正确;
若曲线 : 表示焦点在 轴上的椭圆,则 ,故C正确;
若曲线 : 表示焦点在 轴上的双曲线,则 ,故D正确;
故选:BCD
11.如图,在平行六面体 中,以顶点A为端点的三条棱长均为6,且它们彼此的夹角都是
60°,下列说法中不正确的是( )
A.
B. 平面
C.向量 与 的夹角是60°D.直线 与AC所成角的余弦值为
【答案】AC
【解析】对于 ,
,
所以 ,选项 错误;
对于
,所以 ,即 ,
,所以 ,即 ,因为
, 平面 ,所以 平面 ,选项 正确;
对于 :向量 与 的夹角是 ,所以向量 与 的夹角也是 ,选项 错误;
对于 ,
所以 ,
,
同理,可得
,
所以 ,所以选项 正确.
故选:AC.
12. 为椭圆 : 上的动点,过 作 切线交圆 : 于 , ,过 , 作
切线交于 ,则( )
A. 的最大值为 B. 的最大值为
C. 的轨迹是 D. 的轨迹是
【答案】AC
【解析】根据题意,作图如下:
学学学科科科网网网(((北北北京京京)))股股股份份份有有有限限限公公公司司司不妨设点 的坐标为 ,点 坐标为 ,
故切点 所在直线方程为: ;
又点 为椭圆上的一点,
故切线方程 所在直线方程为: ;
故可得 .即
不妨设直线 交 于点 ,故
设直线 方程为: ,
故 ,又 ,
故可得三角形 的面积
,
当且仅当 ,且 时,即 时取得最大值.
因为点 在椭圆上,故 ,
又 ,故可得 ,整理得 .
故动点 的轨迹方程为: .
故选: .
第ⅠⅠ卷
三、填空题:本题共4小题,每小题5分,共20分。
13.已知直线 与圆 交于 两点,则 ________
【答案】
【解析】圆 可化为
即圆心坐标为 ,半径
圆心到直线 的距离
故
故答案为:
14.二面角的棱上有 , 两点,直线 , 分别在这个二面角的两个半平面内,且都垂直于 .已知
, , , ,则该二面角的大小为________.
【答案】
【解析】由条件,知 , ,
.
∴ .
∴ ,又∵ ,∴ ,∴二面角的大小为 .
故答案为: .
15.设抛物线 : ( )的焦点为 ,准线为 ,点 为抛物线 上一点,以 为圆心, 为半
径的圆交 于 、 两点,若 , 的面积为 ,则 _______.
【答案】
【解析】∵ ,
∴ ,
学学学科科科网网网(((北北北京京京)))股股股份份份有有有限限限公公公司司司又∵ ,∴ , ,
∴ 到准线 的距离 ,
∴ ,解得 .
故答案为:1.
16.已知 为双曲线 的右焦点,经过 作直线 与双曲线的一条渐近线垂直,垂足
为 ,直线 与双曲线的另一条渐近线在第二象限的交点为 .若 ,则双曲线的离心率为
______.
【答案】
【解析】
由题意可设: ,
由 得: ,即 ;由 得: ,即 ;
, ,即 ,
,即 , ,解得: ,
即双曲线的离心率为 .
故答案为: .
四、解答题:本题共6小题,共70分。解答应写出文字说明、证明过程或演算步棸。
17.(10分)
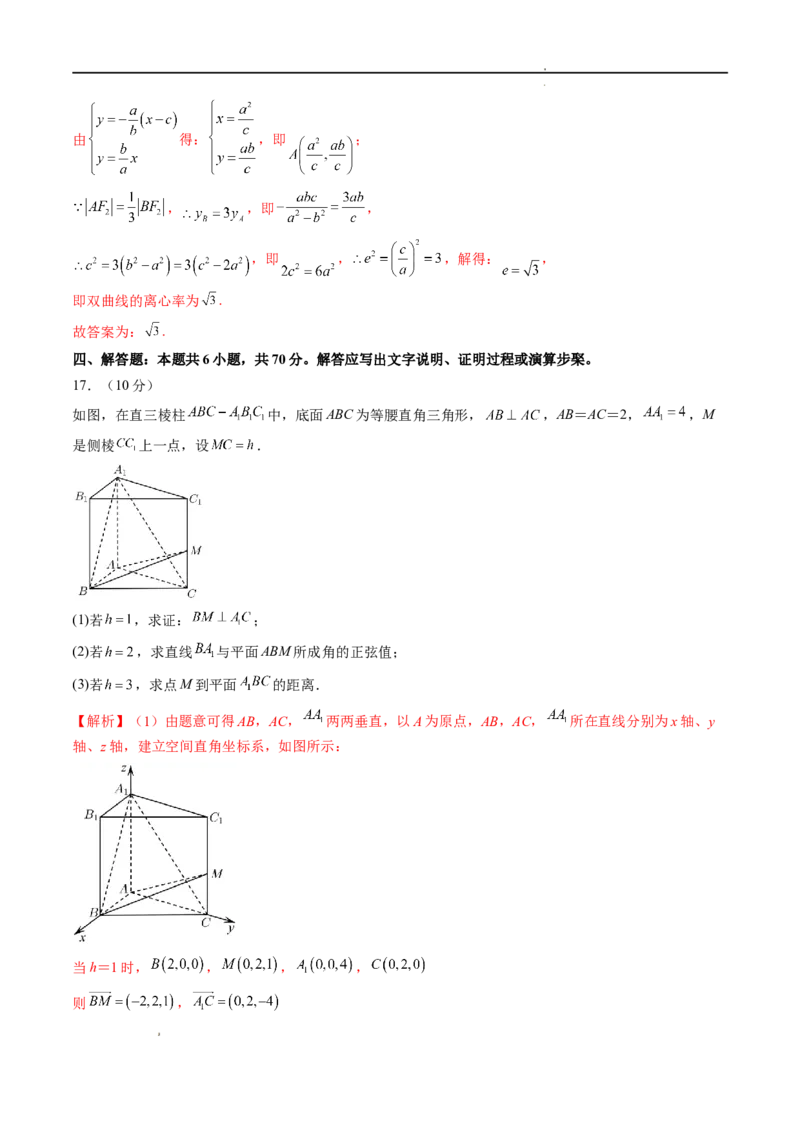
如图,在直三棱柱 中,底面ABC为等腰直角三角形, ,AB=AC=2, ,M
是侧棱 上一点,设 .
(1)若 ,求证: ;
(2)若 ,求直线 与平面ABM所成角的正弦值;
(3)若 ,求点M到平面 的距离.
【解析】(1)由题意可得AB,AC, 两两垂直,以A为原点,AB,AC, 所在直线分别为x轴、y
轴、z轴,建立空间直角坐标系,如图所示:
当h=1时, , , ,
则 ,
学学学科科科网网网(((北北北京京京)))股股股份份份有有有限限限公公公司司司∵
∴ .
(2)当h=2时, , , , ,
, , ,设平面ABM的法向量
则 ,取y=1,得 是平面ABM的一个法向量
设直线 与平面ABM所成角为
则
∴直线 与平面ABM所成角的正弦值为 .
(3)当h=3时, , , , ,
, , ,
设平面 的法向量 ,则 ,
取a=2,得 是平面 的一个法向量
∴点M到平面 的距离 .
18.(12分)
已知双曲线 的一条渐近线方程为 ,一个焦点到该渐近线的距离为1.
(1)求 的方程;
(2)经过点 的直线 交 于 两点,且 为线段 的中点,求 的方程.
【解析】(1)双曲线 的渐近线为 ,即 ,
所以 ,
又焦点 到直线 的距离 ,所以 ,
又 ,所以 , ,所以双曲线方程为(2)设 , ,直线 的斜率为 ,则 , ,
所以 , ,
两式相减得 ,即
即 ,所以 ,解得 ,
所以直线 的方程为 ,即 ,
经检验直线 与双曲线 有两个交点,满足条件,
所以直线 的方程为 .
19.(12分)
在平面直角坐标系xOy中,已知圆心在y轴上的圆C经过两点 和 ,直线 的方程为 .
(1)求圆C的方程;
(2)过点 作圆C切线,求切线方程;
(3)当 时,Q为直线 上的点,若圆C上存在唯一的点P满足 ,求点Q的坐标.
【解析】(1)设圆的方程为 ,将M,N坐标代入,得: ,
解得 ,所以圆的方程为 ;
(2)当切线斜率不存在时,直线 与圆相切;
当切线斜率存在时,设直线方程为 ,即 ,
由圆心 到直线的距离 ,
解得 ,故切线方程为 ,
综上,切线方程为 或 ;
(3)设 , ,则 ,
化简得 ,
此圆与圆C相切,
所以有 ,解得 ,
所以 或 .
20.(12分)
学学学科科科网网网(((北北北京京京)))股股股份份份有有有限限限公公公司司司如图,在三棱柱 中, , , 是 的中点,点 在平面 上的射影为
的中点.
(Ⅰ)证明: 平面 ;
(Ⅱ)若直线 与平面 所成角的正弦值为 ,求二面角 的平面角的正切值.
【解析】(Ⅰ)连结 交 于 ,连结 .
∵ 是三棱柱,∴四边形 是平行四边形.
则 .
在 中,∵ ,∴ .
又 平面 , 平面 ,∴ 平面 .
(Ⅱ)因为 平面 , 与平面 所成角为 ,即 ,
又因为在 中, ,故 , ,
在 中,由余弦定理求得 ,
过 作 , ,
分别以 、 、 作为 轴、 轴、 轴建立空间直角坐标系.
则 , , ,
, , ,
故 , ,设平面 的法向量为 ,则 .
,取 ,
又平面 的法向量为 ,
故 ,所以 ,
故 ,
即所求二面角的平面角的正切值为 .
21.(12分)
已知椭圆中心在原点,焦点在x轴上,一个顶点为 ,且其右焦点到直线 的距离为
2.
(1)求椭圆的方程;
(2)是否存在斜率为k的直线l,使l与已知椭圆交于不同的两点M,N,且 ?若存在,请求出k的
取值范围,若不存在,请说明理由.
【解析】(1)因为椭圆中心在原点,焦点在x轴上,一个顶点为A(0,-1),由题意,可设椭圆的方程
,则其右焦点 ,由F到直线 的距离d=3,解得 ,所以椭
圆的方程 .
(2)假设存在直线 符合题意.
与椭圆方程联立,得: ,消去y得: .
设
则有 ,
学学学科科科网网网(((北北北京京京)))股股股份份份有有有限限限公公公司司司所以
所以MN的中点P的坐标 .
因为AN=AM,所以AP是线MN的垂直平分线,所以AP⊥MN.
根据斜率之积为-1,可得 ,将其代入 ,
并整理得: ,解得: .
故存在满足条件的直线l,其斜率的取值范围 .
22.(12分)
如图,椭圆 的离心率是 ,短轴长为 ,椭圆的左、右顶点为 、 .过椭圆与抛
物线的公共焦点 的直线 与椭圆相交于 两点,与抛物线 相交于 两点,点 为 的中点.
(1)求椭圆 和抛物线 的方程;
(2)记 的面积为 的面积为 ,若 ,求直线 在 轴上截距的范围.
【解析】(1)根据题意得: ,解得 , , ,抛物线焦点 ,
因此椭圆 ,拋物线
(2)设 ,联立 与椭圆 ,
整理得: ,判别式:
弦长公式: ,所以联立 与抛物线 ,整理得: ,判别式:
弦长公式: ,
所以 ,
因为 ,因此 ,解得:
在 轴上截距 或 ,因此在 轴上截距取值范围是 .
学学学科科科网网网(((北北北京京京)))股股股份份份有有有限限限公公公司司司