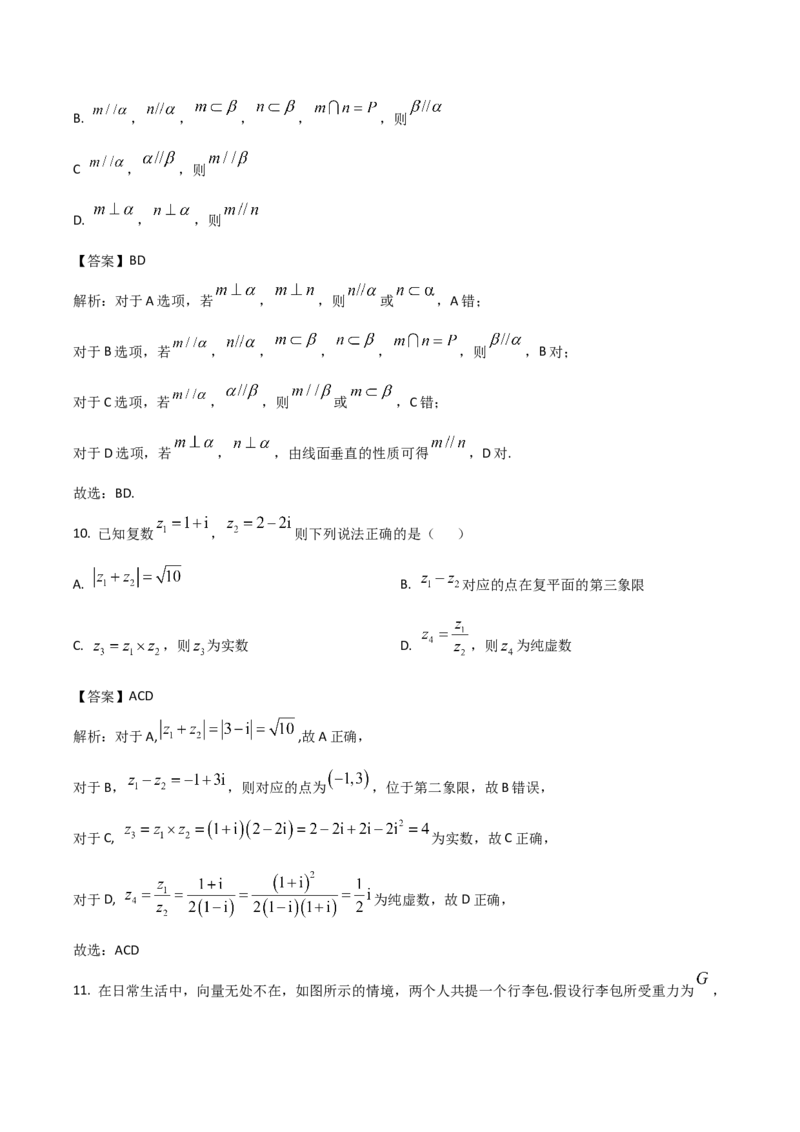文档内容
河池市 2025 年春季学期高一期末学业水平质量检测
数学
(本试卷满分150分,考试时间120分钟)
一、单选题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是
符合题目要求的.
1. 与 是共轭复数,已知复数 ,则 ( )
A. B. C. D.
【答案】A
解析:因为 ,故 .
故选:A.
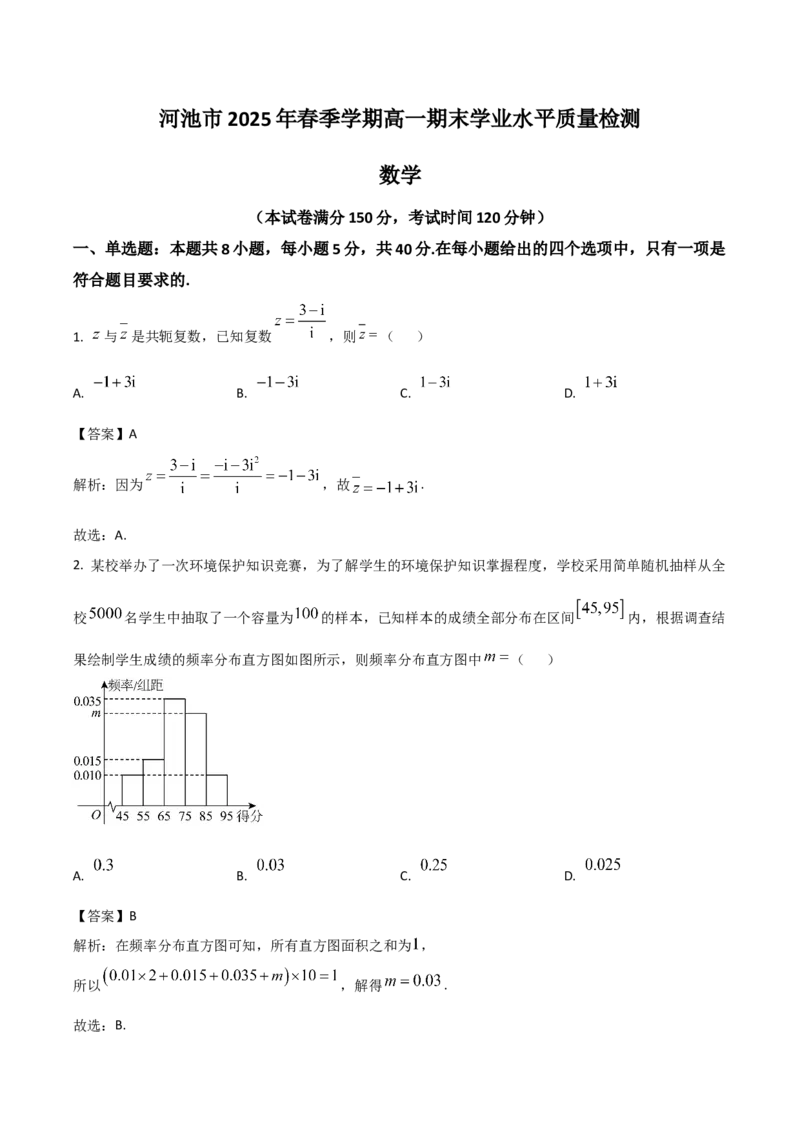
2. 某校举办了一次环境保护知识竞赛,为了解学生的环境保护知识掌握程度,学校采用简单随机抽样从全
校 名学生中抽取了一个容量为 的样本,已知样本的成绩全部分布在区间 内,根据调查结
果绘制学生成绩的频率分布直方图如图所示,则频率分布直方图中 ( )
A. B. C. D.
【答案】B
解析:在频率分布直方图可知,所有直方图面积之和为 ,
所以 ,解得 .
故选:B.3. 下列向量的概念错误的是( )
A. 长度为0的向量是零向量,零向量的方向是任意的
B. 零向量和任何向量都是共线向量
C. 相等向量一定是共线向量,但共线向量不一定相等
D. , ,则
【答案】D
解析:对于A, 零向量的长度为0,且方向是任意的,故A正确,
对于B,规定零向量与任意向量共线,故B正确,
对于C,相等向量的模长和方向都相同,故相等向量一定是共线向量,但共线向量是方向相同或者相反的
两个向量,模长不一定相等,故共线向量不一定相等,C正确,
对于D,当 为零向量时,此时不一定能得到 ,故D错误,
故选:D
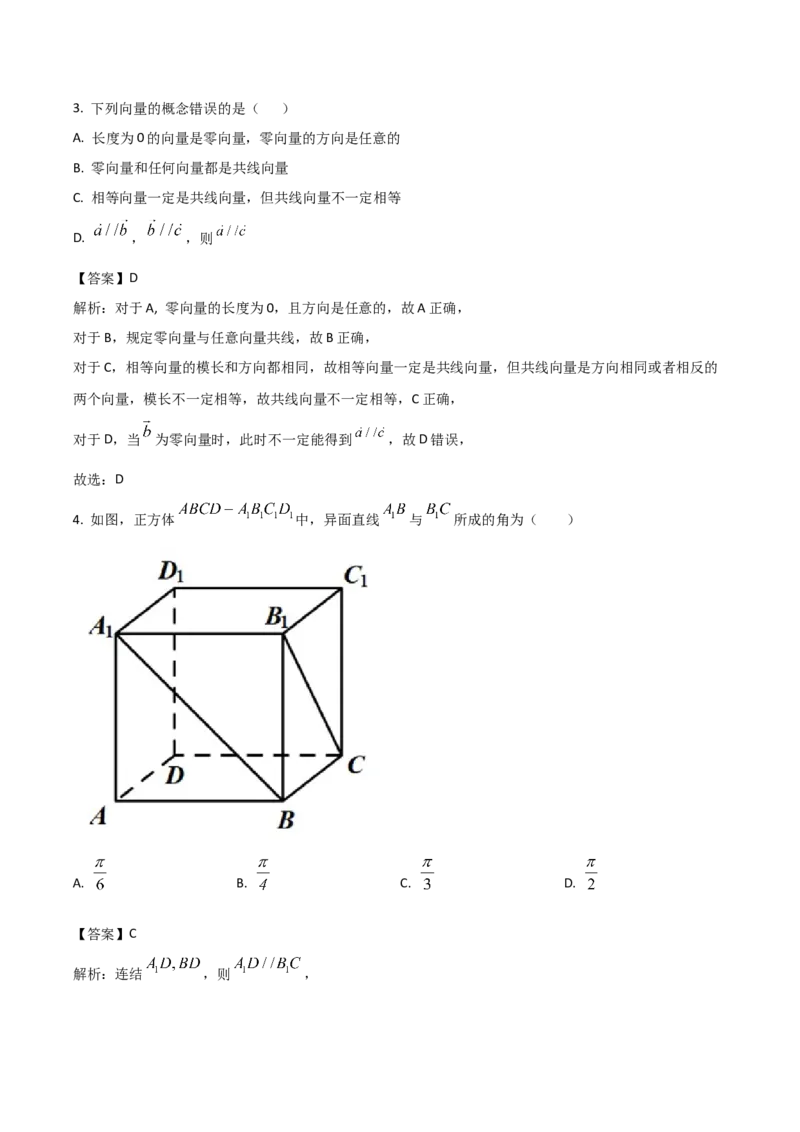
4. 如图,正方体 中,异面直线 与 所成的角为( )
A. B. C. D.
【答案】C
解析:连结 ,则 ,所以 为异面直线 与 所成的角.
在正方体中,因为 为正三角形,所以 .
故选:C.
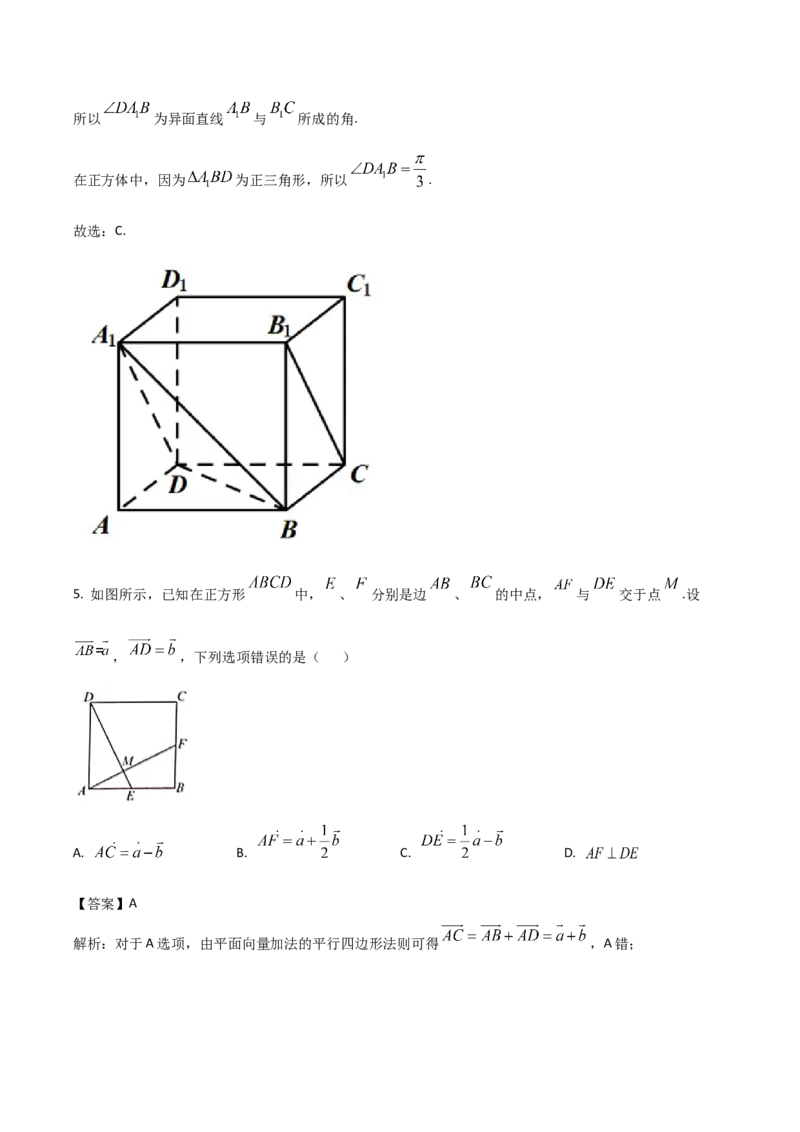
5. 如图所示,已知在正方形 中, 、 分别是边 、 的中点, 与 交于点 .设
, ,下列选项错误的是( )
A. B. C. D.
【答案】A
解析:对于A选项,由平面向量加法的平行四边形法则可得 ,A错;对于B选项, ,B对;
对于C选项, ,C对;
对于D选项,由题意可得 , ,
所以 ,故 ,D对.
故选:A.
6. 已知样本空间 ,事件 ,事件 ,则下列选项错误的是( )
A. B.
C. 事件 与事件 独立 D. 事件 与事件 互斥
【答案】D
解析:对于A, ,故A正确,
对于B, ,故B正确,
对于C,由于 ,则 ,故事件 与事件 独立,C正确,
对于D,事件 与事件 有公共的样本点 ,故不互斥,D错误,
故选:D
7. 如图,在直三棱柱 中, , , , ,点 在棱 上,
求 的最小值( )A. B. C. D.
【答案】D
解析:将平面 、平面 延展为同一个平面,如下图所示:
由图可知,当 、 、 三点共线时, 取最小值,
且 , ,且 ,
延展后, 、 、 共线,且 , , ,
由勾股定理可得 .
的
故 最小值为 .
故选:D.
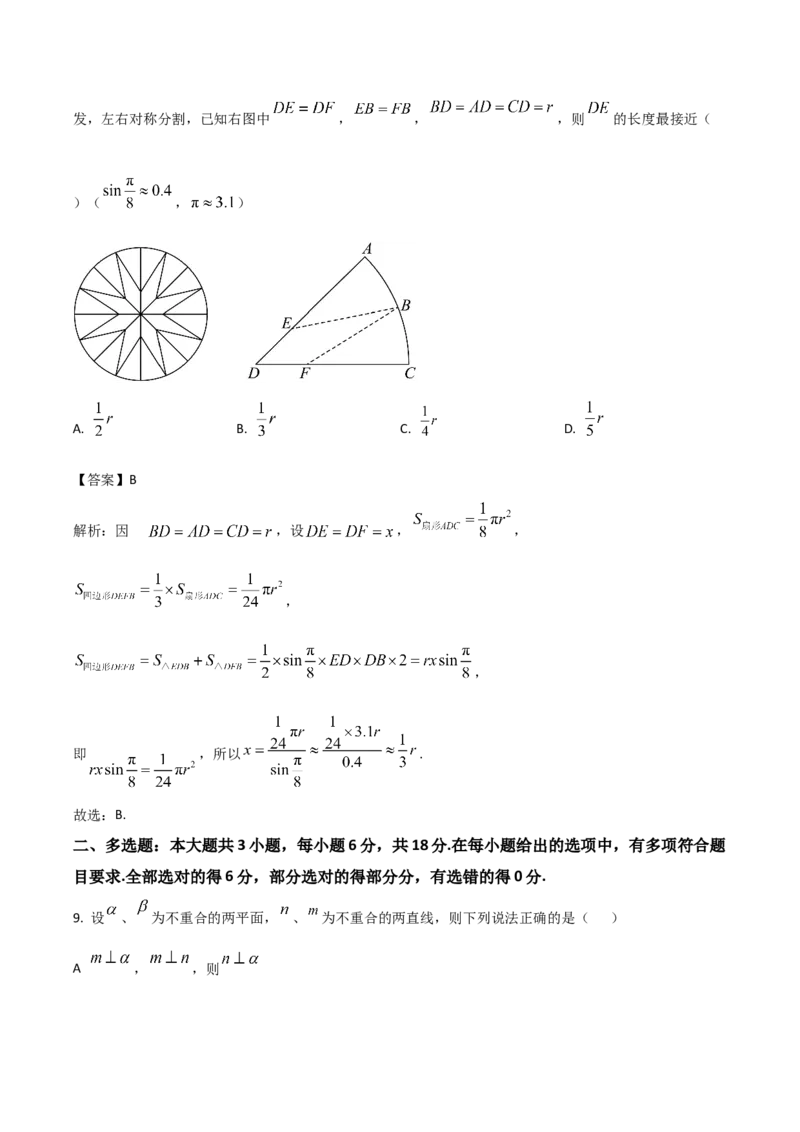
8. 某市圆形花圃,现要均分成 块,种植 种不同花卉,工匠计划将花圃按左图方式分割.先将花圃均
分成 块,在按照右图将每个 角花圃近似的均分成三块(三部分面积近似均等),从弧 的中点 出发,左右对称分割,已知右图中 , , ,则 的长度最接近(
)( , )
A. B. C. D.
【答案】B
解析:因 为,设 , ,
,
,
即 ,所以 .
故选:B.
二、多选题:本大题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题
目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.
9. 设 、 为不重合的两平面, 、 为不重合的两直线,则下列说法正确的是( )
A , ,则B. , , , , ,则
C , ,则
D. , ,则
【答案】BD
解析:对于A选项,若 , ,则 或 ,A错;
对于B选项,若 , , , , ,则 ,B对;
对于C选项,若 , ,则 或 ,C错;
对于D选项,若 , ,由线面垂直的性质可得 ,D对.
故选:BD.
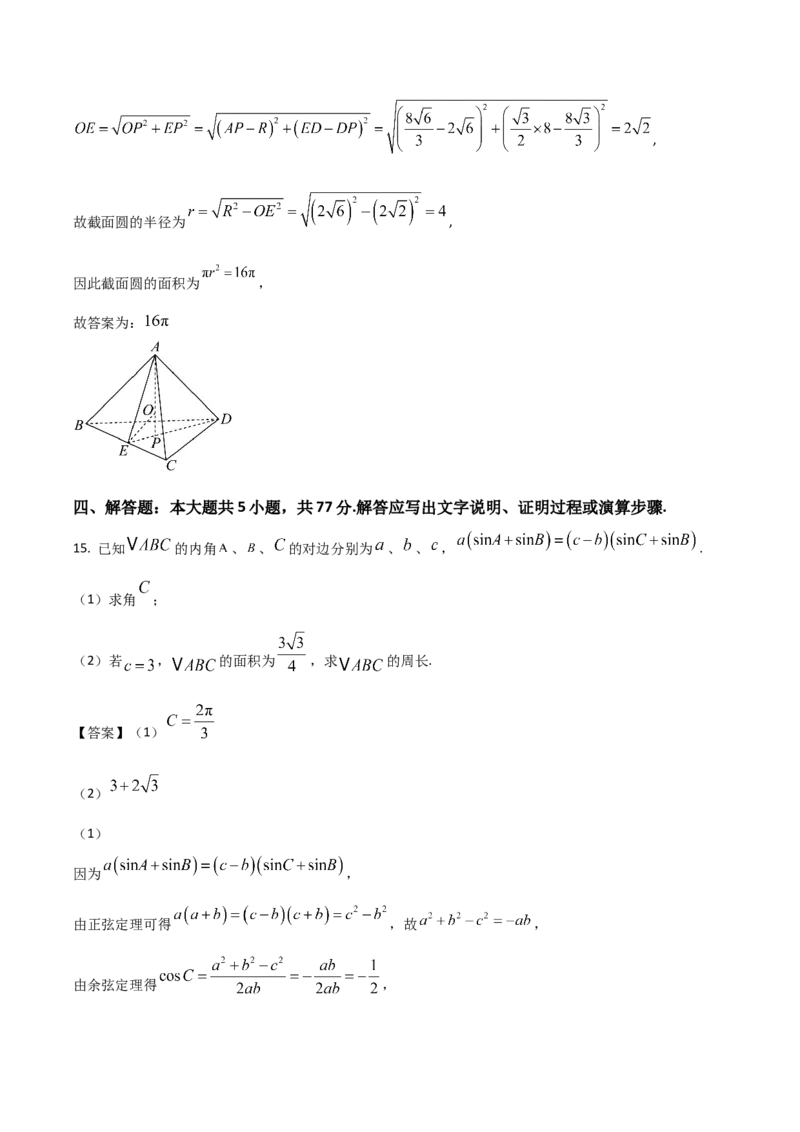
10. 已知复数 , 则下列说法正确的是( )
A. B. 对应的点在复平面的第三象限
C. ,则 为实数 D. ,则 为纯虚数
【答案】ACD
解析:对于A, ,故A正确,
对于B, ,则对应的点为 ,位于第二象限,故B错误,
对于C, 为实数,故C正确,
对于D, 为纯虚数,故D正确,
故选:ACD
11. 在日常生活中,向量无处不在,如图所示的情境,两个人共提一个行李包.假设行李包所受重力为 ,作用在行李包上的两个拉力分别为 , ,且 , 与 的夹角为 .给出以下结论,
其中正确的是( )
A. 越大越费力, 越小越省力 B. 当 时,
C. 当 时, D. 当 时,
【答案】AD
解析:对于A,由 为定值,
所以 ,
解得 ;
由题意知 时, 单调递减,且 为定值,由符合函数的单调性可得 单调递增,
即 越大越费力, 越小越省力,故A正确;
对于B,当 时, ,故B错误
对于C,当 时, ,所以 ,故C错误;
对于D,当 时, ,所以 ,故D正确.
故选:AD.三、填空题:本大题共3小题,每小题5分,共15分.
12. 已知向量 , ,若 ,则 _____.
【答案】
解析:因为向量 , ,且 ,则 ,解得 .
故答案为: .
13. 是关于 的方程 的一个根,则实数 __________.
【答案】10
解析:若一元二次方程存在虚数根,则该方程的两个根为共轭复数,
即 为该方程的两根,由韦达定理, .
故答案为:10.
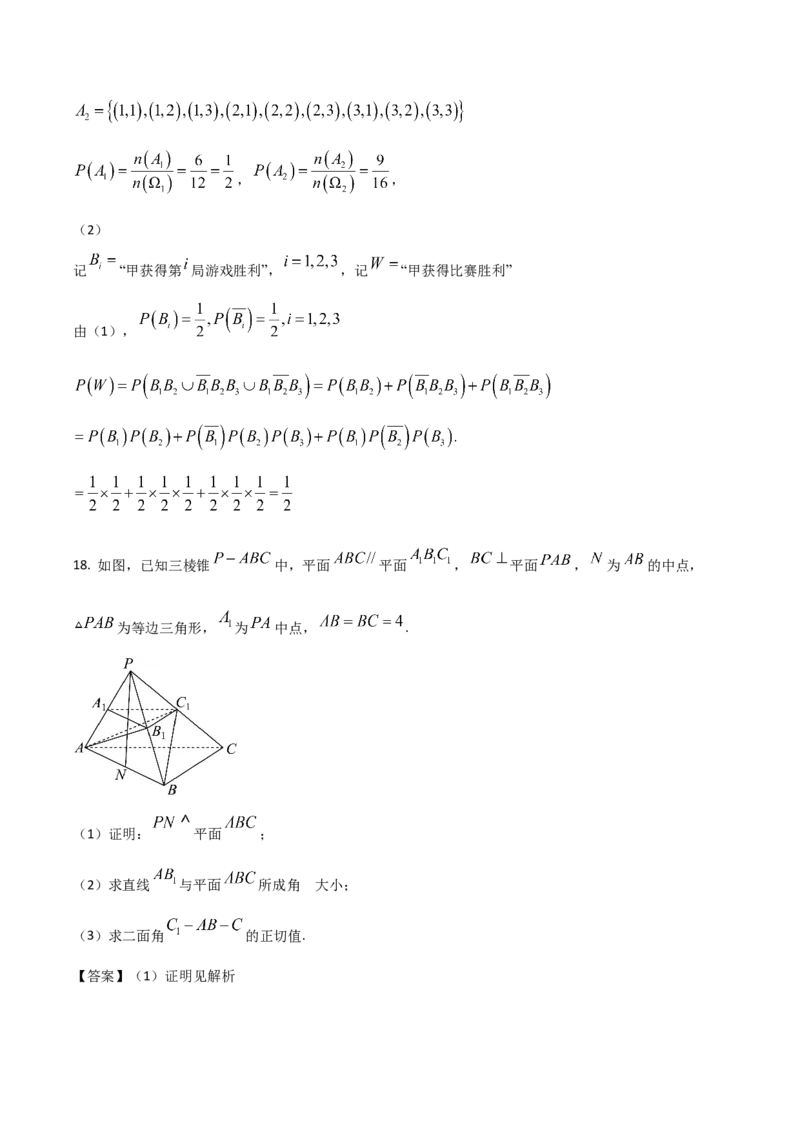
14. 正四面体 的棱长为8, 为棱 的中点,过点 作正四面体 外接球的截面,则截面
面积的最小值为_____.
【答案】
解析:由正四面体的特征可知其外接球的球心在高 所在的直线上,设球心为 ,
则 , ,
,
设外接球的半径为 ,则 ,
代入 的值可得 ,
要使过点 作正四面体 外接球的截面中面积最小,则 到球心的距离最大,即 与截面垂直时,
此时截面最小,
则 到球心的距离,
故截面圆的半径为 ,
因此截面圆的面积为 ,
故答案为:
四、解答题:本大题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.
15. 已知 的内角 、 、 的对边分别为 、 、 , .
(1)求角 ;
(2)若 , 的面积为 ,求 的周长.
【答案】(1)
(2)
(1)
因为 ,
由正弦定理可得 ,故 ,
由余弦定理得 ,因为 ,故 .
(2)
由三角形的面积公式得 ,可得 ,
由余弦定理得 ,
解得 ,故 的周长为 .
16. 2025年NBA选秀大会,我国选手杨瀚森将参加选秀,为备战选秀,运动员参加了联合试训,其中甲、
乙两位运动员开展了队内三分投篮对抗赛.在对抗赛中两人每轮投篮10次,共进行10轮,每轮命中的成绩
(个数)如下:
甲 4 7 6 5 4 9 10 7 8 10
乙 7 5 8 6 7 9 7 6 7 8
(1)求甲运动员的样本数据第75百分位数;
(2)分别计算这两位运动员10轮投篮成绩的平均数和方差;
(3)根据第二问结果回答下列问题:甲、乙两位运动员谁的发挥更稳定,为什么?
【答案】(1)9 (2)甲的平均数为7,方差为4.6,乙的平均数为7,方差为1.2
(3)乙发挥的更加稳定,理由见解析
(1)
甲运动员的成绩从小到大排列为 ,
,故甲运动员的样本数据第75百分位数为9,
(2)
甲的平均数为 ,
方差为
乙的平均数为方差为
(3)
由(2)知: ,
故乙发挥的更加稳定.
17. 一个不透明的袋中装有除了颜色外大小、质地均一致的4个小球,其中3个红球,1个白球,设计了两
个摸球游戏,其规则如下表所示:
游戏1 游戏2
摸球方式 不放回依次摸2球 有放回依次摸2球
获胜规则 若摸出2个红球,则甲获胜,否则乙获胜
(1)写出游戏1与游戏2的样本空间,并分别求出在游戏1与游戏2中甲获胜的概率;
(2)甲与乙两人玩游戏1,约定每局胜利的人得2分,否则得0分,先得到4分的人获得比赛胜利,则游
戏结束.每局游戏结果互不影响,求甲获得比赛胜利的概率.
【答案】(1) , ,
(2)
(1)
记三个红球为 号,记白球为 号,用 表示两次摸球的情况,
记游戏1与游戏2的样本空间分别为 ,
记 “在游戏1中甲获胜”,记 “在游戏2中甲获胜”, ,
(2)
记 “甲获得第 局游戏胜利”, ,记 “甲获得比赛胜利”
由(1),
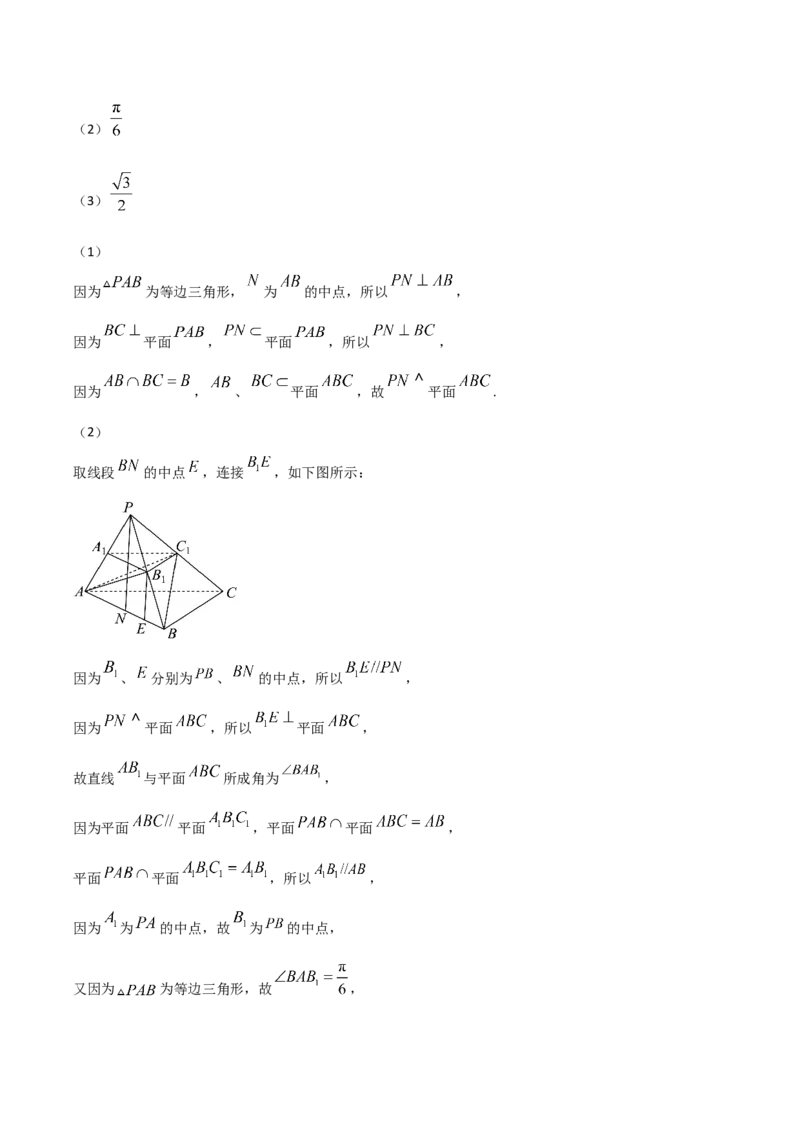
18. 如图,已知三棱锥 中,平面 平面 , 平面 , 为 的中点,
为等边三角形, 为 中点, .
(1)证明: 平面 ;
的
(2)求直线 与平面 所成角 大小;
(3)求二面角 的正切值.
【答案】(1)证明见解析(2)
(3)
(1)
因为 为等边三角形, 为 的中点,所以 ,
因为 平面 , 平面 ,所以 ,
因为 , 、 平面 ,故 平面 .
(2)
取线段 的中点 ,连接 ,如下图所示:
因为 、 分别为 、 的中点,所以 ,
因为 平面 ,所以 平面 ,
故直线 与平面 所成角为 ,
因为平面 平面 ,平面 平面 ,
平面 平面 ,所以 ,
因为 为 的中点,故 为 的中点,
又因为 为等边三角形,故 ,因此,直线 与平面 所成角为 .
(3)
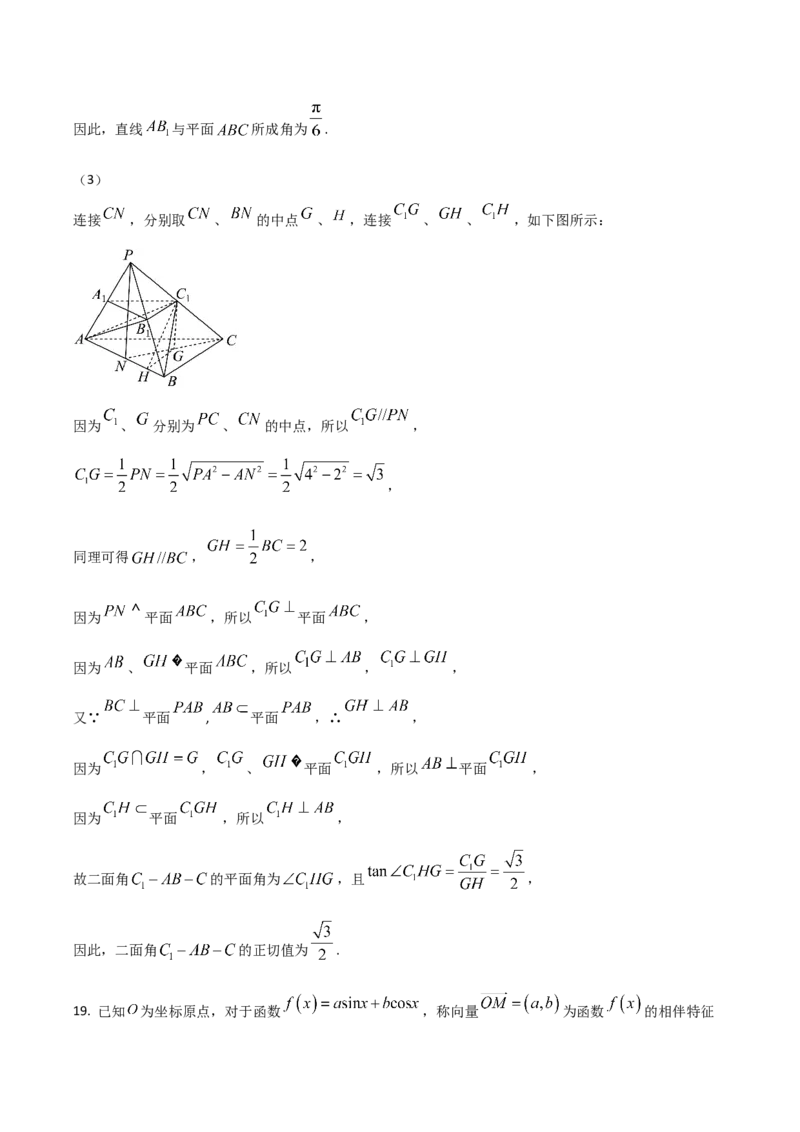
连接 ,分别取 、 的中点 、 ,连接 、 、 ,如下图所示:
因为 、 分别为 、 的中点,所以 ,
,
同理可得 , ,
因为 平面 ,所以 平面 ,
因为 、 平面 ,所以 , ,
又∵ 平面 , 平面 ,∴ ,
因为 , 、 平面 ,所以 平面 ,
因为 平面 ,所以 ,
故二面角 的平面角为 ,且 ,
因此,二面角 的正切值为 .
19. 已知 为坐标原点,对于函数 ,称向量 为函数 的相伴特征向量,同时称函数 为向量 的相伴函数.
(1)记向量 的相伴函数为 ,若当 且 时,求 的值;
(2)设 ,试求函数 的相伴特征向量 ,并求出与
同向的单位向量;
(3)已知 为函数 的相伴特征向量,若在 中, , ,若点
为该 的外心,求 的最大值.
【答案】(1)
(2) ,
(3)
(1)
根据题意知,向量 的相伴函数为 ,
当 时, ,
又 ,则 ,所以 ,故 .
(2)
因为 ,
整理得到 ,故函数 的相伴特征向量 ,则与 同向的单位向量为 .
(3)
由题意得, ,
在 中, , ,又 ,因此 ,
设 外接圆半径为 ,根据正弦定理, ,故 ,
所以 ,
,
,
代入可得 ,
所以当 时, 取得最大值 .