文档内容
新乡市 2023-2024 学年高一期末(下) 测试
数 学
注意事项:
1. 答题前, 考生务必将自己的姓名、考生号、考场号、座位号填写在答题卡上。
2. 回答选择题时, 选出每小题答案后, 用铅笔把答题卡上对应题目的答案标号涂黑。如需改动,
用橡皮擦干净后, 再选涂其他答案标号。回答非选择题时, 将答案写在答题卡上。写在本试卷上
无效。
3. 考试结束后, 将本试卷和答题卡一并交回。
4. 本试卷主要考试内容: 人教 A 版必修第一册占 25% ,第二册占 75% 。
一、选择题: 本题共 8 小题, 每小题 5 分, 共 40 分. 在每小题给出的四个选项中, 只有一项是
符合题目要求的.
1. 已知集合 A={x∈Z∣−2x<−1},B={x∣x2−x−2≤0} ,则 A∩B=( )
A. {1} B. {−1,0} C. {1,2} D. {−1,0,1,2}
2−2i
2. =( )
3i+4
1 7 2 14 2 14
A. − i B. − i C. + i D.
13 13 25 25 25 25
1 7
− + i
25 25
x2−1
3. 已知函数 f (x)= 是奇函数,则 a=( )
x+a
A. 0 B. -1 D. 2
4. 已知平面向量 a,b 满足 |a|=1,|b|=2 ,且 |2a−b|=√7 ,则 cos⟨a,b⟩=( )
1 1 1 1
A. B. C. D.
2 4 6 8
( π)
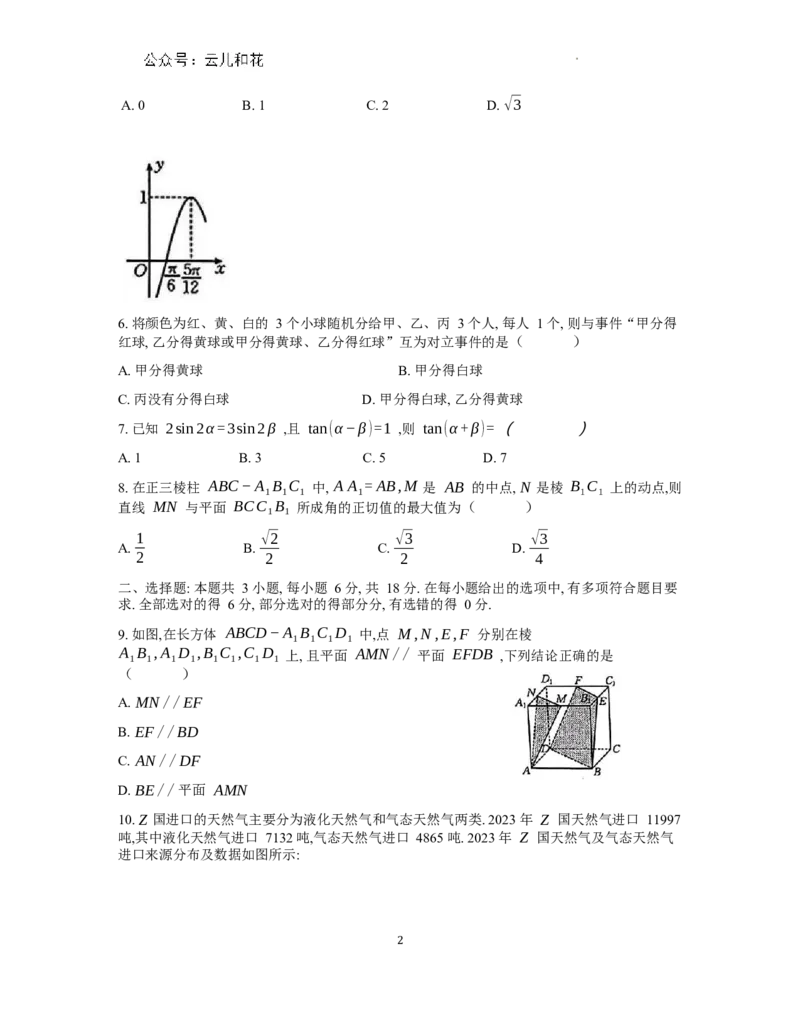
5. 已知函数 f (x)=sin(ωx+φ) ω>0,|φ|≤ 的部分图象如图所示,则
2
(8π)
f =( )
3
1
学科网(北京)股份有限公司A. 0 B. 1 C. 2 D. √3
6. 将颜色为红、黄、白的 3 个小球随机分给甲、乙、丙 3 个人, 每人 1 个, 则与事件“甲分得
红球, 乙分得黄球或甲分得黄球、乙分得红球”互为对立事件的是( )
A. 甲分得黄球 B. 甲分得白球
C. 丙没有分得白球 D. 甲分得白球, 乙分得黄球
7. 已知 2sin2α=3sin2β ,且 tan(α−β)=1 ,则 tan(α+β)=( )
A. 1 B. 3 C. 5 D. 7
8. 在正三棱柱 ABC−A B C 中, A A =AB,M 是 AB 的中点, N 是棱 B C 上的动点,则
1 1 1 1 1 1
直线 MN 与平面 BCC B 所成角的正切值的最大值为( )
1 1
1 √2 √3 √3
A. B. C. D.
2 2 2 4
二、选择题: 本题共 3 小题, 每小题 6 分, 共 18 分. 在每小题给出的选项中, 有多项符合题目要
求. 全部选对的得 6 分, 部分选对的得部分分, 有选错的得 0 分.
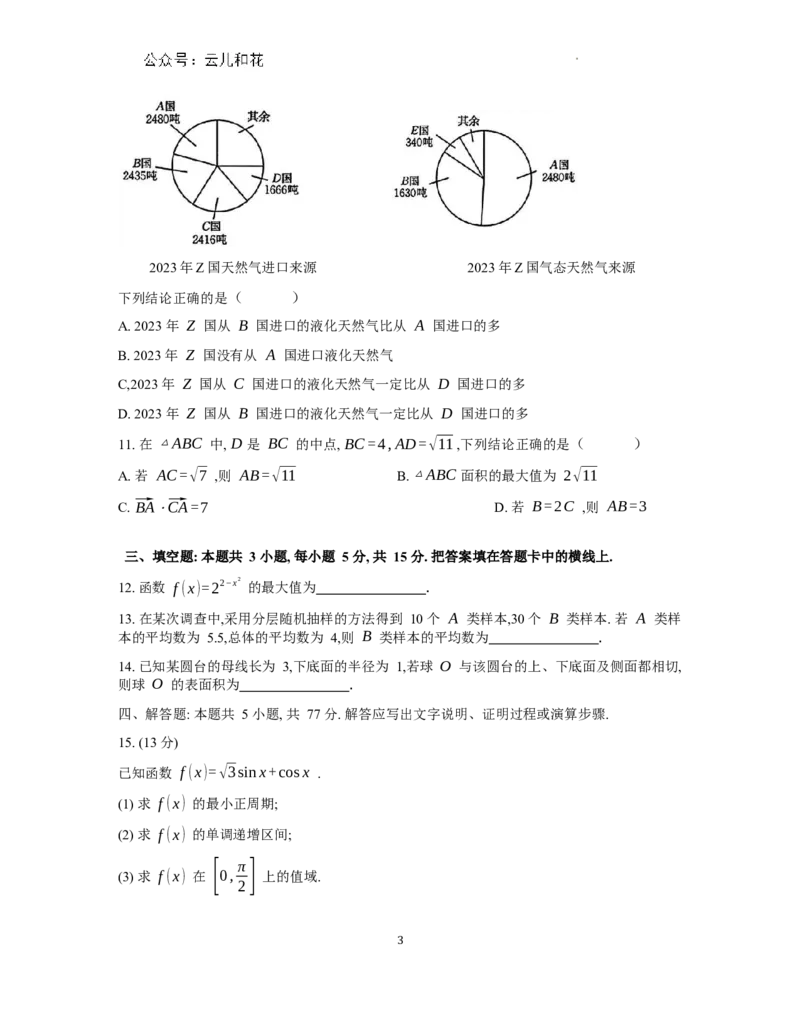
9. 如图,在长方体 ABCD−A B C D 中,点 M,N,E,F 分别在棱
1 1 1 1
A B ,A D ,B C ,C D 上, 且平面 AMN// 平面 EFDB ,下列结论正确的是
1 1 1 1 1 1 1 1
( )
A. MN//EF
B. EF//BD
C. AN//DF
D. BE// 平面 AMN
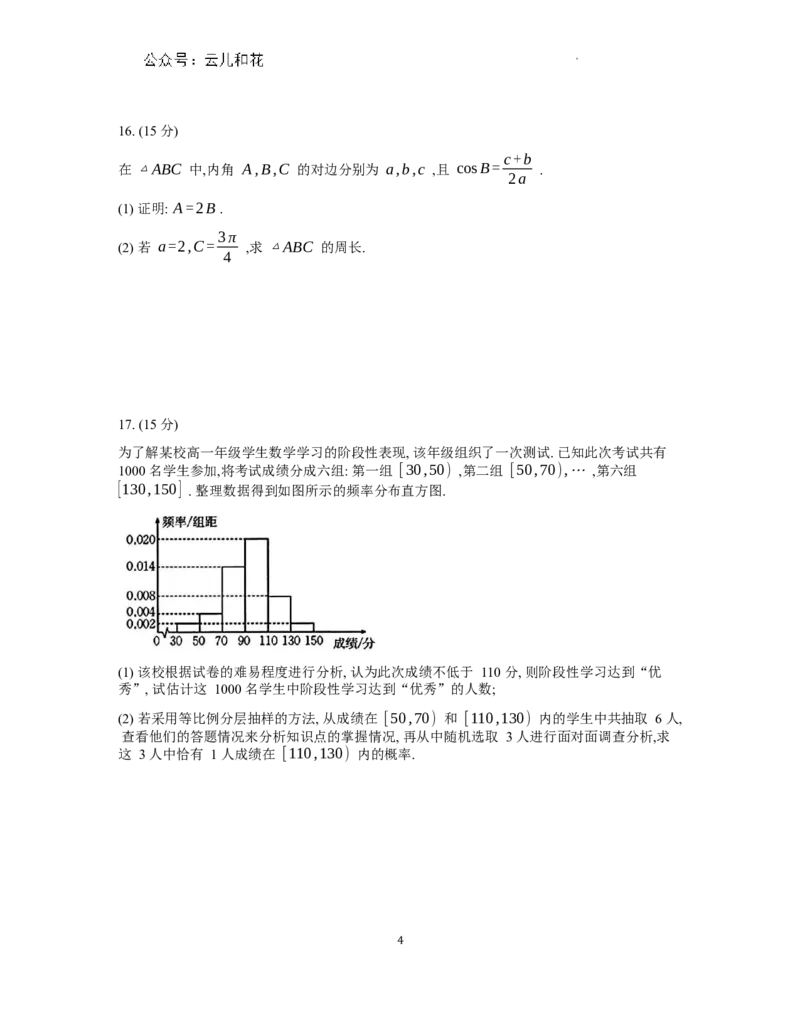
10. Z 国进口的天然气主要分为液化天然气和气态天然气两类. 2023 年 Z 国天然气进口 11997
吨,其中液化天然气进口 7132 吨,气态天然气进口 4865 吨. 2023 年 Z 国天然气及气态天然气
进口来源分布及数据如图所示:
2
学科网(北京)股份有限公司2023年Z国天然气进口来源 2023年Z国气态天然气来源
下列结论正确的是( )
A. 2023 年 Z 国从 B 国进口的液化天然气比从 A 国进口的多
B. 2023 年 Z 国没有从 A 国进口液化天然气
C,2023 年 Z 国从 C 国进口的液化天然气一定比从 D 国进口的多
D. 2023 年 Z 国从 B 国进口的液化天然气一定比从 D 国进口的多
11. 在 △ABC 中, D 是 BC 的中点, BC=4,AD=√11 ,下列结论正确的是( )
A. 若 AC=√7 ,则 AB=√11 B. △ABC 面积的最大值为 2√11
C. ⃗BA⋅⃗CA=7 D. 若 B=2C ,则 AB=3
三、填空题: 本题共 3 小题, 每小题 5 分, 共 15 分. 把答案填在答题卡中的横线上.
12. 函数 f (x)=22−x2 的最大值为 .
13. 在某次调查中,采用分层随机抽样的方法得到 10 个 A 类样本,30 个 B 类样本. 若 A 类样
本的平均数为 5.5,总体的平均数为 4,则 B 类样本的平均数为 .
14. 已知某圆台的母线长为 3,下底面的半径为 1,若球 O 与该圆台的上、下底面及侧面都相切,
则球 O 的表面积为 .
四、解答题: 本题共 5 小题, 共 77 分. 解答应写出文字说明、证明过程或演算步骤.
15. (13 分)
已知函数 f (x)=√3sinx+cosx .
(1) 求 f (x) 的最小正周期;
(2) 求 f (x) 的单调递增区间;
[ π]
(3) 求 f (x) 在 0, 上的值域.
2
3
学科网(北京)股份有限公司16. (15 分)
c+b
在 △ABC 中,内角 A,B,C 的对边分别为 a,b,c ,且 cosB= .
2a
(1) 证明: A=2B .
3π
(2) 若 a=2,C= ,求 △ABC 的周长.
4
17. (15 分)
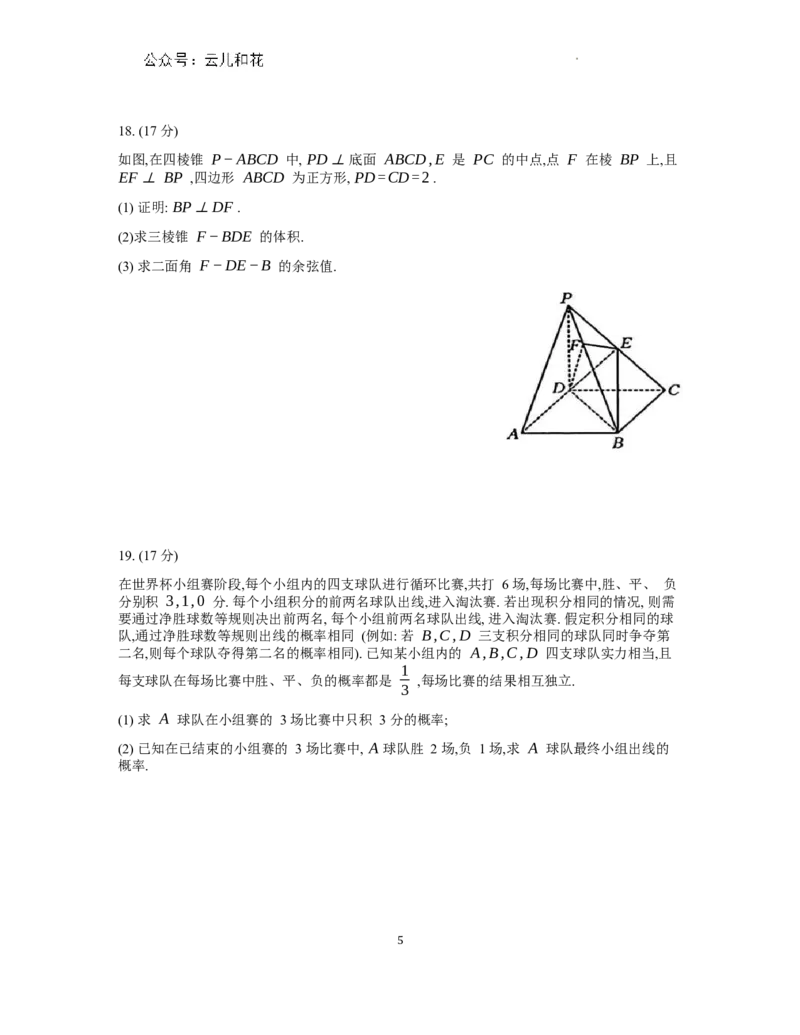
为了解某校高一年级学生数学学习的阶段性表现, 该年级组织了一次测试. 已知此次考试共有
1000 名学生参加,将考试成绩分成六组: 第一组 [30,50) ,第二组 [50,70),⋯ ,第六组
[130,150] . 整理数据得到如图所示的频率分布直方图.
(1) 该校根据试卷的难易程度进行分析, 认为此次成绩不低于 110 分, 则阶段性学习达到“优
秀”, 试估计这 1000 名学生中阶段性学习达到“优秀”的人数;
(2) 若采用等比例分层抽样的方法, 从成绩在 [50,70) 和 [110,130) 内的学生中共抽取 6 人,
查看他们的答题情况来分析知识点的掌握情况, 再从中随机选取 3 人进行面对面调查分析,求
这 3 人中恰有 1 人成绩在 [110,130) 内的概率.
4
学科网(北京)股份有限公司18. (17 分)
如图,在四棱锥 P−ABCD 中, PD⊥ 底面 ABCD,E 是 PC 的中点,点 F 在棱 BP 上,且
EF⊥ BP ,四边形 ABCD 为正方形, PD=CD=2 .
(1) 证明: BP⊥DF .
(2)求三棱锥 F−BDE 的体积.
(3) 求二面角 F−DE−B 的余弦值.
19. (17 分)
在世界杯小组赛阶段,每个小组内的四支球队进行循环比赛,共打 6 场,每场比赛中,胜、平、 负
分别积 3,1,0 分. 每个小组积分的前两名球队出线,进入淘汰赛. 若出现积分相同的情况, 则需
要通过净胜球数等规则决出前两名, 每个小组前两名球队出线, 进入淘汰赛. 假定积分相同的球
队,通过净胜球数等规则出线的概率相同 (例如: 若 B,C,D 三支积分相同的球队同时争夺第
二名,则每个球队夺得第二名的概率相同). 已知某小组内的 A,B,C,D 四支球队实力相当,且
1
每支球队在每场比赛中胜、平、负的概率都是 ,每场比赛的结果相互独立.
3
(1) 求 A 球队在小组赛的 3 场比赛中只积 3 分的概率;
(2) 已知在已结束的小组赛的 3 场比赛中, A 球队胜 2 场,负 1 场,求 A 球队最终小组出线的
概率.
5
学科网(北京)股份有限公司