文档内容
2024 学年第一学期高一年级 10 月四校联考
数学学科试题卷
命题人:浦江中学 徐德荣 校对人:浦江中学 于杭君
考生须知:
1.本卷满分 150分,考试时间 120分钟;
2.答题前,在答题卷指定区域填写班级、姓名、考场、座位号及准考证号(填涂);
3.所有答案必须写在答题卷上,写在试卷上无效;
一、选择题:本题共 8小题,每小题 5分,共 40分.在每小题给出的四个选项中,只有一项是
符合题目要求的.
1.已知集合A={ 1,2,3,4,5,9 } ,B= { x∣ x∈A } ,则 ( A∩B )=( )
A
{ } { } { } { }
A. 2,3,5 B. 3,4,9 C. 1,4,9 D. 1,2,3
2.如图,已知全集U =R,集合A={ 1,2,3,4,5 } ,B={ x∣−1≤ x≤2 } ,则图中阴影部分表示的集合的子集
个数为( )
A.3 B.4 C.7 D.8
3.已知x,y∈R,则“xy =0”是“x2 + y2 =0”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
4.已知a+b>0,a<0,那么a,b,−a,−b的大小关系是( )
A.b>−a >−b>a B.a >−b>−a>b
C.b>−a >a >−b D.a >b>−a >−b
5.命题“∃x>0,x2 > x3”的否定是( )
A.∀x>0,x2 > x3 B.∀x>0,x2 ≤ x3
C.∀x≤0,x2 ≤ x3 D.∃x>0,x2 ≤ x3
6.若命题“∃x∈[−1,3 ] ,x2 −2x−a≤0”为真命题,则实数a可取的最小整数值是( )
A.−1 B.0 C.1 D.3
学科网(北京)股份有限公司( x−2 )( ax+b )
7.已知关于x不等式 ≥0的解集为 (−∞,−2 ]∪( 1,2 ] ,则( )
x−c
A.c=2
( )
B.点 a,b 在第二象限
C.y =ax2 +bx−2a的最大值为3a
D.关于x的不等式ax2 +ax−b≥0的解集为 [−2,1 ]
8.若数集A={ a ,a ,,a }( 1≤a 20.
11.若正实数x,y满足2x+ y =1,则下列说法正确的是( )
学科网(北京)股份有限公司1
A.xy有最大值为
8
1 4
B. + 有最小值为6+4 2
x y
1
C.4x2 + y2有最小值为
2
1
D.x ( y+1 ) 有最大值为
2
三、填空题:本题共 3小题,每小题 5分,共 15分.
12.某学校举办秋季运动会时,高一某班共有24名同学参加比赛,有12人参加游泳比赛,有9人参加田
赛,有13人参加径赛,同时参加游泳比赛和田赛的有3人,同时参加游泳比赛和径赛的有3人,没有人
同时参加三项比赛,借助韦恩图,可知同时参加田赛和径赛的有__________人.
13.甲、乙两地相距1000千米,汽车从甲地匀速行驶到乙地,已知汽车每小时的运输成本(以元为单位)由
可变部分和固定部分组成.可变部分与速度x(千米/时)的平方成正比,比例系数为2,固定部分为5000
元.为使全程运输成本最小,汽车的速度是__________千米/时.
1
14.若一个三角形的三边长分别为a,b,c,记 p= ( a+b+c ),则此三角形面积
2
S = p ( p−a )( p−b )( p−c ) ,这是著名的海伦公式.已知ABC的周长为9,c=2,则ABC的面积的
最大值为__________.
四、解答题:本题共 5小题,共 77分.解答题应写出文字说明、证明过程或演算步骤.
15.(本题满分13分)用篱笆在一块靠墙的空地围一个面积为75 3m2的等腰梯形菜园,如图所示,用墙
的一部分做下底AD,用篱笆做两腰及上底,且腰与墙成60,当等腰梯形的腰长为多少时,所用篱笆的
长度最小?并求出所用篱笆长度的最小值.
16.(本题满分15分)已知集合A={ x∣−2≤ x−1≤5 } 、集合B={ x∣m+1≤ x≤2m−1 }( m∈R ) .
(1)若m=4,求 ( A∪B ) ;
R
(2)设命题 p:x∈A;命题q:x∈B,若命题 p是命题q的必要不充分条件,求实数m的取值范围
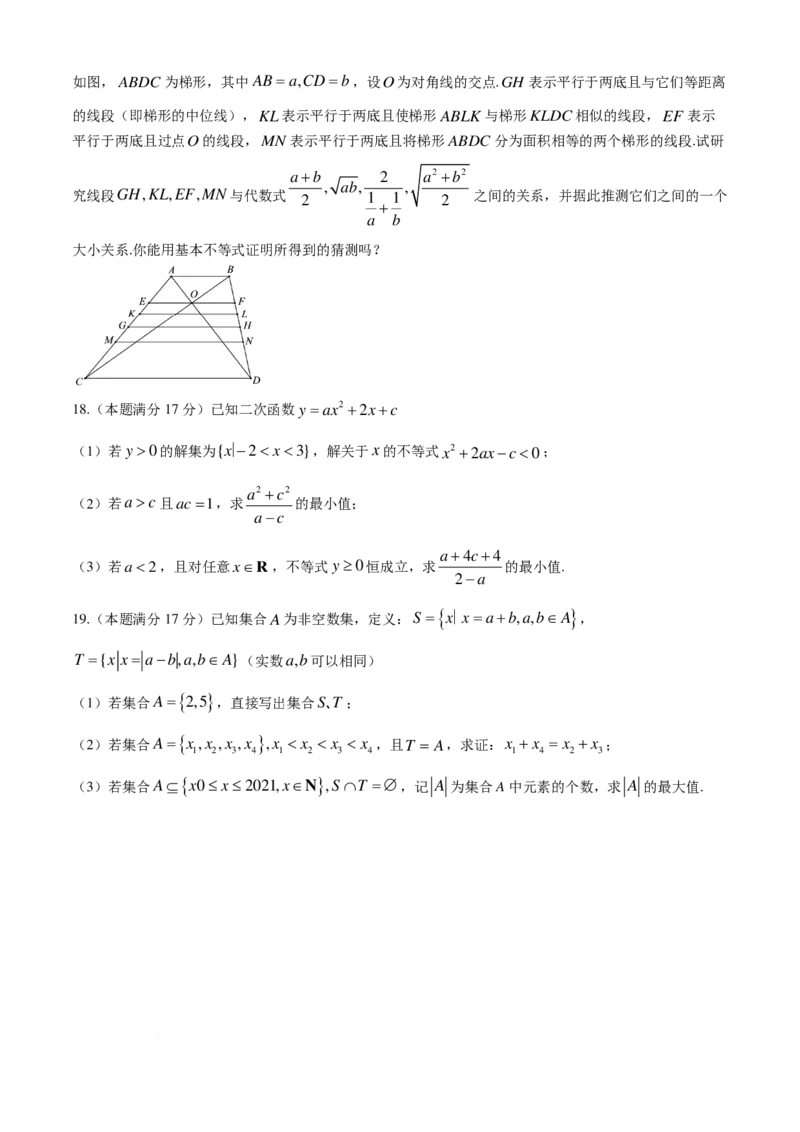
17.(本题满分15分)
学科网(北京)股份有限公司如图,ABDC为梯形,其中AB=a,CD=b,设O为对角线的交点.GH 表示平行于两底且与它们等距离
的线段(即梯形的中位线),KL表示平行于两底且使梯形ABLK与梯形KLDC相似的线段,EF 表示
平行于两底且过点O的线段,MN 表示平行于两底且将梯形ABDC分为面积相等的两个梯形的线段.试研
a+b 2 a2 +b2
, ab, ,
究线段GH,KL,EF,MN与代数式 2 1 1 2 之间的关系,并据此推测它们之间的一个
+
a b
大小关系.你能用基本不等式证明所得到的猜测吗?
18.(本题满分17分)已知二次函数y =ax2 +2x+c
(1)若y >0的解集为{x∣−2< x<3},解关于x的不等式x2 +2ax−c<0;
a2 +c2
(2)若a>c且ac=1,求 的最小值;
a−c
a+4c+4
(3)若a<2,且对任意x∈R,不等式y≥0恒成立,求 的最小值.
2−a
19.(本题满分17分)已知集合A为非空数集,定义:S ={ x∣x=a+b,a,b∈A } ,
T ={x x= a−b|,a,b∈A}(实数a,b可以相同)
(1)若集合A={ 2,5 } ,直接写出集合S、T ;
(2)若集合A={ x ,x ,x ,x } ,x < x < x < x ,且T = A,求证:x +x = x +x ;
1 2 3 4 1 2 3 4 1 4 2 3
(3)若集合A⊆{ x0≤ x≤2021,x∈N } ,S∩T =∅,记 A 为集合A中元素的个数,求 A 的最大值.
学科网(北京)股份有限公司2024 学年第一学期高一年级 10 月四校联考
数学学科参考答案
一、选择题:本题共 8小题,每小题 5分,共 40分.在每小题给出的四个选项中,只有一项是
符合题目要求的.
1 2 3 4 5 6 7 8
A D B C B A D B
二、多选题:本题 3小题,每小题 6分,共 18分.在每小题给出的选项中,有多项符合题目要
求全部选对得 6分,部分选对得部分分,有错选的得 0分.
9 10 11
AC AD ABC
3 5
12.4 13.50 14.
2
9
14.由海伦公式及基本不等式求解即: p = ,c= AB =2,则a+b=周长−c=9−2=7,
2
故( p−a )+( p−b )=2p−( a+b )=9−7=2;S = p ( p−a )( p−b )( p−c )
9 9
−a +
−b
99 9 9 459 9 3 5 2 2 3
= −a −b −2 = −a −b ≤ ⋅ = 5.
22 2 2 4 2 2 2 2 2
9 9 7 3
等号成立时, −a = −b,即a =b= ,故答案为: 5
2 2 2 2
15.设AB=a ( m )( a>0 ) ,上底BC =b ( m )( b>0 ) ,
学科网(北京)股份有限公司3 a
分别过点B,C 作下底的垂线,垂足分别为E,F,则BE = a,AE = DF = ,
2 2
a a
则下底AD= +b+ =a+b,
2 2
( b+a+b ) 3 3
该等腰梯形的面积S = ⋅ a = ( a+2b ) a =75 3,
2 2 4
300 a
所以 ( a+2b ) a=300,则b= − ,所用篱笆长为
2a 2
300 a 300 3a 300 3a
l =2a+b=2a+ − = + ≥2 ⋅ =30,
2a 2 2a 2 2a 2
300 3a
当且仅当 = ,即a =10 ( m ) ,b=10 ( m ) 时取等号.
2a 2
所以,当等腰梯形的腰长为10m时,所用篱笆长度最小,其最小值为30m.
16.(1)由题意可知A={ x∣−2≤ x−1≤5 }={ x∣−1≤ x≤6 } ,
若m=4,B={ x∣5≤ x≤7 } , ( A∪B )={x∣x<−1,x>7}.
R
(2)命题 p是命题q的必要不充分条件,∴集合B是集合A.真子集,
当B=∅时,m+1>2m−1,解得m<2,
m+1≤2m−1
7
当B≠∅时,m+1≥−1 (等号不能同时成立),解得2≤m≤ ,
2
2m−1≤6
7
综上所述,实数m的取值范围为 −∞,
2
AB+CD a+b
17.因为GH 是梯形ABDC的中位线,所以GH = = ;
2 2
AB KL
因为梯形ABLK与梯形KLDC相似,所以 = ,
KL CD
所以KL= AB×CD = ab ;
学科网(北京)股份有限公司OE OA OF OD OE OF
因为AEO∽ACD,DOF∽DAB,所以 = , = ,所以 + =1,所以
b DA a AD b a
1 2
OE =OF = EF =
1 1 ,所以 1 1 ,
+ +
a b a b
设梯形MNDC,ABNMABDC的面积分别为S ,S ,S,高分别为h,h ,h,
1 2 1 2
1 1
则S =S = S, ( a+b ) h=( b+MN ) h =( a+MN ) h ,
1 2 2 2 1 2
1 1
所以 2 ( a+b ) h 2 ( a+b ) h ,所以 1 ( a+b ) 1 + 1 =1,
+ =h 2 a+MN b+MN
a+MN b+MN
a2 +b2
所以MN = ;
2
2 a+b a2 +b2
< ab < <
由图可知,EF < KL ab, < = ab
证明:显然 2 1 1 1 因为a2 +b2 >2ab,
+
2
a b ab
( ) a+b a2 +b2
所以2 a2 +b2 >(a+b)2,所以 < ,
2 2
2 a+b a2 +b2
< ab < <
所以 1 1 2 2 .
+
a b
18.(1)由已知ax2 +2x+c>0的解集为{x∣−2< x<3},且a<0,所以−2,3是方程ax2 +2x+c=0的
2 c
解,所以−2+3=− , (−2 )×3= ,所以a =−2,c=12,所以不等式x2 +2ax−c<0可化为
a a
x2 −4x−12<0,所以−2< x<6,故不等式x2 +2ax−c<0的解集为{x∣−2< x<6}
a2 +c2 (a−c)2 +2ac 2
(2)因为ac=1,所以 = =( a−c )+
a−c a−c a−c
a2 +c2 2
因为a>c,所以a−c>0,由基本不等式可得 =( a−c )+ ≥2 2,
a−c a−c
学科网(北京)股份有限公司6+ 2 6− 2
当且仅当a−c= 2,ac=1时等号成立,即当且仅当a = ,c= 时等号成立;
2 2
a2 +c2
所以 的最小值为2 2;
a−c
(3)因为对任意x∈R,不等式ax2 +2x+c≥0恒成立,
4 4c 4 4
+ +1 + +1
a+4c+4 a a a2 a
所以a >0,4−4ac≤0,所以a >0,ac≥1, = ≥ ,
2−a 2 2
−1 −1
a a
2 2 a+4c+4 (t+1)2 +2 ( t+1 )+1 4
令t = −1,则t >0, =t+1,所以 ≥ =t+4+ ≥8,
a a 2−a t t
2
当且仅当 =3,ac=1时等号成立,
a
2 3 a+4c+4
即当且仅当a= ,c= 时等号成立,所以 的最小值为8.
3 2 2−a
19.(1)因为集合A={ 2,5 } ,S ={ x∣x=a+b,a,b∈A } ,T ={x x= a−b|,a,b∈A},
所以由2+2=4,2+5=7,5+5=10,可得S ={ 4,7,10 } ,
2−2 =0, 5−5 =0, 2−5 =3,可得T ={ 0,3 } .
(2)由于集合A={ x ,x ,x ,x } ,x < x < x < x ,
1 2 3 4 1 2 3 4
则T 集合的元素在0,x −x ,x −x ,x −x ,x −x ,x −x ,x −x 中,
2 1 3 1 4 1 3 2 4 2 4 3
且0< x −x < x −x < x −x ,x −x < x −x < x −x ,而A=T ,故A中最大元素x 必在T 中,
2 1 3 1 4 1 4 3 4 2 4 1 4
而x −x 为7个元素中的最大者,故x = x −x 即x =0,故A={ 0,x ,x ,x } ,
4 1 4 4 1 1 2 3 4
故T 中的4个元素为0,x ,x ,x ,
2 3 4
且x −x ,x −x ,x −x 与x ,x ,x 重复,而0< x −x < x ,故x −x = x 即x =2x ,
3 2 4 2 4 3 2 3 4 3 2 3 3 2 2 3 2
而0< x −x < x ,故0< x −x < x ,故x −x = x 或x −x = x ,
4 3 4 4 3 4 4 3 2 4 3 3
若x =2x =4x ,则A={ 0,x ,2x ,4x } ,4x −x =3x ∉T ,与题设矛盾;
4 3 2 2 2 2 2 2 2
故x −x = x 即x +x = x +x
4 3 2 4 1 3 2
学科网(北京)股份有限公司(3)设A={ a ,a ,a } 满足题意,其中a 673 ,故m的最小值为674,于是当
3
m=674时,A中元素最多,即A={ 674,675,676,,2021 } 时满足题意,综上所述,集合A中元素的
个数的最大值是1348.
学科网(北京)股份有限公司