数学-重庆七校2024年高一上学期第一次联考_2024-2025高一（7-7月题库）_2024年10月试卷_1023重庆七校2024年高一上学期第一次联考

2024—2025 学年度上期高一七校第一次联考 数学试题 满分：150分，考试时间：120分钟。 注意事项： 1．答题前，务必将自己的姓名、准考证号等填写在答题卡规定的位置上。 2．答选择题时，必须使用 2B铅笔将答题卡上对应题目的答案标号涂黑。 3．答非选择题时，必须使用 0.5毫米黑色签字笔，将答案书写在答题卡规定的位置上。 4．考试结束后，将答题卷交回。  b 4ac−b2  5．参考公式：二次函数y =ax2 +bx+c ( a≠0 )的图象的顶点坐标是 − , .  2a 4a  一、选择题（本题有 10小题，每小题 4分，共 40分，每小题只有一个选项是正确的，不选， 多选，错选，均不给分） 1．下列各数中最小的数是（ ） A．−π B．− 2 C．0 D．−3 2．下面四个图形分别是节能、节水、低碳和绿色食品标志，是轴对称图形的是（ ） A． B． C． D． 8 3．反比例函数y =− 的图象一定经过的点是（ ） x A．(−1,−8 ) B．( 2,4 ) C．(−4,2 ) D．（8，1） 4．如图，直线a//b，点B在直线a上，AB⊥ BC，若∠1=40，则∠2的度数为（ ） A．40 B．50 C．80 D．140 5．若两个相似三角形的相似比为2:3，则这两个三角形面积的比是（ ） A．2:3 B．2:5 C．4:6 D．4:9  4  6．估计 +2 3× 5的值应在（ ）    5  A．8和9之间 B．9和10之间 C．10和11之间 D．1和12之间 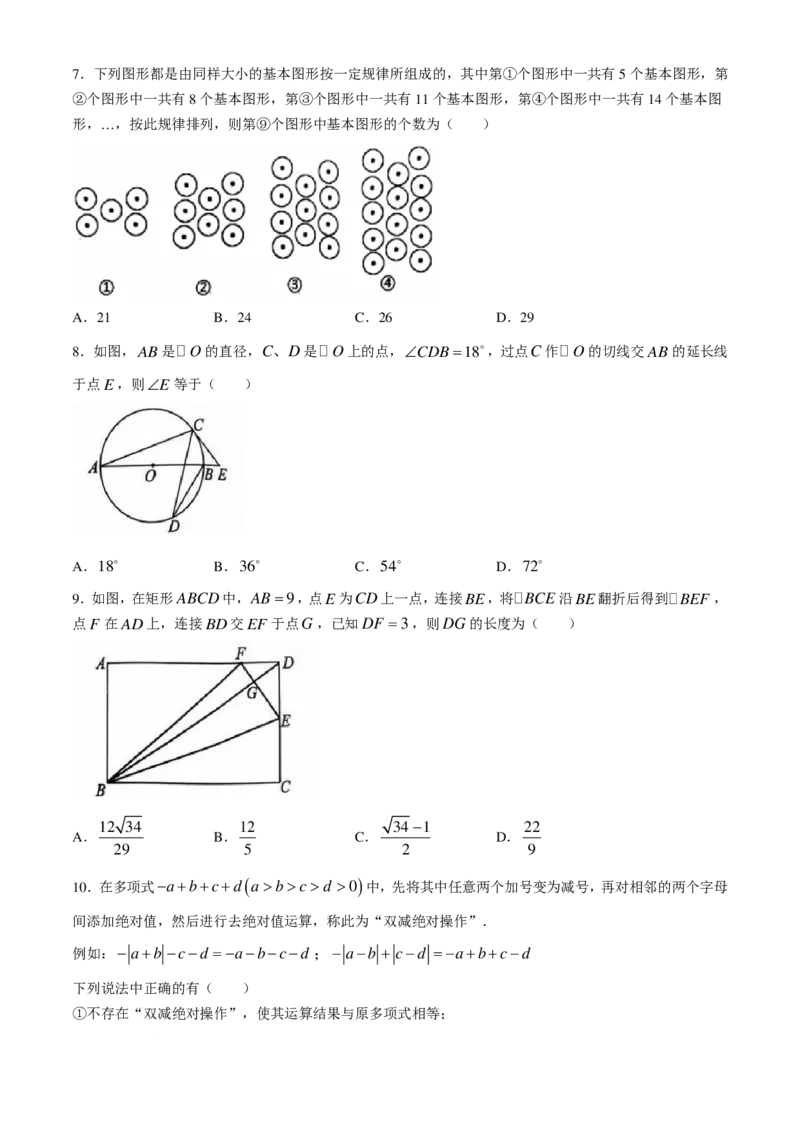学科网（北京）股份有限公司7．下列图形都是由同样大小的基本图形按一定规律所组成的，其中第①个图形中一共有5个基本图形，第 ②个图形中一共有8个基本图形，第③个图形中一共有11个基本图形，第④个图形中一共有14个基本图 形，…，按此规律排列，则第⑨个图形中基本图形的个数为（ ） A．21 B．24 C．26 D．29 8．如图，AB是 O的直径，C、D是 O上的点，∠CDB=18，过点C作 O的切线交AB的延长线 于点E，则∠E等于（ ） A．18 B．36 C．54 D．72 9．如图，在矩形ABCD中，AB=9，点E为CD上一点，连接BE，将BCE沿BE翻折后得到BEF ， 点F 在AD上，连接BD交EF 于点G，已知DF =3，则DG的长度为（ ） 12 34 12 34−1 22 A． B． C． D． 29 5 2 9 10．在多项式−a+b+c+d ( a>b>c>d >0 )中，先将其中任意两个加号变为减号，再对相邻的两个字母 间添加绝对值，然后进行去绝对值运算，称此为“双减绝对操作”． 例如：− a+b −c−d =−a−b−c−d ；− a−b + c−d =−a+b+c−d 下列说法中正确的有（ ） ①不存在“双减绝对操作”，使其运算结果与原多项式相等； 学科网（北京）股份有限公司②不存在“双减绝对操作”，使其运算结果与原多项式之和为0； ③所有的“双减绝对操作”共有7种不同的结果 A．0个 B．1个 C．2个 D．3个 二、填空题：（本大题共 8个小题，每小题 4分，共 32分）在每个小题中，请将正确答案书 写在答 ． 题 ． 卡 ． （ ． 卷 ． ）中对应的位置上． 1 11．计算： − +2−1 =______． 2 12．某校开展读书日活动，小渝和小津分别从校图书馆的“社会科学”、“自然科学”、“文学”、“艺 术”四类书籍中随机地抽取一本，抽到同一类书籍的概率是______． 13．若一个多边形的每个外角都等于60，则它的内角和等于______． 14．随着新冠疫情趋于缓和，口罩市场趋于饱和，某N95口罩每盒原价为200元，连续两次降价后每盒的 售价为72元，设每次下降的平均下降率为x，根据题意，可列方程为______． 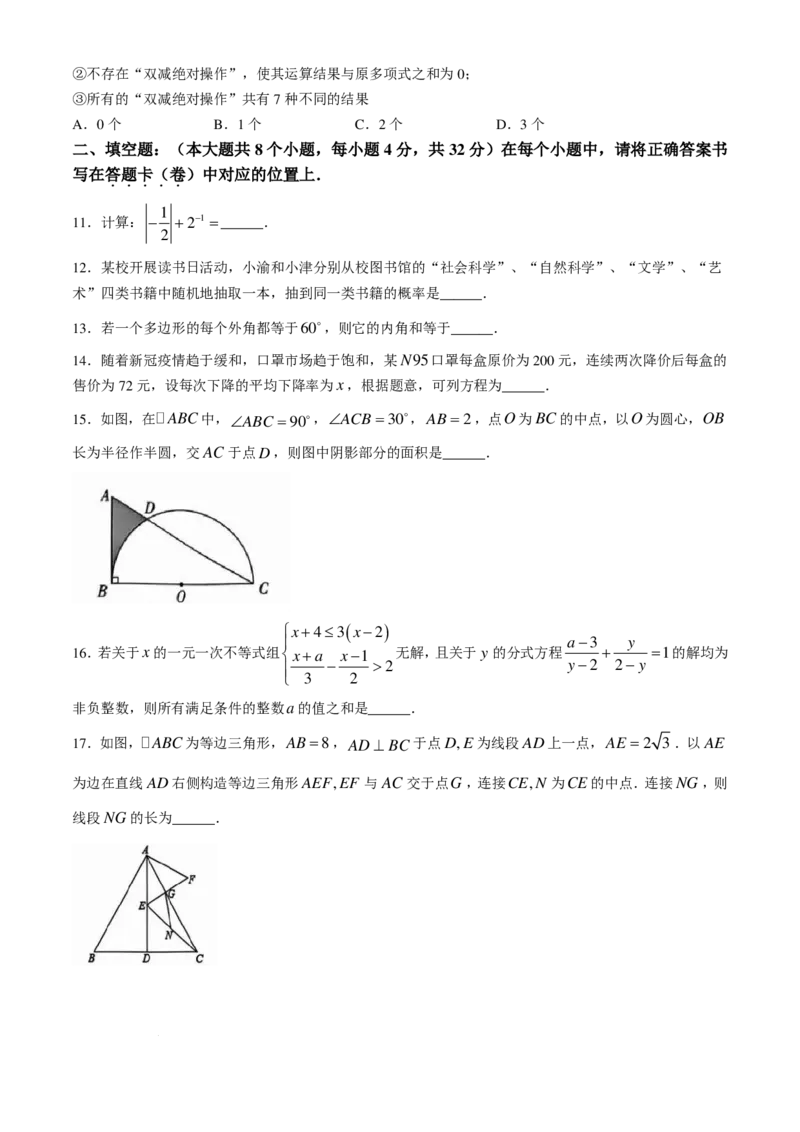15．如图，在ABC中，∠ABC =90，∠ACB=30，AB =2，点O为BC的中点，以O为圆心，OB 长为半径作半圆，交AC于点D，则图中阴影部分的面积是______． x+4≤3 ( x−2 )  a−3 y 16．若关于x的一元一次不等式组x+a x−1 无解，且关于y的分式方程 + =1的解均为  − >2 y−2 2− y  3 2 非负整数，则所有满足条件的整数a的值之和是______． 17．如图，ABC为等边三角形，AB=8，AD⊥ BC于点D,E为线段AD上一点，AE =2 3．以AE 为边在直线AD右侧构造等边三角形AEF,EF 与AC交于点G，连接CE,N 为CE的中点．连接NG，则 线段NG的长为______． 学科网（北京）股份有限公司18．一个三位自然数，若其各个数位上的数字均不为0，且百位数字等于十位数字减个位数字的差的绝对值， 则称该三位数为_____“绝对数”例如：三位数538，5= 3−8,∴538是“绝对数”则最小的“绝对数” 是______；把一个绝对数M 的任意一个数位上的数字去掉，得到三个两位数，把这三个两位数的和记为 P ( M )，把M 的百位数字的5倍，个位数字的2倍和十位数字的和记为Q ( M )．例如：对绝对数145， P ( 145 )=14+15+45=74，Q ( 145 )=1×5+5×2+4=19．已知三位数N 是一个“绝对数”，且 P ( N )−Q ( N )是一个完全平方数，则这个“绝对数”的最大值是______． 三、解答题：（本大题 8个小题，第 19题8分，其余每题各 10分，共 78分）解答时每小题 必须给出必要的演算过程或推理步骤，画出必要的图形（包括辅助线），请将解答过程书写 在答题卡中对应的位置上， 19．计算：  a  a2 −2a+1 （1）( a−1 )( 2a+3 )−2a ( a−4 ) （2） −1 ÷ a+1  a2 −1 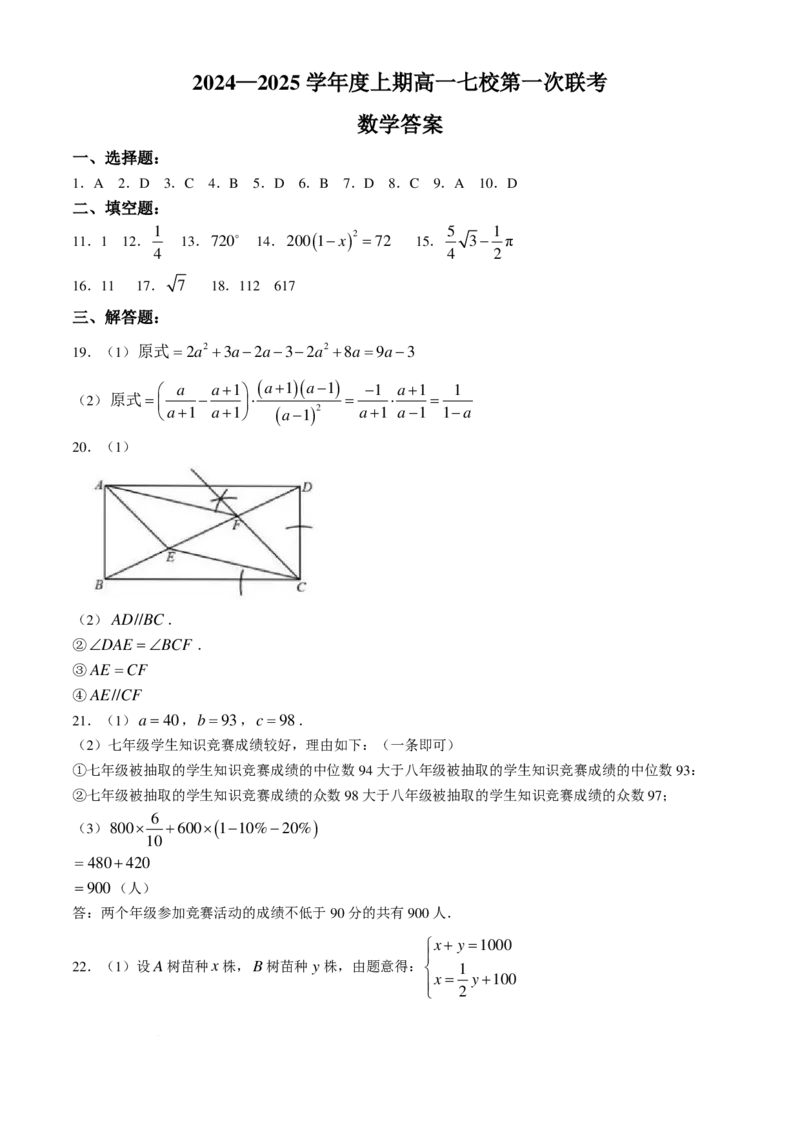20．如图，BD是矩形ABCD的对角线，∠BAD的平分线AE交BD于点E． （1）用尺规完成以下基本作图：作∠BCD的平分线交BD于点F ；连接AF,CE．（不写作法和证明， 保留作图痕迹） （2）在（1）所作的图形中，求证：四边形AECF 是平行四边形．（请补全下面的证明过程，除题目给的 字母外，不添加其它字母或者符号） 证明：四边形ABCD是矩形， ∴AD= BC,①_____． ∴∠ADE =∠CBF. 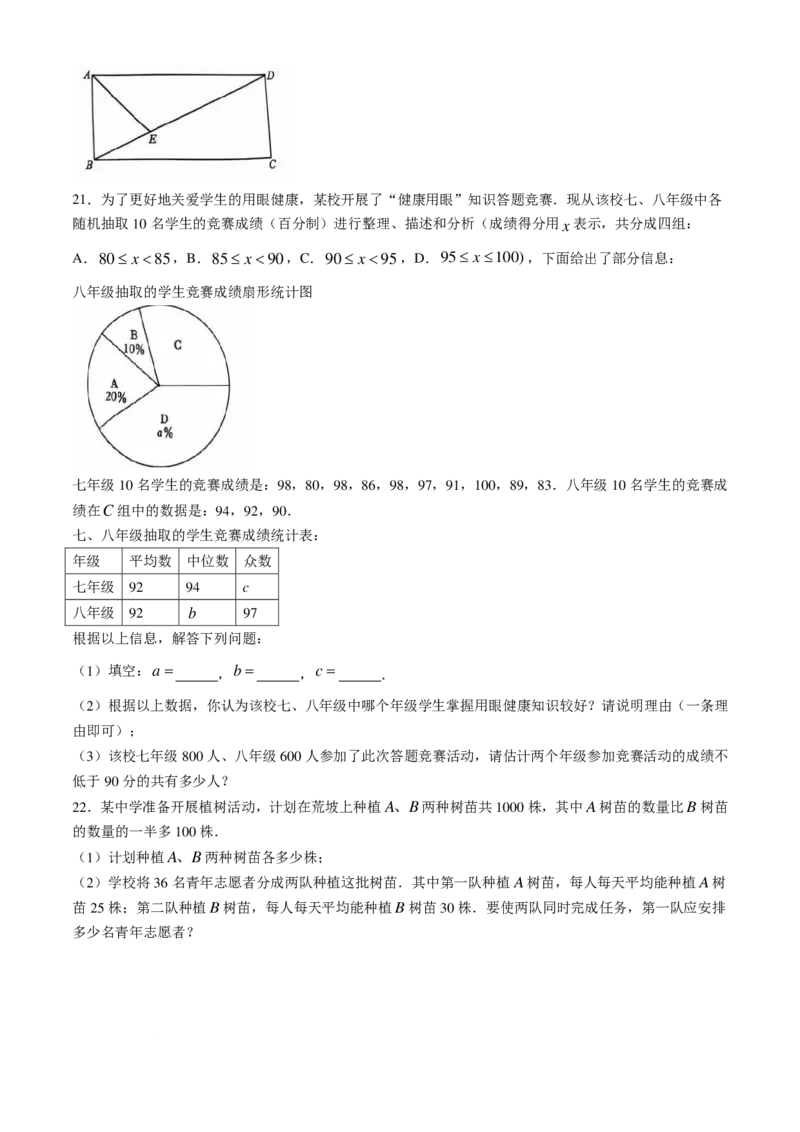AE平分∠BAD,CF 平分∠BCD 1 1 ∴∠DAE = ∠BAD ∠BCF = ∠BCD 2 ， 2 四边形ABCD是矩形，∴∠BAD=∠BCD． ∴②_____． ∴ADE ≅CBF ( ASA ) ∴∠AED=∠CFB， ③_____． ∴④_____． ∴四边形AECF 是平行四边形， 学科网（北京）股份有限公司21．为了更好地关爱学生的用眼健康，某校开展了“健康用眼”知识答题竞赛．现从该校七、八年级中各 随机抽取10名学生的竞赛成绩（百分制）进行整理、描述和分析（成绩得分用x表示，共分成四组： A．80≤ x<85，B．85≤ x<90，C．90≤ x<95，D．95≤ x≤100)，下面给出了部分信息： 八年级抽取的学生竞赛成绩扇形统计图 七年级10名学生的竞赛成绩是：98，80，98，86，98，97，91，100，89，83．八年级10名学生的竞赛成 绩在C组中的数据是：94，92，90． 七、八年级抽取的学生竞赛成绩统计表： 年级 平均数 中位数 众数 七年级 92 94 c 八年级 92 b 97 根据以上信息，解答下列问题： （1）填空：a= ______，b= ______，c= ______． （2）根据以上数据，你认为该校七、八年级中哪个年级学生掌握用眼健康知识较好？请说明理由（一条理 由即可）； （3）该校七年级800人、八年级600人参加了此次答题竞赛活动，请估计两个年级参加竞赛活动的成绩不 低于90分的共有多少人？ 22．某中学准备开展植树活动，计划在荒坡上种植A、B两种树苗共1000株，其中A树苗的数量比B树苗 的数量的一半多100株． （1）计划种植A、B两种树苗各多少株； （2）学校将36名青年志愿者分成两队种植这批树苗．其中第一队种植A树苗，每人每天平均能种植A树 苗25株；第二队种植B树苗，每人每天平均能种植B树苗30株．要使两队同时完成任务，第一队应安排 多少名青年志愿者？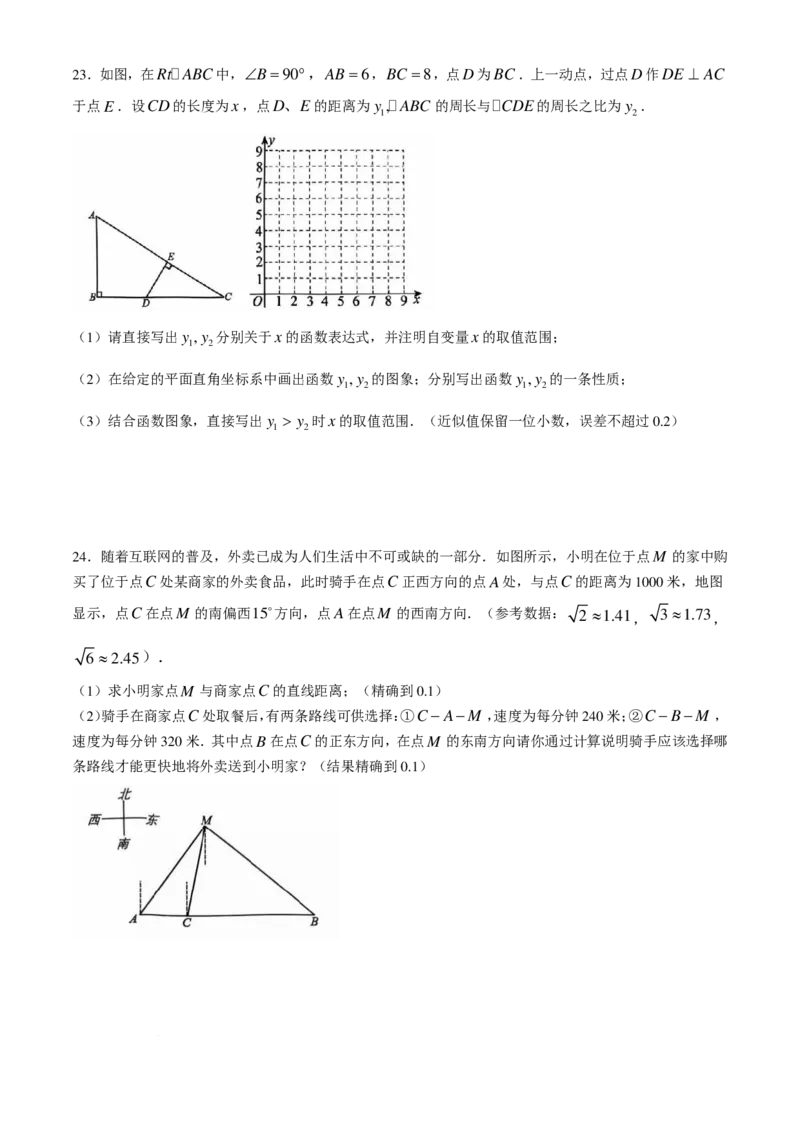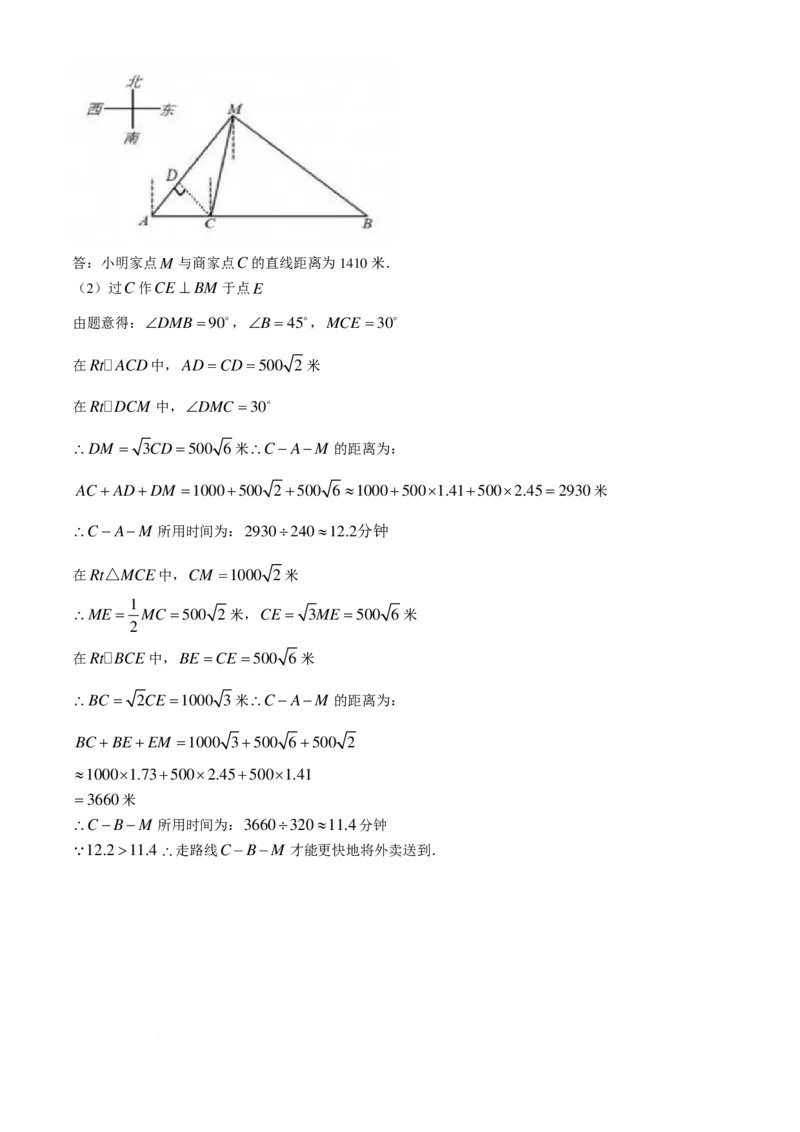 学科网（北京）股份有限公司23．如图，在RtABC中，∠B=90°，AB=6，BC =8，点D为BC．上一动点，过点D作DE ⊥ AC 于点E．设CD的长度为x，点D、E的距离为y ,ABC 的周长与CDE的周长之比为y ． 1 2 （1）请直接写出y ,y 分别关于x的函数表达式，并注明自变量x的取值范围； 1 2 （2）在给定的平面直角坐标系中画出函数y ,y 的图象；分别写出函数y ,y 的一条性质； 1 2 1 2 （3）结合函数图象，直接写出y > y 时x的取值范围．（近似值保留一位小数，误差不超过0.2） 1 2 24．随着互联网的普及，外卖已成为人们生活中不可或缺的一部分．如图所示，小明在位于点M 的家中购 买了位于点C处某商家的外卖食品，此时骑手在点C正西方向的点A处，与点C的距离为1000米，地图 显示，点C在点M 的南偏西15方向，点A在点M 的西南方向．（参考数据： 2 ≈1.41， 3 ≈1.73 ， 6 ≈2.45 ）． （1）求小明家点M 与商家点C的直线距离；（精确到0.1） （2）骑手在商家点C处取餐后，有两条路线可供选择：①C−A−M ，速度为每分钟240米；②C−B−M ， 速度为每分钟320米．其中点B在点C的正东方向，在点M 的东南方向请你通过计算说明骑手应该选择哪 条路线才能更快地将外卖送到小明家？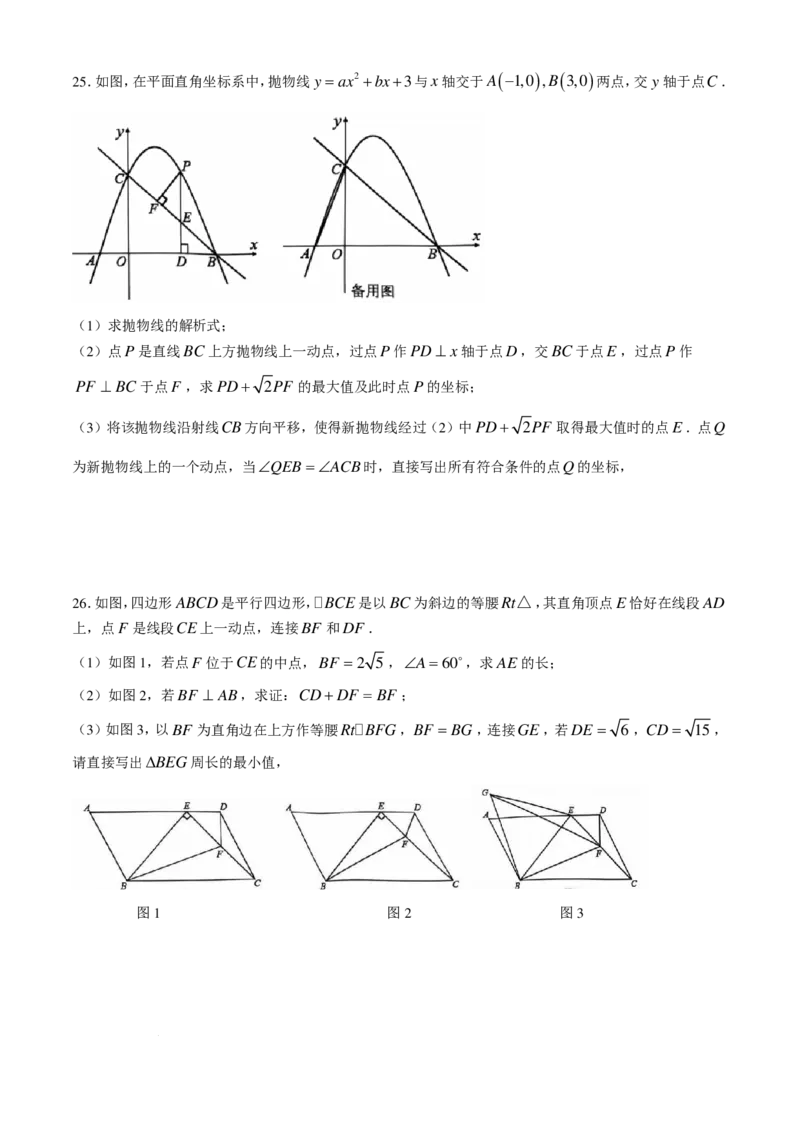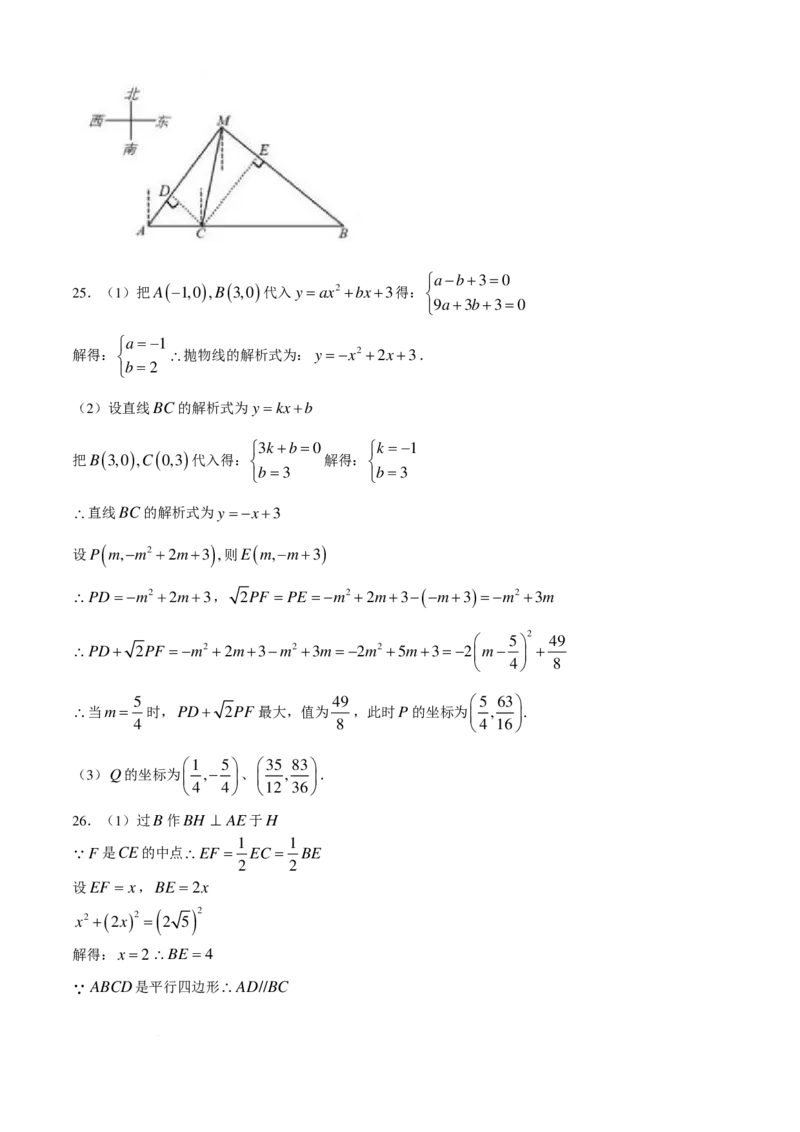（结果精确到0.1） 学科网（北京）股份有限公司25．如图，在平面直角坐标系中，抛物线y =ax2 +bx+3与x轴交于A (−1,0 ) ,B ( 3,0 )两点，交y轴于点C． （1）求抛物线的解析式； （2）点P是直线BC上方抛物线上一动点，过点P作PD⊥ x轴于点D，交BC于点E，过点P作 PF ⊥ BC于点F ，求PD+ 2PF 的最大值及此时点P的坐标； （3）将该抛物线沿射线CB方向平移，使得新抛物线经过（2）中PD+ 2PF 取得最大值时的点E．点Q 为新抛物线上的一个动点，当∠QEB=∠ACB时，直接写出所有符合条件的点Q的坐标， 26．如图，四边形ABCD是平行四边形，BCE是以BC为斜边的等腰Rt△，其直角顶点E恰好在线段AD 上，点F 是线段CE上一动点，连接BF 和DF． （1）如图1，若点F 位于CE的中点，BF =2 5，∠A=60，求AE的长； （2）如图2，若BF ⊥ AB，求证：CD+DF = BF ； （3）如图3，以BF 为直角边在上方作等腰RtBFG，BF = BG，连接GE，若DE = 6 ，CD= 15， 请直接写出∆BEG周长的最小值， 图1 图2 图3 学科网（北京）股份有限公司2024—2025 学年度上期高一七校第一次联考 数学答案 一、选择题： 1．A 2．D 3．C 4．B 5．D 6．B 7．D 8．C 9．A 10．D 二、填空题： 1 5 1 11．1 12． 13．720 14．200 ( 1−x )2 =72 15． 3− π 4 4 2 16．11 17． 7 18．112 617 三、解答题： 19．（1）原式=2a2 +3a−2a−3−2a2 +8a =9a−3  a a+1 ( a+1 )( a−1 ) −1 a+1 1 （2）原式=  −  ⋅ = ⋅ = a+1 a+1 ( a−1 )2 a+1 a−1 1−a 20．（1） （2）AD//BC． ②∠DAE =∠BCF ． ③AE =CF ④AE//CF 21．（1）a=40，b=93，c=98． （2）七年级学生知识竞赛成绩较好，理由如下：（一条即可） ①七年级被抽取的学生知识竞赛成绩的中位数94大于八年级被抽取的学生知识竞赛成绩的中位数93： ②七年级被抽取的学生知识竞赛成绩的众数98大于八年级被抽取的学生知识竞赛成绩的众数97； 6 （3）800× +600×( 1−10%−20% ) 10 =480+420 =900（人） 答：两个年级参加竞赛活动的成绩不低于90分的共有900人． x+ y =1000  22．（1）设A树苗种x株，B树苗种y株，由题意得： 1 x= y+100  2 学科网（北京）股份有限公司x=400 解得： y =600 答：计划A树苗种400株，B树苗种600株． 400 600 （2）设第一队应安排m名青年志愿者，由题意得： = 25m 33 ( 36−m ) 解得：m=16经检验：m=16是原分式方程的解，且符合题意． 答：第一队应安排16名青年志愿者． 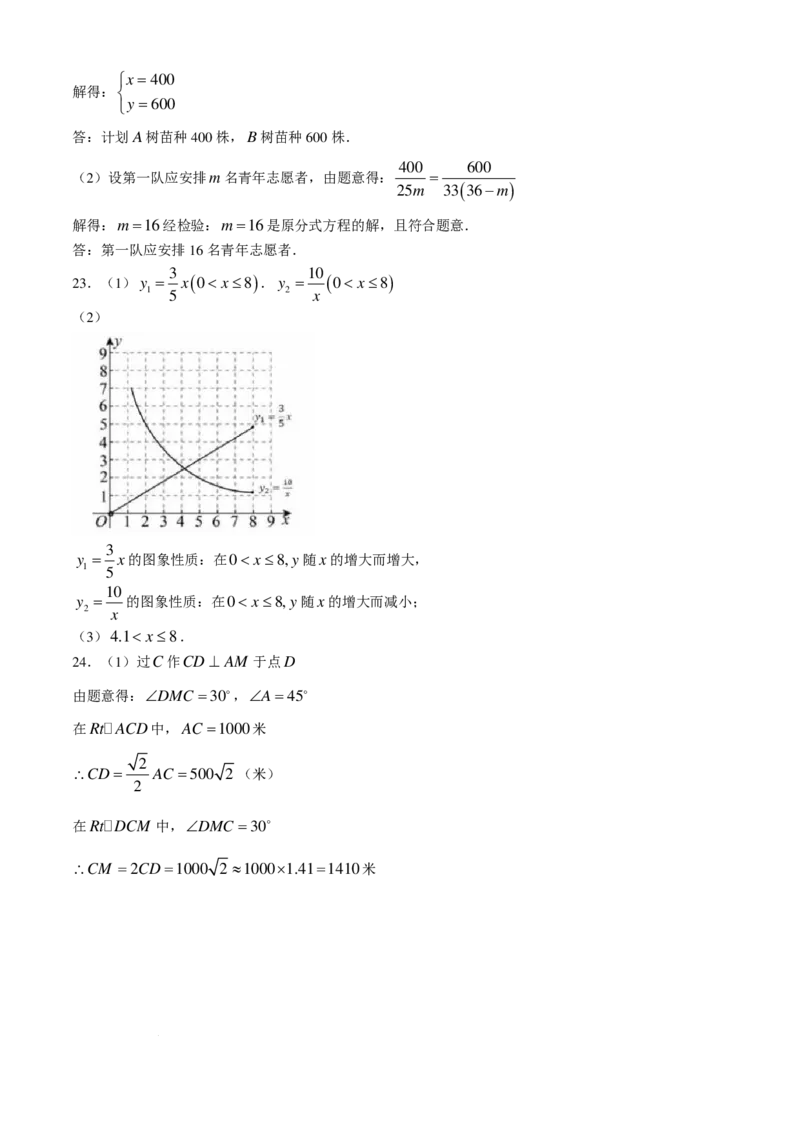3 10 23．（1）y = x ( 0< x≤8 )．y = ( 0< x≤8 ) 1 5 2 x （2） 3 y = x的图象性质：在0< x≤8,y随x的增大而增大， 1 5 10 y = 的图象性质：在0< x≤8,y随x的增大而减小； 2 x （3）4.1< x≤8． 24．（1）过C作CD⊥ AM 于点D 由题意得：∠DMC =30，∠A=45 在RtACD中，AC =1000米 2 ∴CD= AC =500 2 （米） 2 在RtDCM 中，∠DMC =30 ∴CM =2CD=1000 2 ≈1000×1.41=1410米 学科网（北京）股份有限公司答：小明家点M 与商家点C的直线距离为1410米． （2）过C作CE ⊥ BM 于点E 由题意得：∠DMB=90，∠B=45，MCE =30 在RtACD中，AD=CD=500 2 米 在RtDCM 中，∠DMC =30 ∴DM = 3CD=500 6米∴C−A−M 的距离为： AC+ AD+DM =1000+500 2+500 6 ≈1000+500×1.41+500×2.45=2930米 ∴C−A−M 所用时间为：2930÷240≈12.2分钟 在Rt△MCE中，CM =1000 2米 1 ∴ME = MC =500 2米，CE = 3ME =500 6米 2 在RtBCE中，BE =CE =500 6米 ∴BC = 2CE =1000 3米∴C−A−M 的距离为： BC+BE+EM =1000 3+500 6+500 2 ≈1000×1.73+500×2.45+500×1.41 =3660米 ∴C−B−M 所用时间为：3660÷320≈11.4分钟 12.2>11.4∴走路线C−B−M 才能更快地将外卖送到． 学科网（北京）股份有限公司a−b+3=0 25．（1）把A (−1,0 ) ,B ( 3,0 )代入y =ax2 +bx+3得： 9a+3b+3=0 a=−1 解得： ∴抛物线的解析式为：y =−x2 +2x+3． b=2 （2）设直线BC的解析式为y =kx+b 3k+b=0 k =−1 把B ( 3,0 ) ,C ( 0,3 )代入得： 解得： b=3 b=3 ∴直线BC的解析式为y =−x+3 设P ( m,−m2 +2m+3 ) ,则E ( m,−m+3 ) ∴PD=−m2 +2m+3， 2PF = PE =−m2 +2m+3−(−m+3 )=−m2 +3m 2  5 49 ∴PD+ 2PF =−m2 +2m+3−m2 +3m=−2m2 +5m+3=−2m−  +  4 8 5 49 5 63 ∴当m= 时，PD+ 2PF 最大，值为 ，此时P的坐标为  , . 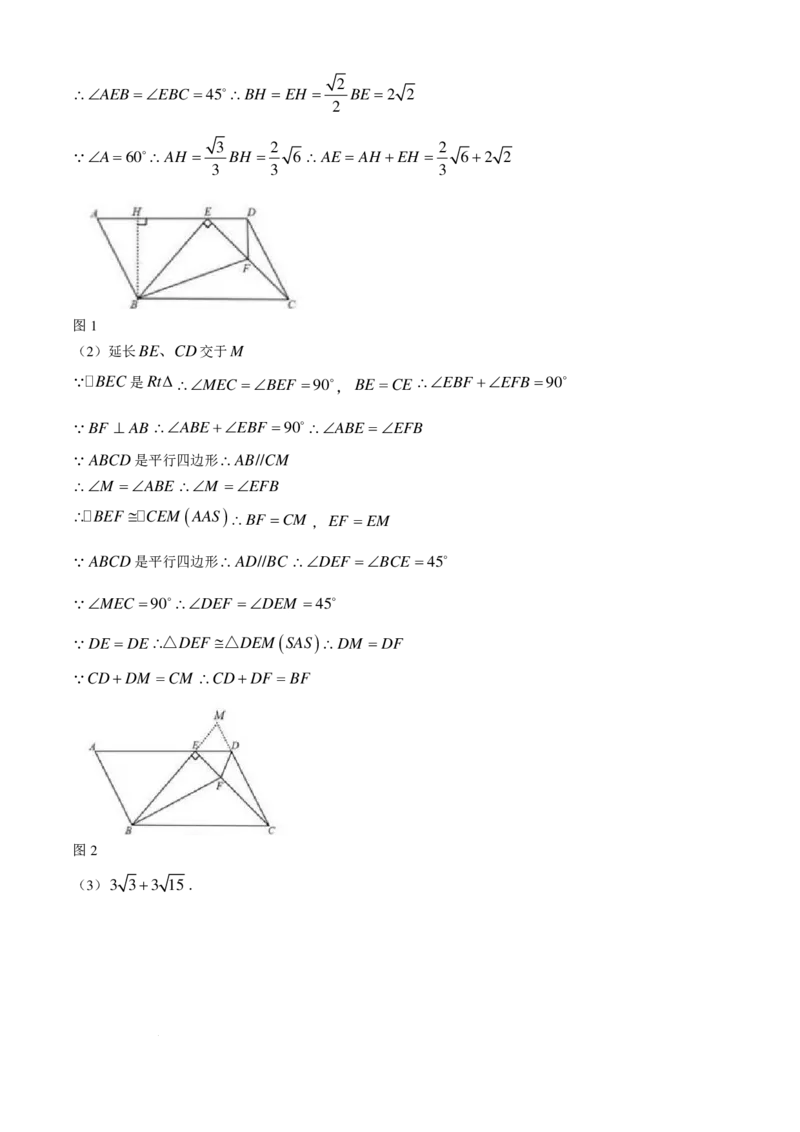4 8 4 16 1 5 35 83 （3）Q的坐标为  ,−  、  ,  ． 4 4 12 36 26．（1）过B作BH ⊥ AE于H 1 1 F是CE的中点∴EF = EC = BE 2 2 设EF = x，BE =2x x2 +( 2x )2 = ( 2 5 )2 解得：x=2∴BE =4 ∵ABCD是平行四边形∴AD//BC 学科网（北京）股份有限公司2 ∴∠AEB=∠EBC =45∴BH = EH = BE =2 2 2 3 2 2 ∠A=60∴AH = BH = 6∴AE = AH +EH = 6+2 2 3 3 3 图1 （2）延长BE、CD交于M BEC是Rt∆∴∠MEC =∠BEF =90 ，BE =CE∴∠EBF +∠EFB=90 BF ⊥ AB∴∠ABE+∠EBF =90∴∠ABE =∠EFB ABCD是平行四边形∴AB//CM ∴∠M =∠ABE∴∠M =∠EFB ∴BEF ≅CEM ( AAS ) ∴BF =CM ，EF = EM ABCD是平行四边形∴AD//BC∴∠DEF =∠BCE =45 ∠MEC =90∴∠DEF =∠DEM =45 DE = DE∴△DEF ≅△DEM ( SAS )∴DM = DF CD+DM =CM ∴CD+DF = BF 图2 （3）3 3+3 15． 学科网（北京）股份有限公司