文档内容
- 1 -
月考1 数学参考答案
1-4 ABDC 5-8 DCDB 9.AC 10.BC 11.BCD
12.19
13.
1
3
k
k
14.
9
11
,5
5,
4
2
2
第2 题详解 若
1
a 时,集合
1
M
,若
1
a 时,集合
1,
,
M
a
对于选项A,C 表示含有两个元素的集合,因此A,C 不符合;
对于选项B,当
1
a 时,
1
1
a
,当
1
a 时,集合
1
1,
a
a
,因此B 符合;
对于选项D,例如
2
a
,则
1
2
0
2
x
x
x
,此时与集合M 不相同
第8 题详解 1
1
4
4
4
4
2
2
4
4
a
b
a
b
a
b
a
b
a
b
ab
a
b
a
b
a
b
,当且仅当
2
a
b
时,取
“”成立,故选:B.
14.已知集合
Z |
2
1
M
x
a
x
a
,若集合M 有15 个真子集,则实数a 的取值范围为 .
若集合M 有15 个真子集,则M 中有4 个元素,又
Z |
2
1
M
x
a
x
a
,可知
2
1
a
a
,即
1
a ,
且区间
,2
1
a
a
中有4 个整数,当1
4
a
时,
,2
1
a
a
的区间长度为2
1
1
3
a
a
a
,此时
,2
1
a
a
中不可能有4 个整数;当
4
a
时,
,2
1
[4,7]
a
a
,其中含有4 5 6 7
、、、共4 个整数,符合题意;
当
4
a
时,
,2
1
a
a
的区间长度大于3,若
,2
1
a
a
的区间长度
1
(3,4)
a
,即4
5
a
,
若2
1
a 是整数,则区间
,2
1
a
a
中含有4 个整数,根据2
1
(7,9)
a
可知2
1
8
a
,则
9
2
a
,
此时
9
,2
1
,8
2
a
a
,其中含有5 6 7 8
、、、四个整数,符合题意;若2
1
a 不是整数,则区间
,2
1
a
a
中含
有5 6 7 8
、、、四个整数,则必须有4
5
a
且8
2
1
9
a
,解得9
5
2
a
;若
5
a
时,
,2
1
5,9
a
a
,其
中含有5 6 7 8 9
、、、、五个整数,不符合题意;若
5
a
时,
,2
1
a
a
的区间长度
1
4
a
,此时
,2
1
a
a
中有
6 7 8 9
、、、这四个整数,故2
1 10
a
,即
11
2
a
,结合
5
a
,得
11
5
2
a
;综上所述,
4
a
或9
5
2
a
或
11
5
2
a
,即实数a 的取值范围是
9
11
,5
5,
4
2
2
.故答案为:
9
11
,5
5,
4
2
2
15 .(1 )当
5
m
时,
2
2
3
5
f x
x
x
, 则不等式
0
f x
即不等式
2
2
3
5
0
x
x
, 所以
2
5
1
0,
x
x
解得
1
x 或
5
2
x
.故不等式
0
f x
的解集为{
1
x x
∣
或
5}
2
x
.
(2)因为
1
2
,
x x 是方程
0
f x
的两实根,由韦达定理知
1
2
1
2
3
2
2
x
x
m
x x
所以
2
2
2
1
2
1
2
1
2
9
2
4
x
x
x
x
x x
m
.
因为
2
2
1
2
2
x
x
,所以9
2
4
m
,解得
1
4
m
.又
2
Δ
( 3)
8
0
m
,所以
9
8
m
,故
1
4
m
.
16.解:当
0
m
时,不等式化为2
2
0
x
,解得
1
x ;
当
0
m
时,不等式化为
2
1
0
mx
x
,解得
1
x 或
2
x
m
;
当2
0
m
时, 2
1
m ,不等式化为
2
1
0
x
x
m
,解得2
1
x
m
;
当
2
m 时,不等式化为
2
1
0
x
,此时无实数解;
- 2 -
当
2
m 时, 2
1
m ,不等式化为
2
1
0
x
x
m
,解得
2
1
x
m
.
综上,
0
m
时,不等式的解集是{
1}
x x
∣
;
0
m
时,不等式的解集是
1
x x 或
2
x
m
;
2
0
m
时,不等式的解集是
2
1
x
x
m
;
2
m 时,不等式无实数解;
2
m 时,不等式的解集是
2
1
x
x
m
.
17.(1)由题知:当
1
m 时,
2
2
3
0
1
3
B
x x
x
x
x
∣
∣
,又
1
2
2
A
x
x
∣
,
1
3
A
B
x
x
∣
,
{
1
A
B
A
B
x x
R
R
R
∣
或
3}
x
;
(2)若“ x
A
”是“ x
B
”的必要不充分条件,则B 是A 的真子集,
2
2
2
3
0
3
0
B
x x
mx
m
x x
m
x
m
∣
∣
,
0
m
时,集合
3
B
x
m
x
m
∣
,
1
1
2
2
2
3
2
3
m
m
m
m
,则
1
2
m
,又
1
2
m
时,
1
3
2
2
B
x
x
∣
,符合B 是A 的真子集,可得
1
0
2
m
,综上,实数m 的取值范围为
1
0<
2
m
m
∣
.
18.(1)解:由题意知,当15
36
x
时,
2
1
8
90
1
90
10
8
10
x
x
y
x
x
x
1
90
8
2
2
10 x
x
,当且仅当1
90
10 x
x
,即
30
x
时取等号;
当36
40
x
时,
0.4
54
54
54
0.4
0.4
1.9
36
x
y
x
x
,
又
2
1.9
,∴当月研发经费为30 万元时,研发利润率取得最大值200%.
(2)由(1)可知,此时月研发经费15
36
x
,
于是,令
1
90
8
10
1.9
y
x
x
,整理得
2
61
900
0
x
x
,解得:25
36
x
.
因此,当研发利润率不小于190%时,月研发经费的取值范围是
| 25
36
x
x
.
19.
(1)由题可设
2
1
2
f
x
a x
,又
0
2
3
f
a
,得
1
a ,所以
2
2
1
2
2
3
f x
x
x
x
;
(2)由题有
2
2
3
2
1
x
x
x
m
,即
2
2
2
x
x
m
对任意的
2,2
x
恒成立,
设
2
2
h x
x
x
,则只要
max
2m
h x
即可.
2
2
1
7
2
,
[ 2,2]
2
4
h x
x
x
x
x
所以
m
2
8
ax
h x
h
,
2
8
m
,解得
4
m
;
(3)
f x 图象的对称轴为直线
1
x ,开口向上
当
1
t 时,
2
min
( )
2
3
g t
f x
f t
t
t
;当
1 1
t
t
,即1
2
t
时,
min
1
2
g t
f x
f
;
当
1 1
t 时,即当
2
t
时,
2
min
1
4
6
g t
f
x
f t
t
t
.
综上,
2
2
2
3,
1
2,1
2
4
6,
2
t
t
t
g t
t
t
t
t
.
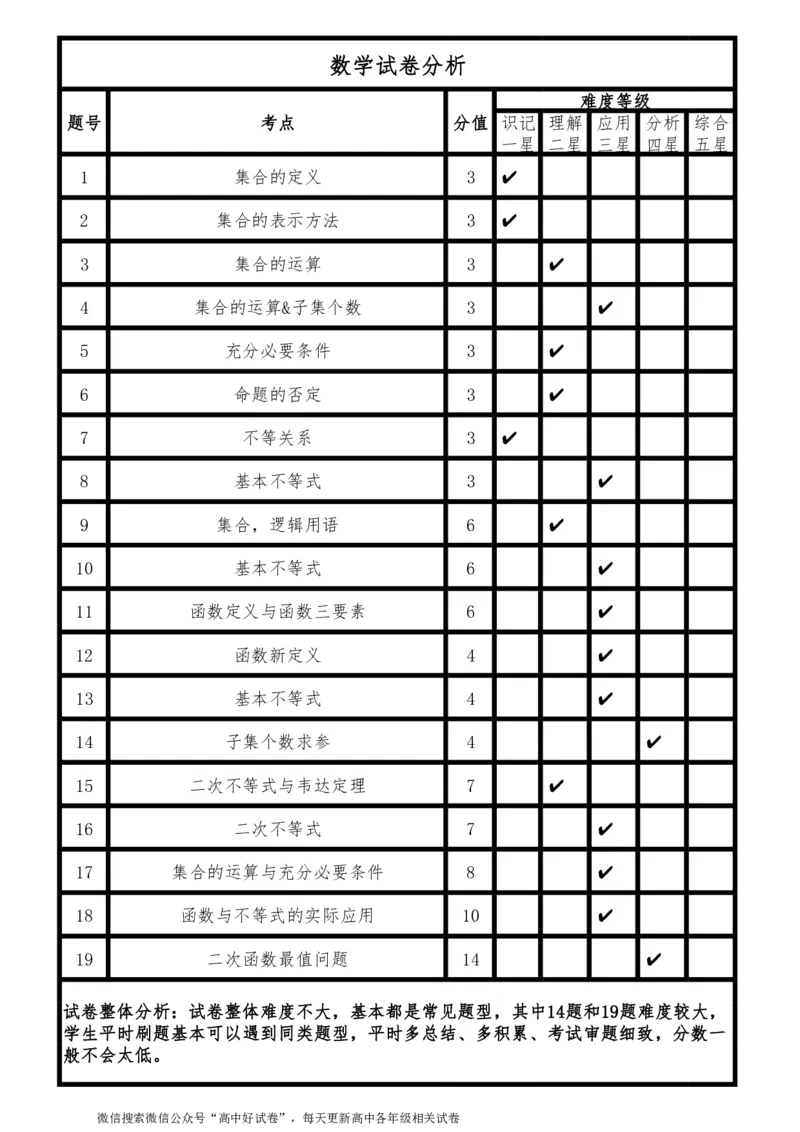
数学试卷分析
题号
考点
分值
难度等级
识记
一星
理解
二星
应用
三星
分析
四星
综合
五星
1
集合的定义
3
✔️
2
集合的表示方法
3
✔️
3
集合的运算
3
✔️
4
集合的运算&子集个数
3
✔️
5
充分必要条件
3
✔️
6
命题的否定
3
✔️
7
不等关系
3
✔️
8
基本不等式
3
✔️
9
集合,逻辑用语
6
✔️
10
基本不等式
6
✔️
11
函数定义与函数三要素
6
✔️
12
函数新定义
4
✔️
13
基本不等式
4
✔️
14
子集个数求参
4
✔️
15
二次不等式与韦达定理
7
✔️
16
二次不等式
7
✔️
17
集合的运算与充分必要条件
8
✔️
18
函数与不等式的实际应用
10
✔️
19
二次函数最值问题
14
✔️
试卷整体分析:试卷整体难度不大,基本都是常见题型,其中14题和19题难度较大,
学生平时刷题基本可以遇到同类题型,平时多总结、多积累、考试审题细致,分数一
般不会太低。
微信搜索微信公众号“高中好试卷”,每天更新高中各年级相关试卷