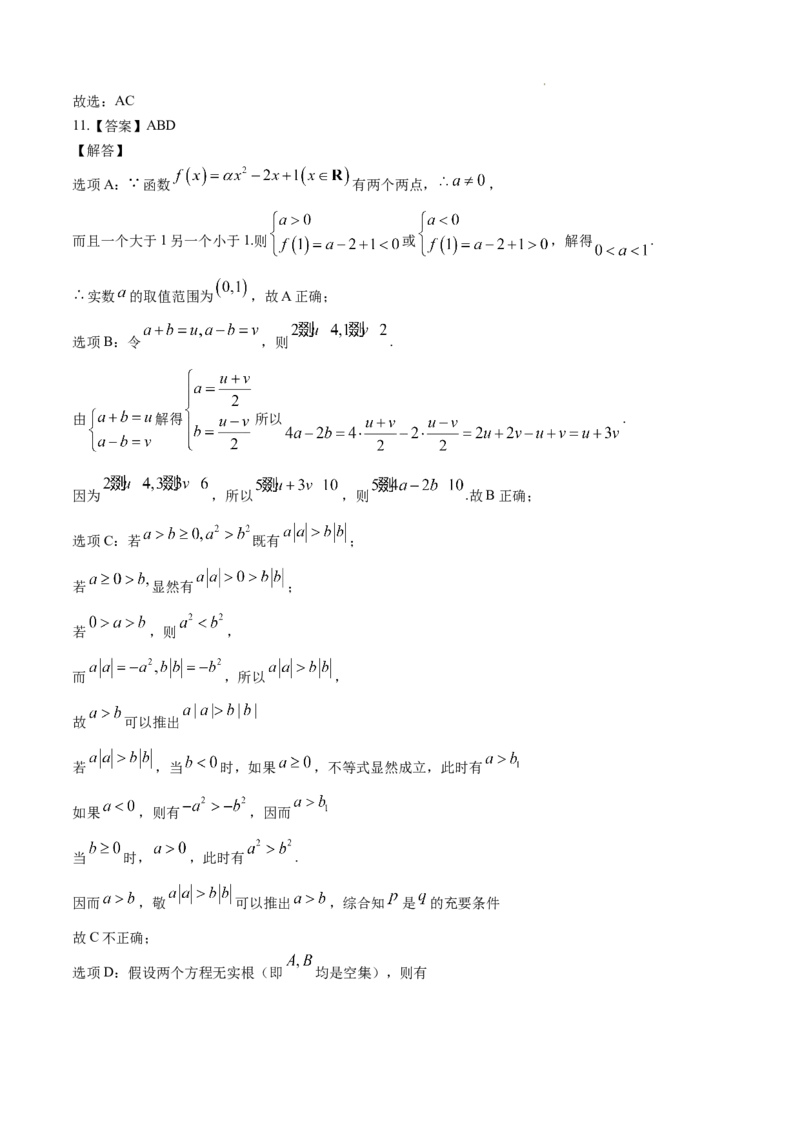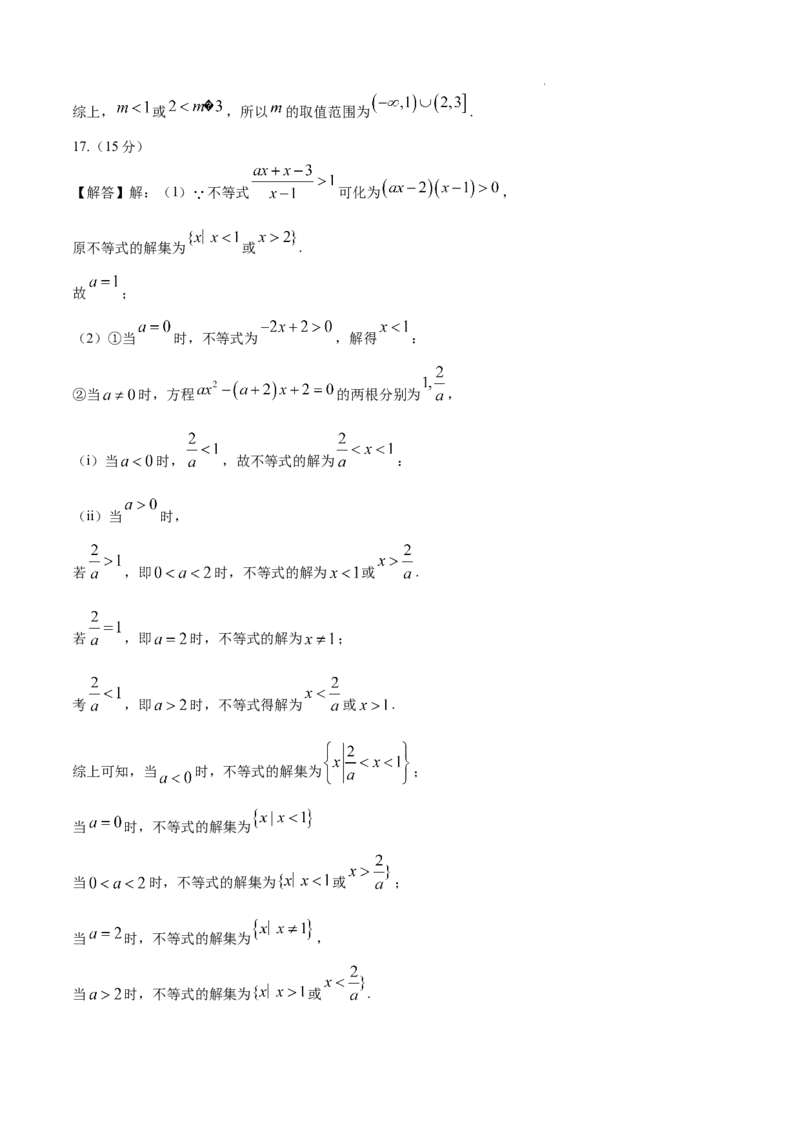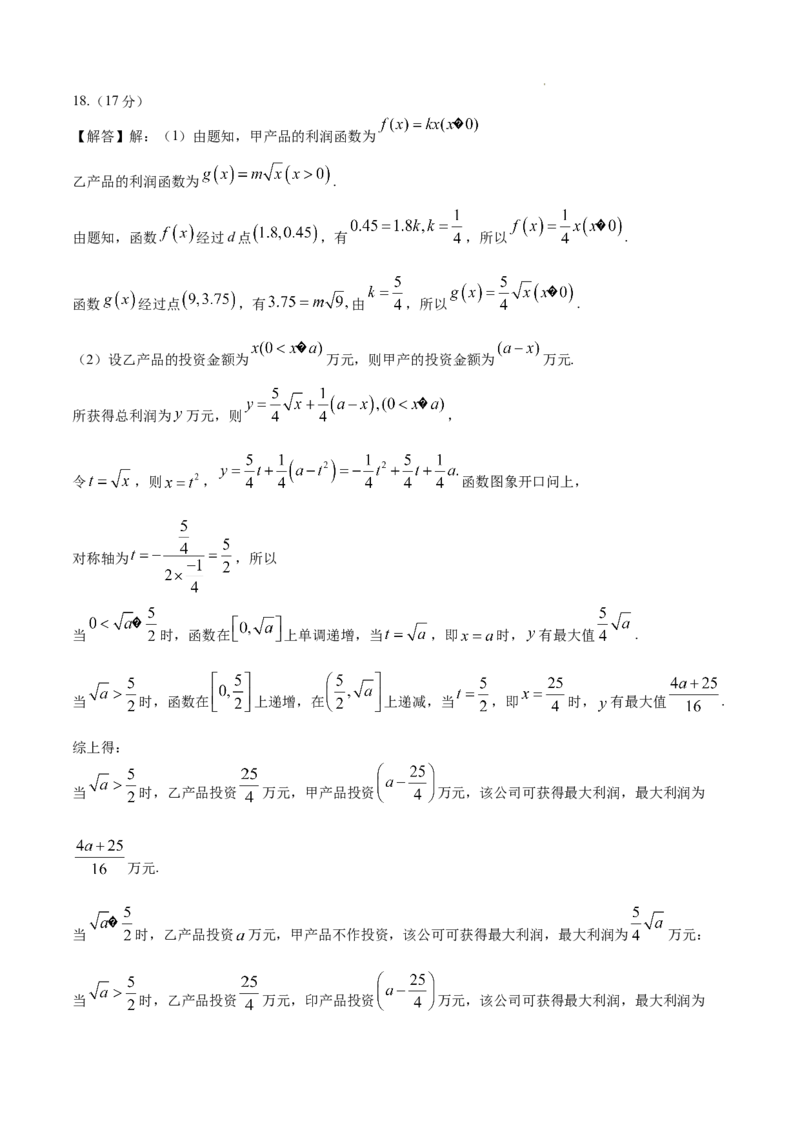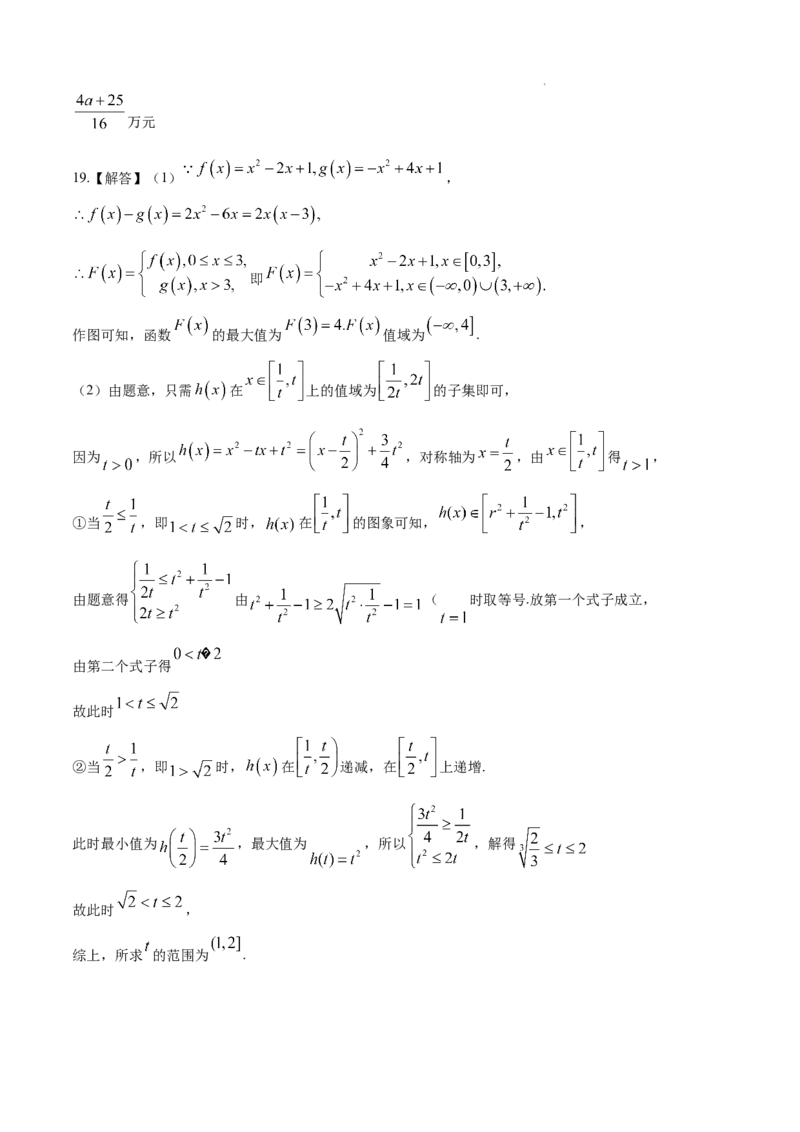文档内容
2024 年秋季鄂东南省级示范高中教育教学改革联盟学校起点考试
高一数学试题
命题学校:黄冈中学 命题教师:李钢锋
审题学校:蕲春一中 审题教师:周强锋
考试时间:2024年10月14日上午8:00—10:00 试卷满分:150分
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是
符合题目要求的.
1.已知集合 ,则 ( )
A. B. C. D.
2.命题“ ”的否定为( )
A. B.
C. D.
3.已知集合 ,则集合A的所有非空子集的个数为( )
A.5个 B.6个 C.7个 D.8个
4.下列各组函数表示相同函数的是( )
A. B.
C. D.
5.设 ,则“ ”是“ ”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
6.已知 ,则正确的结论是( )
A. B.
C. D. 与 的大小不确定
7.已知关于 的不等式 的解集为 ,则关于 的不等式 的解集
学科网(北京)股份有限公司为( )
A. B. ,或
C. D.
8.若正实数 满足 ,不等式 有解,则 的取值范围是( )
A. B.
C. D.
二、多选题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目
要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.
9.图中阴影部分用集合符号可以表示为( )
A. B.
C. D.
10.若 ,且 ,则下列说法正确的是( )
A. 有最大值 B. 有最大值2
C. 有最小值5 D. 有最小值
11.下列命题正确的有( )
A.若方程 有两个根,一个大于1另一个小于1,则实数 的取值范围为
B.设 ,若 且 ,则
学科网(北京)股份有限公司C.设 ,命题 是命题 的充分不必要条件
D.若集合 和 至少有一个集合不是空集,则实数
的取值范围是 或
三、填空题:本题共3小题,每小题5分,共15分.
12.已知函数 的定义域为 ,则函数 的定义域为______.
13.已知 为二次函数,满足 ,则函数 ______.
14.设集合 ,函数 ,已知 ,且 ,则 的取
值范围为______.
四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.
15.(13分)已知集合 .
(1)若 ,求 ;
(2)若 ,求实数 的取值范围.
16.(15分)设命题 :对任意 ,不等式 恒成立,命题 :存在 使得
不等式 成立.
(1)若 为真命题,求实数 的取值范围;
(2)若命题 与命题 一真一假,求实数 的取值范围.
17.(15分)已知关于 的不等式 .
(1)若不等式的解集为 或 ,求 的值;
(2)求关于 的不等式的解集.
18.(17分)某公司销售甲、乙两种产品,根据市场调查和预测,甲产品的利润 (万元)与投资额 (万
元)成正比,其关系如图(1)所示;乙产品的利润 (万元)与投资额 (万元)的算术平方根成正比,
其关系式如图(2)所示,
学科网(北京)股份有限公司(1)分别将甲、乙两种产品的利润表示为投资额的函数;
(2)若该公司投资 万元资金,并全部用于甲、乙两种产品的营销,问:怎样分配这 万元投资,
才能使公司获得最大利润?其最大利润为多少?
19.(17分)设 ,其中 ,记 .
(1)若 ,求 的值域;
(2)若 ,记函数 对任意 ,总存在 ,使得 成
立,求实数 的取值范围;
(3)若 ,求实数 的取值范围.
学科网(北京)股份有限公司2024 年秋季鄂东南省级示范高中教育教学改革联盟学校起点考试
高一数学参考答案
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是
符合题目要求的.
1.【答案】D
【详解】因为 ,所以 .故选:D.
2.【答案】B
【详解】由全称命题的否定为特称命题知:原命题的否定为:
故选:B
3.【答案】C
【详解】由题设, ,即8可被 整除且 ,
故集合A的所有非空子集的个数为
4.【答案】D
【解答】解: 与 的对应关系不同,不是同一函数:
学科网(北京)股份有限公司定义域不同,不是同一函数:
的定义域为 , 而的定义域为 ,不是同一函数:
与 的定义域都为 ,对应关系相同,是同一函数.
故途:D.
5.【答案】D
【解答】根据题意,不等式 ,则 ,即 ,解集为
不等式 ,即 ,解集为 ,
因为 且 ,
所以“ ”是“ ”的既不充分也不必要条件,
故选:D.
6.【解新】方法一:特值法
取特殊值,令 ,则
易知 ,排除B,C,还不能排除D,猜测选A.
方法二:作差法,分析法
要比较 大小,只需要比较 与 的大小
比较 与 的大小(遇到二次根式可考虑平方去掉恨号)
比较 与 的大小
比较 与 的大小.
而显然 .故 ,故 .故选:A.
方法三:有理化法
学科网(北京)股份有限公司,则 ,故选A.
7.【答案】A
【解答】因为不等式 的解集为 ,
所以2和3是方程 的两个实数解,且 ;
由根和系数的关系知, 所以 ;
所以不等式 可化为 ,叫 ,解得 ,
所求不等式的解集为
故选:A.
8.【答栥】B
【详解】由
,
仅当 ,即 时等号成立.
要使不等式 有解,只需 .
学科网(北京)股份有限公司所以 .
故选:B
二、多选题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目
要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.
9.【答案】AD
【解答】解:图中阴影部分用集合符号可以表示为 或 .
故选:AD.
10.【答案】AC
【解答】解:对于A, ,
当且仅当 且 ,当 时取等号,不以 有最大值 故A正确,
对于B.因为 .
所以 ,当且仅当 时取等号,
所以 有最大值 ,故B错误
对于C, ,
当且仅当 且 叫 且 ,即 时取等号,
所以 有最小值5,故C正确
对于D.因为 .所以 ,
所以 ,当且仅当 且 ,即 时取等号,
所以 有最小值 ,故 错误.
学科网(北京)股份有限公司故选:AC
11.【答案】ABD
【解答】
选项A: 函数 有两个两点, ,
而且一个大于1另一个小于1.则 或 ,解得 .
实数 的取值范围为 ,故A正确;
选项B:令 ,则 .
由 解得 所以 .
因为 ,所以 ,则 .故B正确;
选项C:若 既有 ;
若 显然有 ;
若 ,则 ,
而 ,所以 ,
故 可以推出
若 ,当 时,如果 ,不等式显然成立,此时有
如果 ,则有 ,因而
当 时, ,此时有 .
因而 ,敬 可以推出 ,综合知 是 的充要条件
故C不正确;
选项D:假设两个方程无实根(即 均是空集),则有
学科网(北京)股份有限公司解得 .
所以当 或 时,两个方程至少有一个方程有实根,即两个集合至少有一个不是空集.
故填 或 ,故D正确
三、填空题:本题共3小题,每小题5分,共15分.
12.【答案】
【详解】由题意得: ,解得: ,
由 ,解得: ,
故函数的定义域是 .
13.【答案】
【解答】解:设 ,满足 ,
所以 ,
解得
则函数 .
14.【答案】
【解答】解:因为 .所以 ,
则 ,
由 ,可得 ,
学科网(北京)股份有限公司解得 .
故答案为: .
四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.
15.(13分)【解答】解:(1) 时, ,则 或 ,
则 或
(2) ,等价于 ,
当 ,则 ,船得 ,符合题意
当 .则 ,解得 .
综上,实数 的取值范围为
16.(15分)【解析】(1)因为 为真命题,所以对任意 不等式 恒成立,
所以 其中 ,所以 ,解得 ,
有以 的取值范围 ,
(2)若 为真命题,即存在 .使得不等式 成立,
则 ,其中 ,1],而 ,
所以 ,故 :因为 一真一假.
所以 为真命题, 为假命题或 为假命题, 为真命题,
若 为真命题, 为假命题,则 ,所以 ;
若 为假命题, 为真命题.则 或 ,所以 .
学科网(北京)股份有限公司综上, 或 ,所以 的取值范围为 .
17.(15分)
【解答】解:(1) 不等式 可化为 ,
原不等式的解集为 或 .
故 ;
(2)①当 时,不等式为 ,解得 :
②当 时,方程 的两根分别为 ,
(i)当 时, ,故不等式的解为 :
(ii)当 时,
若 ,即 时,不等式的解为 或 .
若 ,即 时,不等式的解为 ;
考 ,即 时,不等式得解为 或 .
综上可知,当 时,不等式的解集为 ;
当 时,不等式的解集为
当 时,不等式的解集为 或 ;
当 时,不等式的解集为 ,
当 时,不等式的解集为 或 .
学科网(北京)股份有限公司18.(17分)
【解答】解:(1)由题知,甲产品的利润函数为
乙产品的利润函数为 .
由题知,函数 经过d点 ,有 ,所以 .
函数 经过点 ,有 由 ,所以 .
(2)设乙产品的投资金额为 万元,则甲产的投资金额为 万元.
所获得总利润为 万元,则 ,
令 ,则 , 函数图象开口问上,
对称轴为 ,所以
当 时,函数在 上单调递增,当 ,即 时, 有最大值 .
当 时,函数在 上递增,在 上递减,当 ,即 时, 有最大值 .
综上得:
当 时,乙产品投资 万元,甲产品投资 万元,该公司可获得最大利润,最大利润为
万元.
当 时,乙产品投资 万元,甲产品不作投资,该公可可获得最大利润,最大利润为 万元:
当 时,乙产品投资 万元,印产品投资 万元,该公司可获得最大利润,最大利润为
学科网(北京)股份有限公司万元
19.【解答】(1) ,
即
作图可知,函数 的最大值为 值域为 .
(2)由题意,只需 在 上的值域为 的子集即可,
因为 ,所以 ,对称轴为 ,由 得 ,
①当 ,即 时, 在 的图象可知, ,
由题意得 由 ( 时取等号.放第一个式子成立,
由第二个式子得
故此时
②当 ,即 时, 在 递减,在 上递增.
此时最小值为 ,最大值为 ,所以 ,解得
故此时 ,
综上,所求 的范围为 .
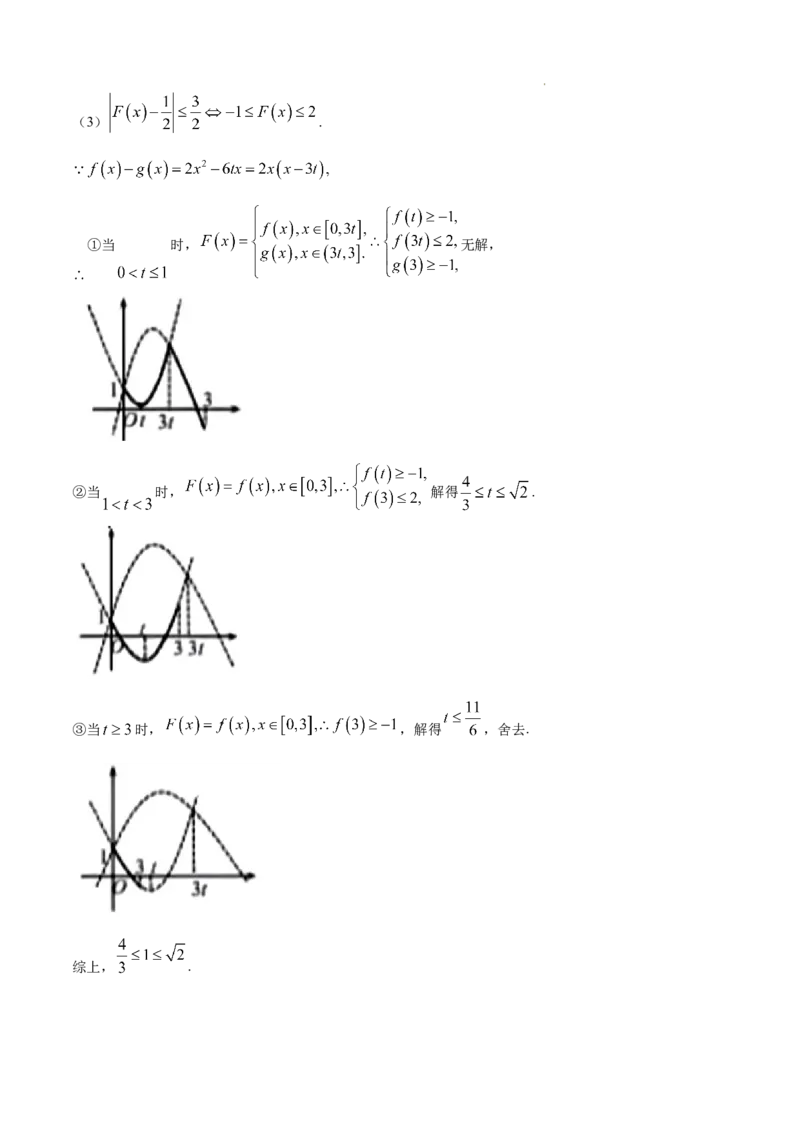
学科网(北京)股份有限公司(3) .
①当 时, 无解,
②当 时, 解得 .
③当 时, ,解得 ,舍去.
综上, .
学科网(北京)股份有限公司