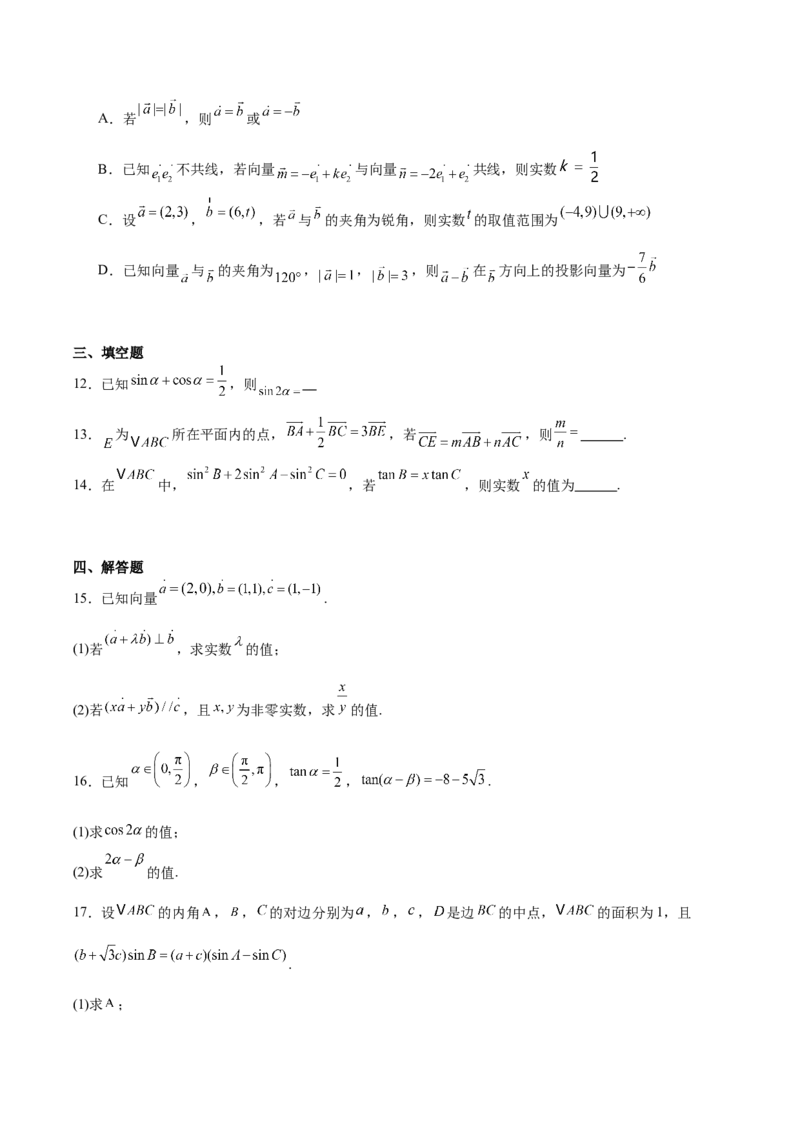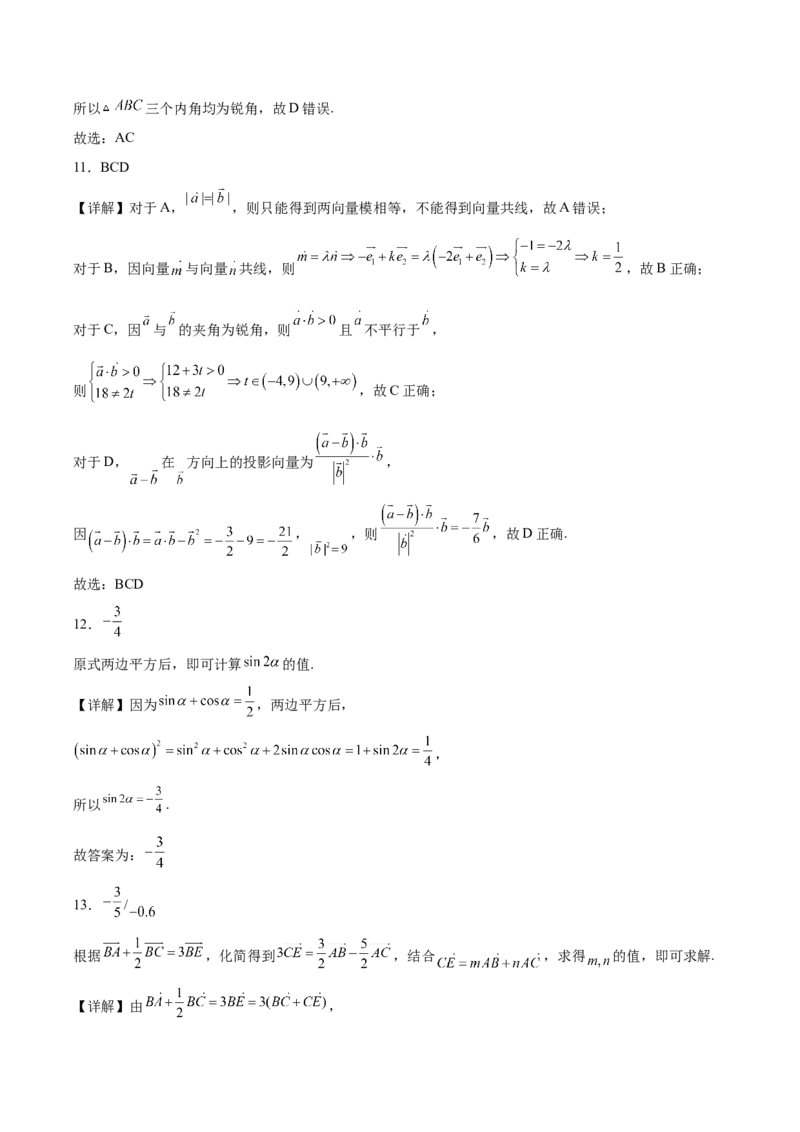文档内容
江苏省泗阳县2024-2025学年高一下学期期中考试
数学试卷
一、单选题
1.下列命题正确的是( )
A.单位向量均相等 B.任一向量与它的相反向量不相等
C.模为零的向量与任一向量平行 D.模相等的两个共线向量是相同的向量
2.在△ABC中,若 ,则
A. B. C. D. 或
3.已知 , ,若 , ,则 的值为( )
A. B. C. D.
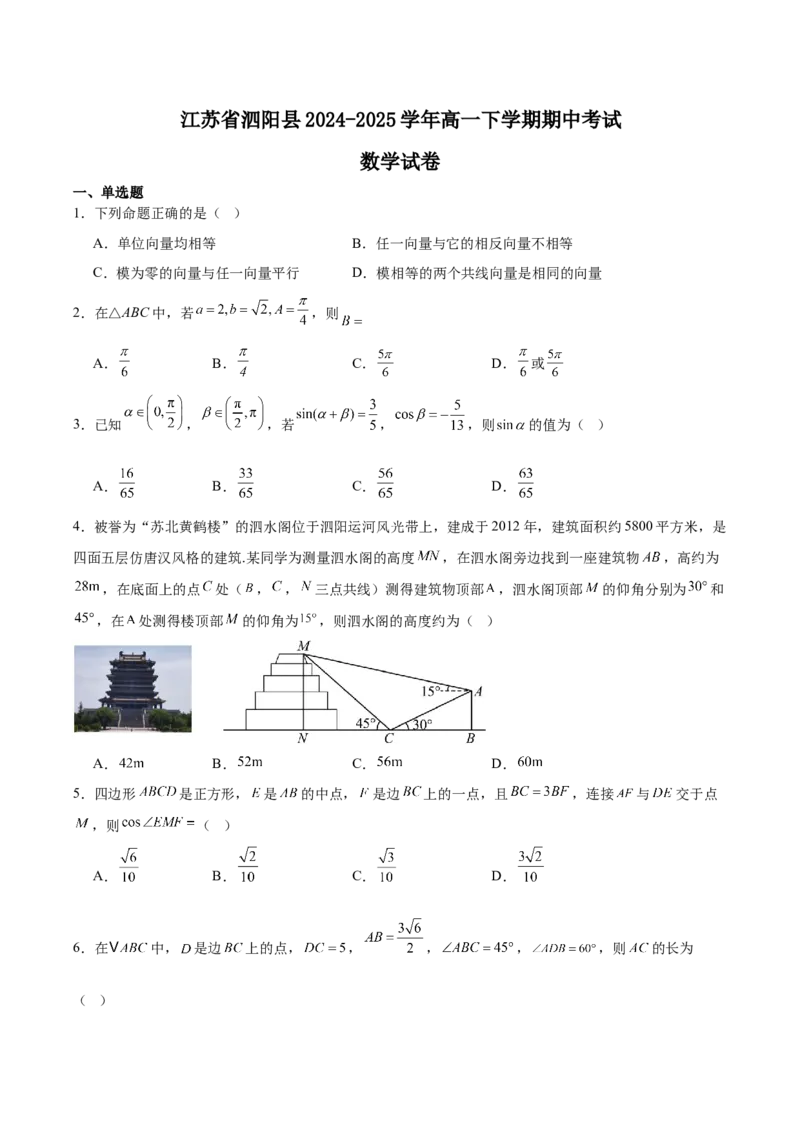
4.被誉为“苏北黄鹤楼”的泗水阁位于泗阳运河风光带上,建成于2012年,建筑面积约5800平方米,是
四面五层仿唐汉风格的建筑.某同学为测量泗水阁的高度 ,在泗水阁旁边找到一座建筑物 ,高约为
,在底面上的点 处( , , 三点共线)测得建筑物顶部 ,泗水阁顶部 的仰角分别为 和
,在 处测得楼顶部 的仰角为 ,则泗水阁的高度约为( )
A. B. C. D.
5.四边形 是正方形, 是 的中点, 是边 上的一点,且 ,连接 与 交于点
,则 ( )
A. B. C. D.
6.在 中, 是边 上的点, , , , ,则 的长为
( )A.5 B.7 C.9 D.11
7.图中正方形 的边长为2,圆 的半径为5,正方形的中心与圆的圆心重合,动点 在圆上,则
的值为( )
A.23 B.29 C.21 D.24
8.在 中,角 的对边分别为 且 ,若 ,则 的周长
的最大值为( )
A. B. C.6 D.8
二、多选题
9.以下正确的有( )
A.
B.
C.函数 的最大值为2
D.
10. 的内角 , , 的对边分别为 , , ,则下列说法正确的有( )
A.若 ,则
B. ,则 为等腰三角形
C. , , ,则 有两解
D.若 ,则 可以是钝角三角形
11.下列说法正确的有( )A.若 ,则 或
B.已知 不共线,若向量 与向量 共线,则实数
C.设 , ,若 与 的夹角为锐角,则实数 的取值范围为
D.已知向量 与 的夹角为 , , ,则 在 方向上的投影向量为
三、填空题
12.已知 ,则
13. 为 所在平面内的点, ,若 ,则 .
14.在 中, ,若 ,则实数 的值为 .
四、解答题
15.已知向量 .
(1)若 ,求实数 的值;
(2)若 ,且 为非零实数,求 的值.
16.已知 , , , .
(1)求 的值;
(2)求 的值.
17.设 的内角 , , 的对边分别为 , , , 是边 的中点, 的面积为1,且
.
(1)求 ;(2)求 的值.
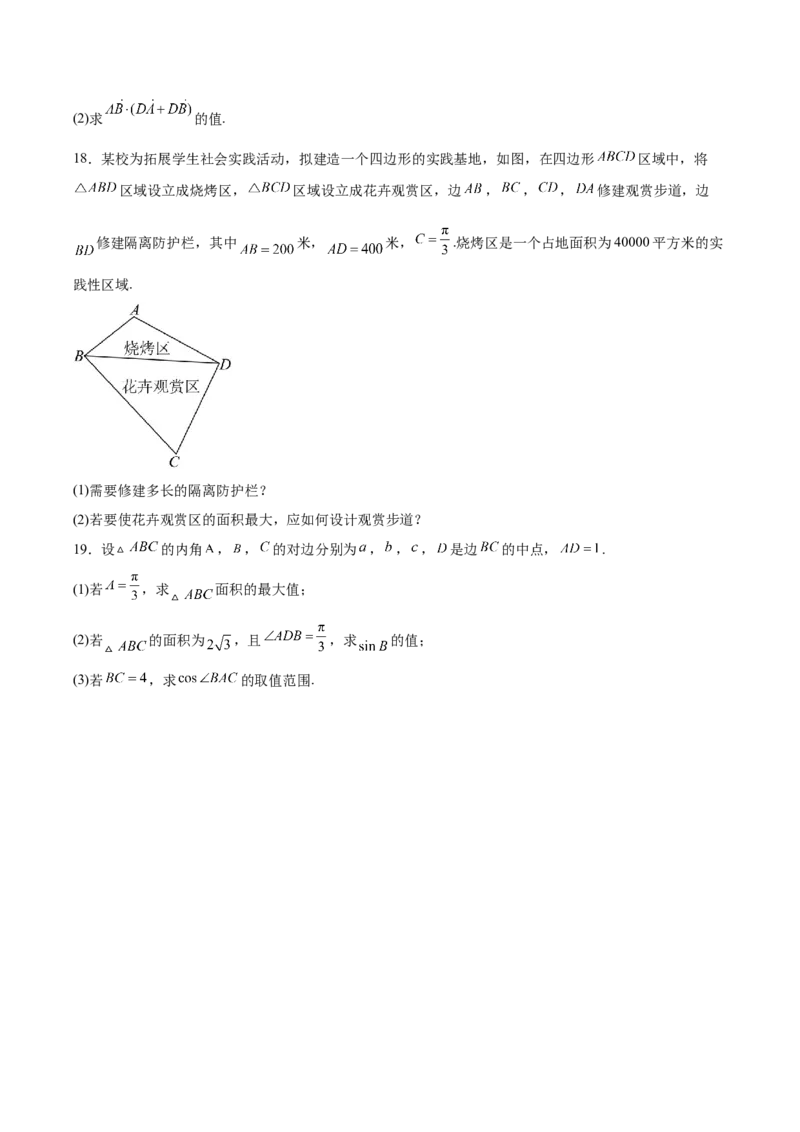
18.某校为拓展学生社会实践活动,拟建造一个四边形的实践基地,如图,在四边形 区域中,将
区域设立成烧烤区, 区域设立成花卉观赏区,边 , , , 修建观赏步道,边
修建隔离防护栏,其中 米, 米, .烧烤区是一个占地面积为40000平方米的实
践性区域.
(1)需要修建多长的隔离防护栏?
(2)若要使花卉观赏区的面积最大,应如何设计观赏步道?
19.设 的内角 , , 的对边分别为 , , , 是边 的中点, .
(1)若 ,求 面积的最大值;
(2)若 的面积为 ,且 ,求 的值;
(3)若 ,求 的取值范围.题号 1 2 3 4 5 6 7 8 9 10
答案 C A B C B B A C BCD AC
题号 11
答案 BCD
1.C
根据单位向量、零向量、共线向量的定义判断即可.
【详解】对于A:单位向量大小相等都是 ,但方向不一定相同,故单位向量不一定相等,故A错误;
对于B:零向量与它的相反向量相等,故B错误.
对于C:模为 的向量为零向量,零向量与任非零意向量共线,故C正确;
对于D:模相等的两个共线向量可能是相同的向量也可能是相反向量,故D错误.
故选:C.
2.A
【详解】由正弦定理有 ,所以 , ,又因为 ,故 ,选
A.
3.B
由 结合题意,正弦差角公式可得答案.
【详解】 .
因 , ,则 ,又 ,
则 ,又 .
则 .
故选:B
4.C
在 中求得 ,然后在 中,利用正弦定理求得 即可求解.
【详解】在 中, ,所以 ,
在 中, ,则 ,
由正弦定理得 ,即 ,解得 ,
在 中, .
故选:C.
5.B
建立平面直角坐标系,设正方形 的边长为3,写出点的坐标,利用向量夹角余弦公式进行求解.
【详解】以 为坐标原点, 所在直线分别为 轴,建立平间直角坐标系,
设正方形 的边长为3,
则 ,
故 ,
所以 .
故选:B
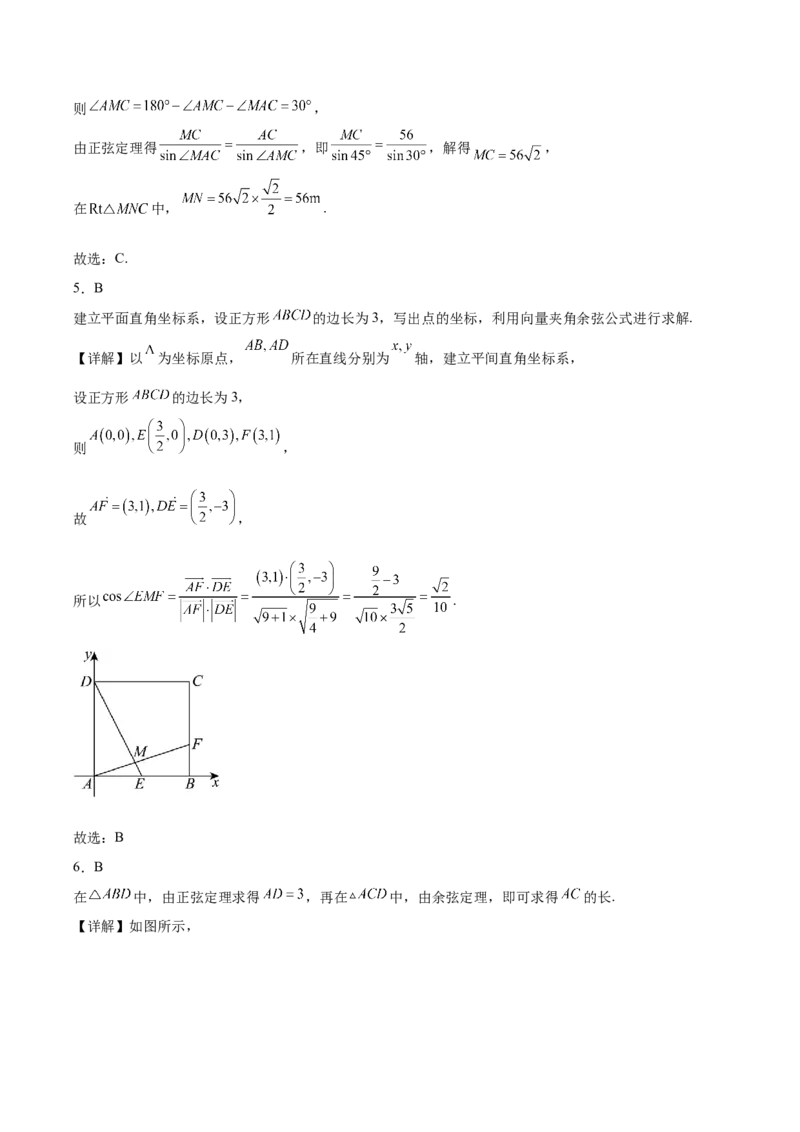
6.B
在 中,由正弦定理求得 ,再在 中,由余弦定理,即可求得 的长.
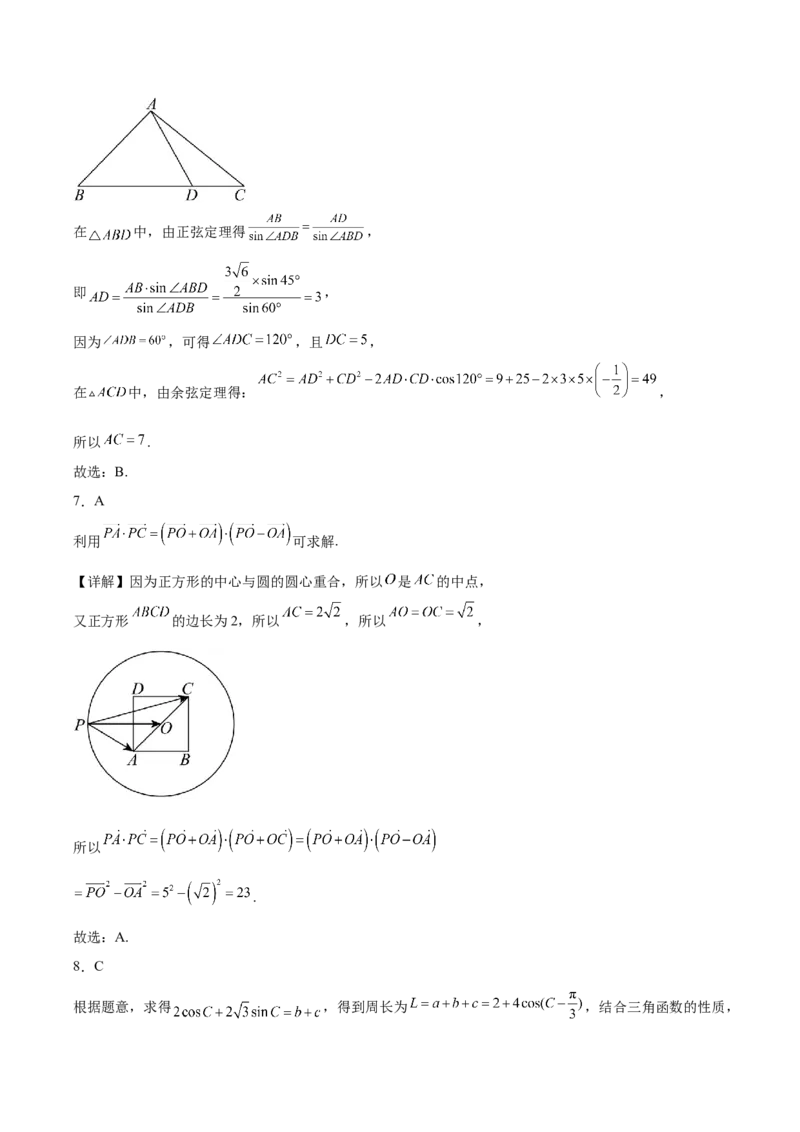
【详解】如图所示,在 中,由正弦定理得 ,
即 ,
因为 ,可得 ,且 ,
在 中,由余弦定理得: ,
所以 .
故选:B.
7.A
利用 可求解.
【详解】因为正方形的中心与圆的圆心重合,所以 是 的中点,
又正方形 的边长为2,所以 ,所以 ,
所以
.
故选:A.
8.C
根据题意,求得 ,得到周长为 ,结合三角函数的性质,即可求解.
【详解】由 且 ,可得 ,
又由 ,即 ,
所以 的周长为 ,
当 时,即 时,周长 取得最大值,最大值为 .
故选:C.
9.BCD
利用三角恒等变换公式逐项计算可得结论.
【详解】对于A,
,故A错误;
对于B,
,故B正确;
对于C,
,
当且仅当 时,等号成立,故函数 的最大值为2,故C正确;对于D,
,故D正确.
故选:BCD.
10.AC
【详解】对于A,因为 ,所以由正弦定理可得 ,又大边对大角,则 ,故A正确;
对于B,由 ,得 ,所以由余弦定理得 ,
所以 ,得 ,
所以 ,所以 ,
所以 或 ,所以 为等腰三角形或直角三角形,故B错误;
对于C,过 作 于点 ,则 ,
因为 ,所以 有两解,故C正确;
对于D,因为 , ,
所以 ,
因为 ,且 不可能有两个钝角,所以 ,所以 三个内角均为锐角,故D错误.
故选:AC
11.BCD
【详解】对于A, ,则只能得到两向量模相等,不能得到向量共线,故A错误;
对于B,因向量 与向量 共线,则 ,故B正确;
对于C,因 与 的夹角为锐角,则 且 不平行于 ,
则 ,故C正确;
对于D, 在 方向上的投影向量为 ,
因 , ,则 ,故D正确.
故选:BCD
12.
原式两边平方后,即可计算 的值.
【详解】因为 ,两边平方后,
,
所以 .
故答案为:
13. /
根据 ,化简得到 ,结合 ,求得 的值,即可求解.
【详解】由 ,可得 ,
因为 ,所以 ,可得 .
故答案: .
14.
先利用正弦定理化简得 ,再根据余弦定理得出 为钝角,最后利用正弦定理和余弦定理化
简 即可.
【详解】利用正弦定理则 可化简为 ,
则 ,
因 ,则 ,则 ,
因 ,则利用正弦定理和余弦定理有
.
故答案为: .
15.(1)
(2)
【详解】(1)解:因为 ,可得 ,
因为 ,所以 ,解得 .
(2)解:因为 ,
可得 ,又因为 ,所以 ,可得 ,
因为 为非零实数,所以 .
16.(1)
(2)
【详解】(1)因为 , ,所以
又因为 ,所以 ,
所以 .
(2)因为 , ,所以 ,所以
又因为 ,
所以 , ,
因为
所以
因为 ,所以
17.(1)
(2)
【详解】(1)因为 ,
所以由正弦定理得 ,所以 ,
所以 ,
因为 , ;
(2)因为 ,
,
,
.
18.(1) 米
(2)应使观赏步道 米
(1)由三角形面积公式可求得 ,进而可求得 ;
(2)法一:由正弦定理可得 , ,进而可得
,可求解.法二,利用余弦定理结合基本不等式可求得 的最大值,
进而可求解.
【详解】(1)因为 , ,三角形面积为 ,
所以 ,
,而 , ,
,所以需要修建多长的隔离防护栏 米.
(2)解法一:由(1)知 ,
设 , ,在 中,由正弦定理得:
,
所以 , ,
花卉观赏区的面积为:
因 ,则 ,
则当 ,即 时, 取值最大,
最大值 ,此时
故为了使花卉观赏区域的面积最大,应使观赏步道 米.
解法二:令 , ,由余弦定理得: ,
,,当且仅当 时取等号,
则最大值 ,
故为了使花卉观赏区域的面积最大,应使观赏步道 米.
19.(1)
(2)
(3)
【详解】(1)因为D为BC边的中点, .
所以 ,则 ,
所以 ,
所以 ,当且仅当 时取等号.
所以 .
(2)因为 ,D是BC边的中点,
,
, .
在 中,由余弦定理得: ,
, ,在 中,由正弦定理得: ,
;
(3)设 ,则 ,
在 中,由余弦定理得: ,
,
在 中,由余弦定理得: ,
,
,
在 中,由余弦定理得: ,
, , ,即 ,
, ,
所以 的取值范围为 .