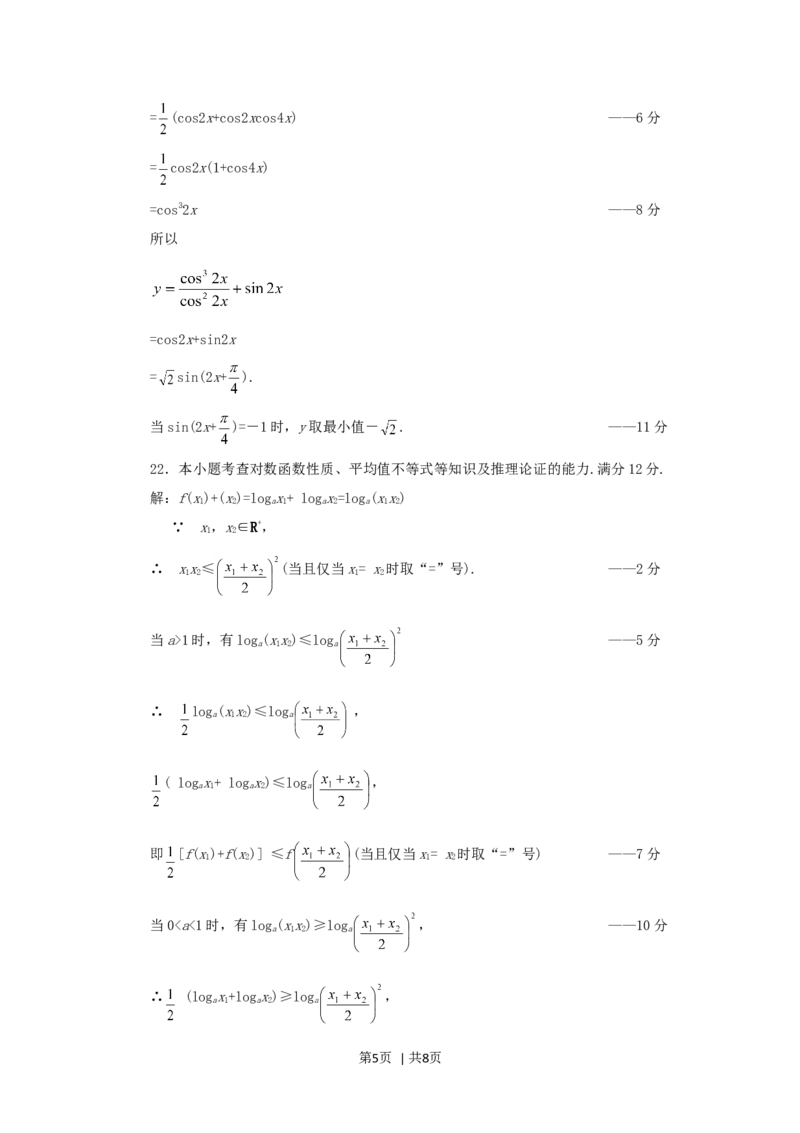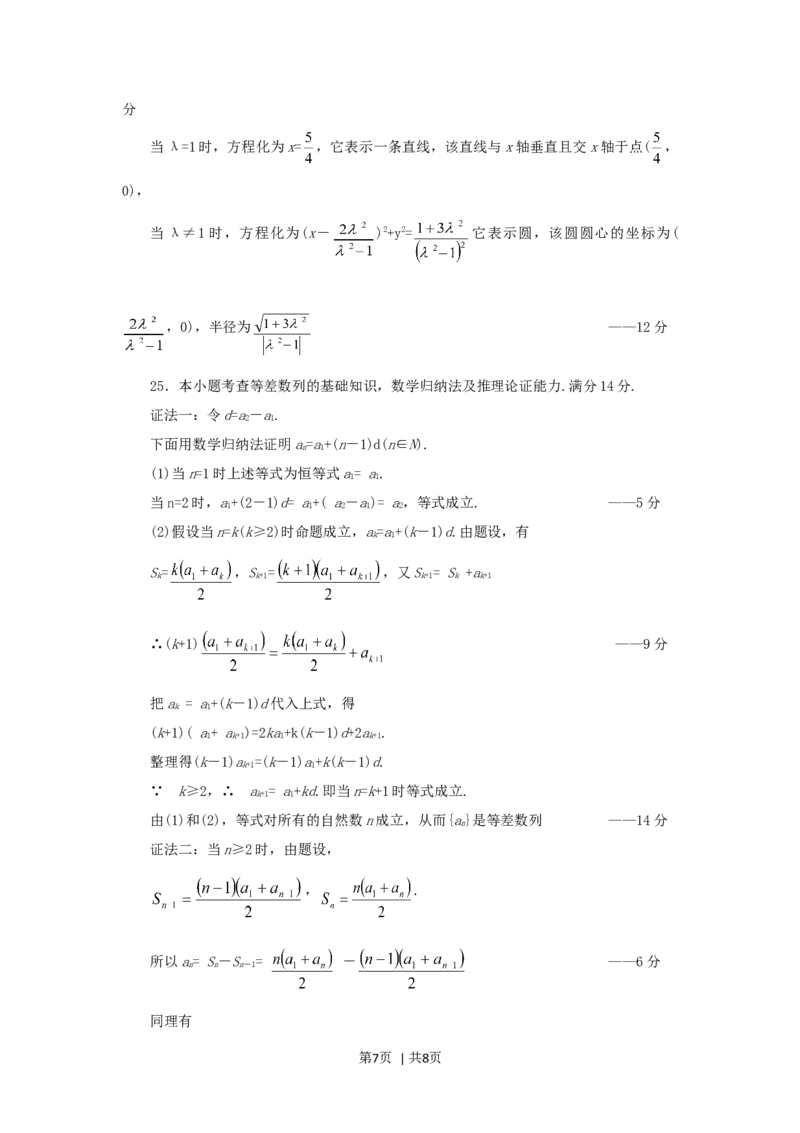文档内容
1994 年四川高考文科数学真题及答案
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.满分150分.考试时间120分钟.
第Ⅰ卷(选择题共65分)
一、选择题(本大题共15小题;第1—10题每小题4分,第11—15题每小题5分,共65
分.在每小题给出的四个选项中,只有一项是符合题目要求的)
王新奎新疆屯敞
(1) 设全集I={0,1,2,3,4},集合A={0,1,2,3},集合B={2,3,4},则
=
( )
(A) {0} (B) {0,1} (C) {0,1,4} (D) {0,1,2,3,
4}
(2) 如果方程x2+ky2=2表示焦点在y轴上的椭圆,那么实数k的取值范围是 ( )
(A) (0,+∞) (B) (0,2) (C) (1,+∞) (D) (0,1)
(3) 点(0,5)到直线y=2x的距离是 ( )
(A) (B) (C) (D)
(4) 设θ是第二象限的角,则必有 ( )
(A) (B)
(C) (D)
(5) 某种细菌在培养过程中,每20分钟分裂一次(一个分裂为两个).经过3个小时,
这种细菌由1个可繁殖成 ( )
(A) 511个 (B) 512个 (C) 1023个 (D) 1024个
(6) 在下列函数中,以 为周期的函数是 ( )
(A) (B) y=sin2xcos4x (C) (D) y=sin2xcos2x
y=sin2x+cos4x y=sin2x+cos2x
(7) 已知正六棱台的上,下底面边长分别为2和4,高为2,则其体积为 ( )
(A) 32 (B) 28 (C) 24 (D) 20
(8) 设F和F为双曲线 的两个焦点,点P在双曲线上且满足∠FPF=90º,
1 2 1 2
第1页 | 共8页则△FPF的面积是 ( )
1 2
(A) 1 (B) (C) 2 (D)
(9) 如果复数Z满足|Z+i|+|Z-i|=2,那么|Z+i+1|最小值是 ( )
(A) 1 (B) (C) 2 (D)
(10) 有甲、乙、丙三项任务,甲需2人承担,乙、丙各需1人承担,从10人中选派
4人承担这三项任务,不同的选法共有 ( )
(A) 1260种 (B) 2025种 (C) 2520种 (D) 5040种
(11) 对于直线m、n和平面α、β,α⊥β的一个充分条件是 ( )
(A) m⊥n,m∥α,n∥β (B) m⊥n,α∩β=m,n α
(C) m∥n,n⊥β,m α (D) m∥n,m⊥α,n⊥β
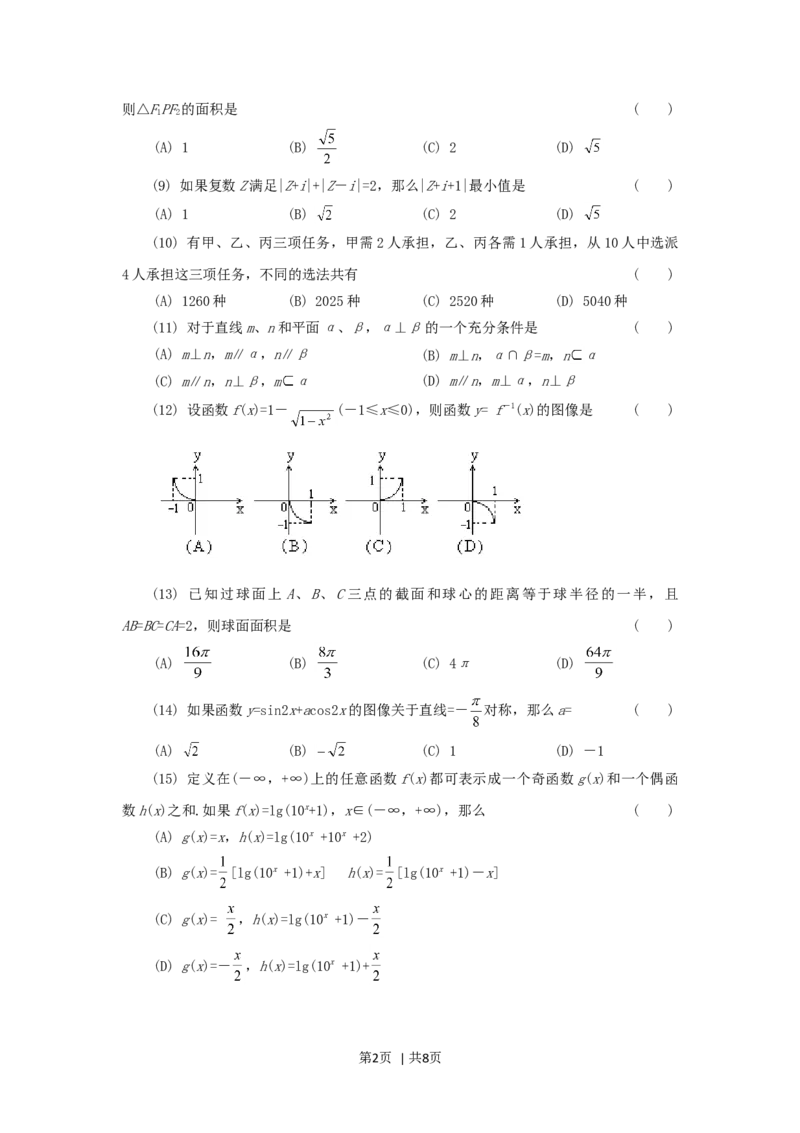
(12) 设函数f(x)=1- (-1≤x≤0),则函数y= f-1(x)的图像是 ( )
(13) 已知过球面上A、B、C三点的截面和球心的距离等于球半径的一半,且
AB=BC=CA=2,则球面面积是 ( )
(A) (B) (C) 4π (D)
(14) 如果函数y=sin2x+acos2x的图像关于直线=- 对称,那么a= ( )
(A) (B) (C) 1 (D) -1
(15) 定义在(-∞,+∞)上的任意函数f(x)都可表示成一个奇函数g(x)和一个偶函
数h(x)之和.如果f(x)=lg(10x+1),x∈(-∞,+∞),那么 ( )
(A) g(x)=x,h(x)=lg(10x +10x +2)
(B) g(x)= [lg(10x +1)+x] h(x)= [lg(10x +1)-x]
(C) g(x)= ,h(x)=lg(10x +1)-
(D) g(x)=- ,h(x)=lg(10x +1)+
第2页 | 共8页第Ⅱ卷(非选择题共85分)
二、填空题(本大题共5小题,共6个空格:每空格4分,共24分.把答案填在题中横线
上)
(16) 在(3-x)7的展开式中,x5的系数是______________(用数字作答)
王新奎新疆屯敞
(17) 抛物线y2=8-4x的准线方程是___________,圆心在该抛物线的顶点且与其准线
相切的圆的方程是__________
王新奎新疆屯敞
(18) 已知sinθ+cosθ= ,θ∈(0,π),则ctgθ的值是________________
王新奎新疆屯敞
(19) 设圆锥底面圆周上两点A、B间的距离为2,圆锥项点到直线AB的距离为 ,
AB和圆锥的轴的距离为1,则该圆锥的体积为____________
王新奎新疆屯敞
(20) 在测量某物理量的过程中,因仪器和观察的误差,使得n次测量分别得到a,
1
a,…,a,共n个数据.我们规定所测量的“量佳近似值”a是这样一个量:与其他近似
2 n
值比较,a与各数据的差的平方和最小.依此规定,从a,a,…,a推出的a=__________
1 2 n
王新奎新疆屯敞
三、解答题(本大题共5小题,共61分;解答应写出文字说明、证明过程或推演步骤)
(21) (本小题满分11分)
求函数 的最小值.
(22) (本小题满分12分)
以知函数f(x)=logx(a>0且a≠1,x∈R+),若x,x∈R+,判断 与
a 1 2
的大小,并加以证明.
(23) (本小题满分12分)
如图,已知ABC-ABC是正三棱柱,D是AC中点.
1 1 1
(1) 证明AB∥平面DBC;
1 1
(2) 假设AB⊥BC,BC=2,求线段AB在侧面BBCC上的射
1 1 1 1 1
影长.
第3页 | 共8页(24) (本小题满分12分)
已知直角坐标平面上点Q(2,0)和圆C:x2+y2=1,动点M到圆
C的切线长与|MQ|的比等于常数λ(λ>0).求动点M的轨迹方程,
说明它表示什么曲线.
(25)(本小题满分14分)
设数列{a}的前n项和为S,若对于所有的自然数n,都有 ,证明{a}
n n n
是等差数列.
参考答案
一、选择题(本题考查基本知识和基本运算)
1.C 2.D 3.B 4.A 5.B 6.D 7.B 8.A 9.A 10.C 11.C 12.B
13.D 14.D 15.C
二、填空题(本题考查基本知识和基本运算.每空格4分,共24分)
16.-189 17.x=3,(x-2)2+y2=1 18. 19.
20.
三、解答题
21.本小题考查利用有关三角公式并借助辅助角求三角函数最小值的方法及运算能力,
满分11分.
解:因为
sin3xsin3x+cos3xcos3x
=(sin3xsinx)sin2x+(cos3xcosx)cos2x
= [(cos2x-cos4x)sin2x+(cos2x+cos4x)cos2x] ——4分
= [(sin2x+cos2x)cos2x+(cos2x-sin2x)cos4x]
第4页 | 共8页= (cos2x+cos2xcos4x) ——6分
= cos2x(1+cos4x)
=cos32x ——8分
所以
=cos2x+sin2x
= sin(2x+ ).
当sin(2x+ )=-1时,y取最小值- . ——11分
22.本小题考查对数函数性质、平均值不等式等知识及推理论证的能力.满分12分.
解:f(x)+(x)=logx+ logx=log(xx)
1 2 a 1 a 2 a 1 2
∵ x,x∈R+,
1 2
∴ xx≤ (当且仅当x= x时取“=”号). ——2分
1 2 1 2
当a>1时,有log(xx)≤log ——5分
a 1 2 a
∴ log(xx)≤log ,
a 1 2 a
( logx+ logx)≤log ,
a 1 a 2 a
即 [f(x)+f(x)] ≤f (当且仅当x= x时取“=”号) ——7分
1 2 1 2
当00. ——2分
因为圆的半径|ON|=1,所以|MN|2=|MO|2-|ON|2=|MO|2-1. ——4分
设点M的坐标为(x,y),则 ——5分
整理得(λ2-1)(x2+y2 )-4λ2x+(1+4λ2)=0.
经检验,坐标适合这个方程的点都属于集合P.故这个方程为所求的轨迹方程. ——8
第6页 | 共8页分
当λ=1时,方程化为x= ,它表示一条直线,该直线与x轴垂直且交x轴于点( ,
0),
当λ≠1时,方程化为(x- )2+y2= 它表示圆,该圆圆心的坐标为(
,0),半径为 ——12分
25.本小题考查等差数列的基础知识,数学归纳法及推理论证能力.满分14分.
证法一:令d=a-a.
2 1
下面用数学归纳法证明a=a+(n-1)d(n∈N).
n 1
(1)当n=1时上述等式为恒等式a= a.
1 1
当n=2时,a+(2-1)d= a+( a-a)= a,等式成立. ——5分
1 1 2 1 2
(2)假设当n=k(k≥2)时命题成立,a=a+(k-1)d.由题设,有
k 1
S= ,S = ,又S = S +a
k k+1 k+1 k k+1
∴(k+1) ——9分
把a = a+(k-1)d代入上式,得
k 1
(k+1)( a+ a )=2ka+k(k-1)d+2a .
1 k+1 1 k+1
整理得(k-1)a =(k-1)a+k(k-1)d.
k+1 1
∵ k≥2,∴ a = a+kd.即当n=k+1时等式成立.
k+1 1
由(1)和(2),等式对所有的自然数n成立,从而{a}是等差数列 ——14分
n
证法二:当n≥2时,由题设,
, .
所以a= S-S = - ——6分
n n n-1
同理有
第7页 | 共8页a = - . ——8分
n+1
从而
a -a= -n(a+a)+ , ——12分
n+1 n 1 n
整理得 a -a= a-a =…= a-a
n+1 n n n-1 2 1
从而{a}是等差数列. ——14分
n
第8页 | 共8页