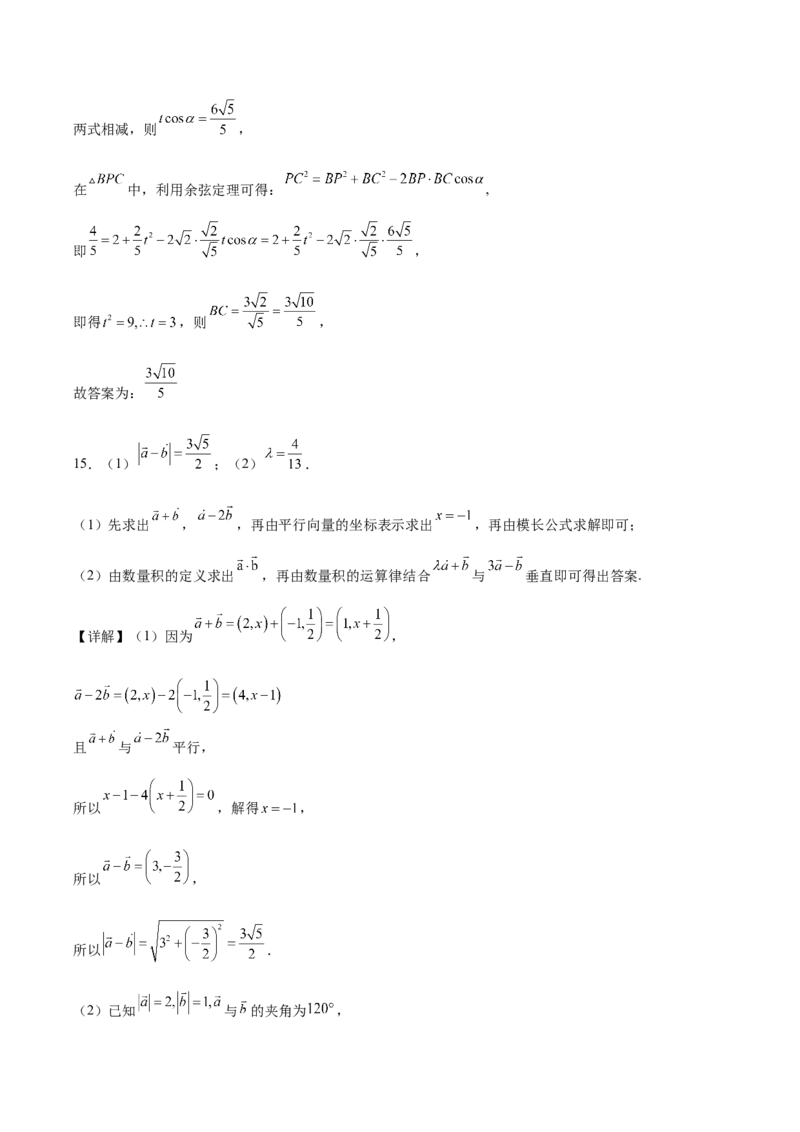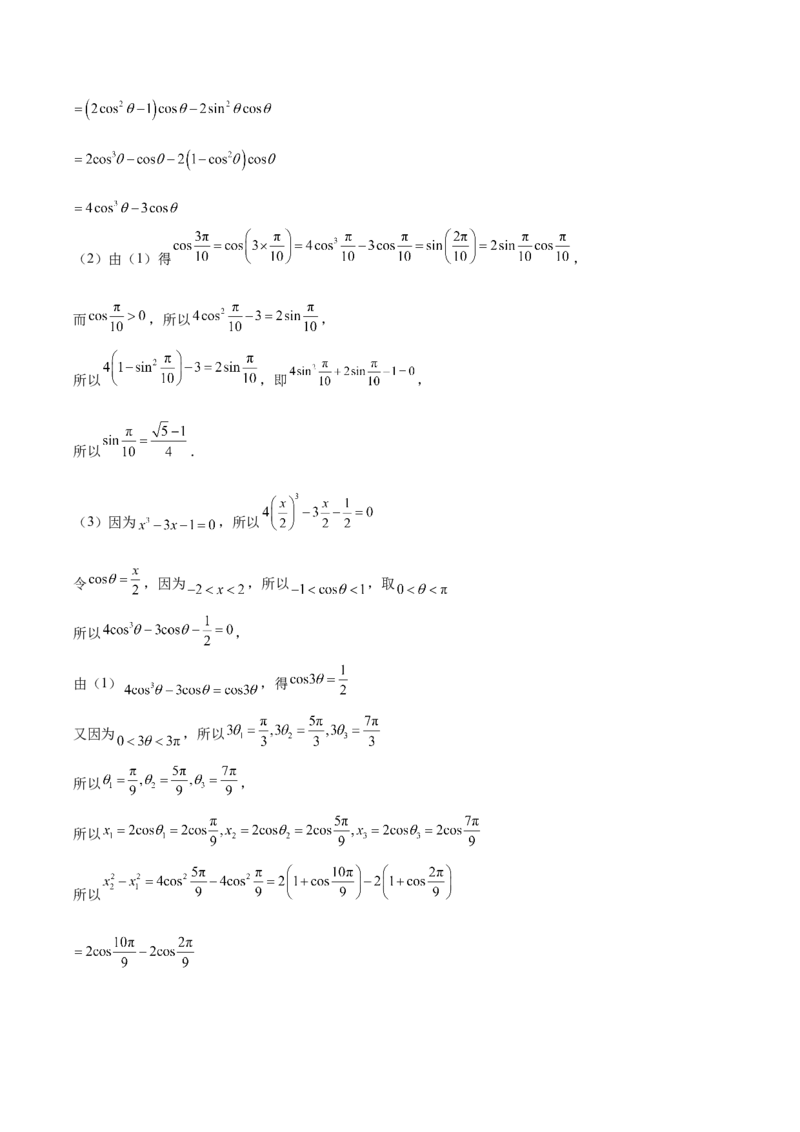文档内容
江苏省徐州市铜山区2024-2025学年高一下学期期中学情调研
数学试题
一、单选题
1. 的值为( )
A. B. C. D.
2.已知复数 满足 ,其中 是虚数单位,则复数 在复平面内对应的点位于
A.第一象限 B.第二象限
C.第三象限 D.第四象限
3.已知 与 是两个不共线的向量, ,若 三点共线,则
实数 的值为( )
A. B. C.4 D.5
4.在平行四边形 中, , ,则 ( )
A. B. C. D.
5.下列函数 的最小正周期为 的是( )
A. B.
C. D.
6.已知 ,函数 在 上有且只有一个零点,则 的取值范围是( )
A. B. C. D.
7.已知 为锐角, ,则 ( )A. B. C. D.
8.记 的面积为 ,角 的对边分别为 ,且 ,则 的形状是
( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.等边三角形
二、多选题
9.在复数范围内,下列命题正确的是( )
A.若 ,则 为纯虚数 B.若 ,则
C.若 ,则 的最大值为3 D.若 ,则
10.函数 ,则下列说法正确的是( )
A. 的图象关于点为 对称
B. 在区间 单调递增
C. 与 的图象有相同的对称轴
D. 与 的图象在 上有两个不同的交点
11.如图, 为边长为2的等边三角形,以 的中点 为圆心,1为半径作一个半圆,点 为此半圆
弧上的一个动点,则下列说法正确的是( )
A.B.
C. 的最大值为5
D.若 ,则当 三点共线时,
三、填空题
12.已知 是关于 的方程 的一个根,其中 为虚数单位,则 .
13.若 ,则 .
14.在等腰 中, ,在 内一点 满足 ,
则 的值为 .
四、解答题
15.(1)已知 ,若 与 平行,求 ;
(2)已知 与 的夹角为 ,若 与 垂直,求实数 的值.
16.已知 .
(1)求 的值;
(2)求 的大小.
17.已知 的内角 的对边分别为 ,且 .
(1)求 ;
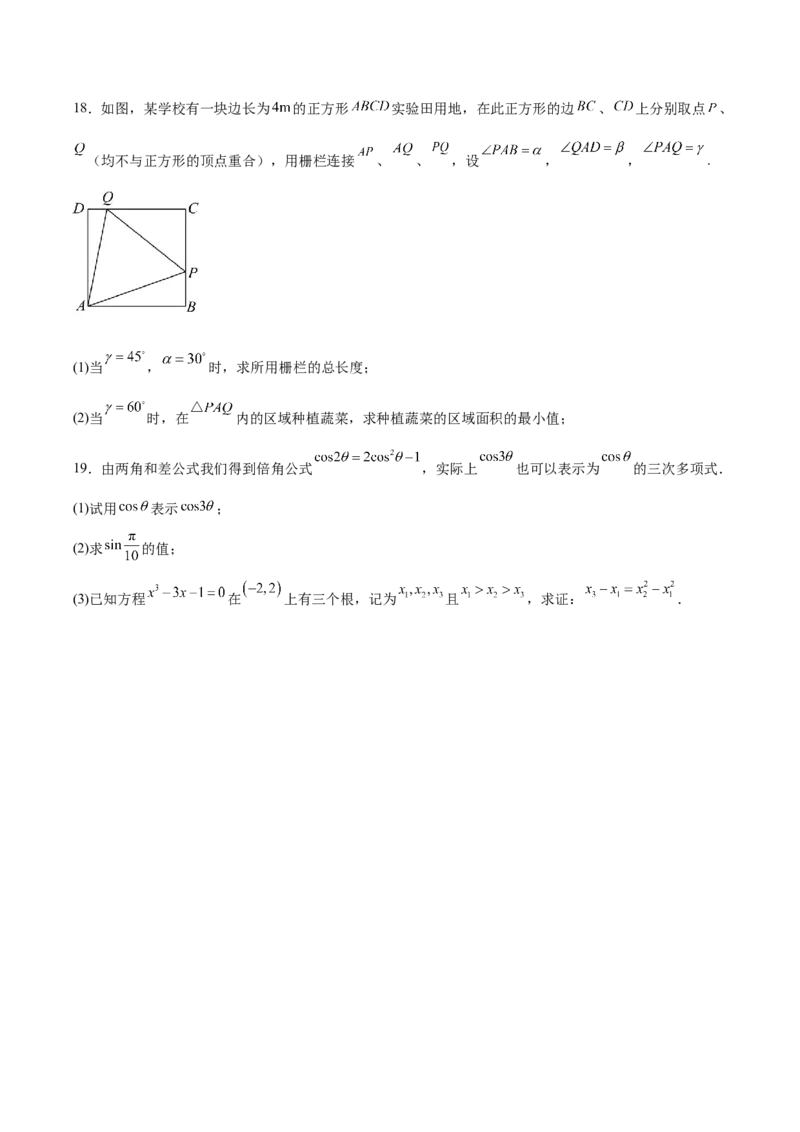
(2)若 , 的周长为9,点 是边 的中点,求线段 的长.18.如图,某学校有一块边长为 的正方形 实验田用地,在此正方形的边 、 上分别取点 、
(均不与正方形的顶点重合),用栅栏连接 、 、 ,设 , , .
(1)当 , 时,求所用栅栏的总长度;
(2)当 时,在 内的区域种植蔬菜,求种植蔬菜的区域面积的最小值;
19.由两角和差公式我们得到倍角公式 ,实际上 也可以表示为 的三次多项式.
(1)试用 表示 ;
(2)求 的值;
(3)已知方程 在 上有三个根,记为 且 ,求证: .题号 1 2 3 4 5 6 7 8 9 10
答案 D A B C C B D C BC ABD
题号 11
答案 ACD
1.D
由两角和的正弦公式求解即可.
【详解】
.
故选:D.
2.A
利用复数的除法运算法则:分子、分母同乘以分母的共轭复数,化简复数 ,从而得答案.
【详解】 ,
,
则在复平面内对应的点的坐标为 ,位于第一象限.
故选A.
3.B
【详解】因为 ,
所以 ,
因为 三点共线,必存在一个实数 ,使得 ,
所以 ,而 不共线,
所以 ,解得: .
故选:B.
4.C【详解】如下图所示:
在平行四边形 中, , ,则 , ,
故 .
故选:C.
5.C
利用三角恒等变换化简各选项中函数的解析式,再结合三角函数的周期公式逐项判断即可.
【详解】对于A选项, ,该函数的最小正周期为 ,A不满足要求;
对于B选项, ,
该函数的最小正周期为 ,B不满足要求;
对于C选项, ,
该函数的最小正周期为 ,C满足要求;
对于D选项, ,
该函数的最小正周期为 ,D不满足要求.
故选:C.
6.B
由 确定 ,根据正弦函数的零点列出相应不等式,即可求得答案.【详解】由 ,可得 ,
由于函数 在 上有且只有一个零点,
故 ,解得 ,
故选:B
7.D
利用同角三角函数关系求出 ,根据两角和正弦公式结合题意求出 ,继而求得
,再利用二倍角公式即可求得答案.
【详解】由于 为锐角,则
由 ,得 ,
即 ,结合 ,
可得 ,
故 ,
故 ,
故选:D
8.C
由余弦定理和三角形的面积公式可得 ,分别求出两部分的值域知
,即可知 的形状.【详解】由余弦定理可知: ,
所以 ,
所以 ,
所以 ,
因为 ,当且仅当 时取等,
又因为 的最大值为 ,
所以此时 ,
所以 ,此时 ,
所以 的形状是钝角三角形.
故选:C.
9.BC
取特值可判断AD;设 , ,由 可得 或 ,由此可判断B;由复数模的几何意
义可判断C.
【详解】对于A,若 ,设 , , ,
所以 ,
若 , ,则 ,不为纯虚数,故A错误;
对于B,设 , ,则 ,
若 ,则 , ,解得: ,即 或 ,所以 ,故B正确,
对于C, 表示复数 在复平面上对应的点到 的距离为 ,
即以 为圆心, 为半径的圆, 表示点 到原点的距离,
圆心 到原点的距离为 ,所以 的最大值为 ,故C正确;
对于D,取 , , , ,
满足 ,但 ,故D错误.
故选:BC.
10.ABD
计算 可判断A;求出 的单调递增区间可判断B;求出 与 的对称轴可判断
C;画出画出 与 在 的图象可判断D.
【详解】对于A,因为 ,
故 的图象关于点为 对称,故A正确;
对于B,令 , ,
所以 , ,
令 ,则 ,而 ,故B正确;
对于C,令 ,解得: ,
的对称轴为 ,令 ,解得: ,
的对称轴为 ,
令 ,则 ,
则 ,故 与 的图象没有相同的对称轴,故C错误;
对于D,画出 与 在 的图象,如下图,
可知 与 的图象在 上有两个不同的交点,故D正确.
令
故选:ABD.
11.ACD
由向量的线性运算可判断A;由数量积的定义可判断B;以 为坐标原点,建立平面直角坐标系,结合三
角函数的性质可判断C;由共线向量定理求出 可判断D.
【详解】对于A, ,故A正确;
对于B,由A知, ,
,故B错误;
对于C,以 为坐标原点,建立如图所示的平面直角坐标系,
, ,设 ,
所以 ,当 时, 的最大值为5,故C正确;
对于D,当 三点共线时, ,
,所以 ,
又因为 ,所以 ,
所以 ,所以 ,故D正确.
故选:ACD.
12.1
确定方程的另外一根,根据韦达定理即可求得答案.
【详解】由题意知 是关于 的方程 的一个根,
则 是该方程的另一个根,则 ,
即 ,则 ,
故答案为:1
13.
利用二倍角的正弦、余弦公式结合弦化切可得出所求代数式的值.
【详解】 .
故答案为: .14. /
利用余弦定理求出 ,继而利用三角形相似求出 ,设 ,
,在 和 中,利用余弦定理求出 ,在 中,利用
余弦定理即可求出t的值,即可求得答案.
【详解】在等腰 中, ,
则 ,
即 ,设 ,则 ;
,结合 知 ,
可得 ,则 ∽ ,
故 ,而 , ,
故 ,
设 ,在 和 中,利用余弦定理可得:
, ,
即 , ,两式相减,则 ,
在 中,利用余弦定理可得: ,
即 ,
即得 ,则 ,
故答案为:
15.(1) ;(2) .
(1)先求出 , ,再由平行向量的坐标表示求出 ,再由模长公式求解即可;
(2)由数量积的定义求出 ,再由数量积的运算律结合 与 垂直即可得出答案.
【详解】(1)因为 ,
且 与 平行,
所以 ,解得 ,
所以 ,
所以 .
(2)已知 与 的夹角为 ,所以 ,
因为 与 垂直,
所以
所以 .
16.(1)
(2) .
(1)由同角三角函数的基本关系求出 、 ,从而求出 、 ,再由两角和的正弦公式计
算可得;
(2)首先求出 ,再由 及两角和的正弦公式计算可得.
【详解】(1)因为 ,所以 ,解得 (负值舍去);
所以 ,
所以 .
(2)因为 ,所以 ,
又因为 ,所以 ,
所以,
又因为 ,所以 .
17.(1) .
(2) .
(1)由正弦定理结合两角和的正弦定理可得 ,即可求出答案;
(2)由点 是 的中点可得 ,对其两边平方则 ,再由余弦定理
可得 ,两式联立结合 的周长,即可求出 ,进而求出线段 的长.
【详解】(1)因为 ,
由正弦定理得
所以 ,即 ,
又因为 ,所以 .
(2)因为点 是 的中点,所以 ,
所以
在 中 ,
由余弦定理得 ,
所以 ,
所以
又因为 的周长为 ,所以
所以 ,所以 ,所以 ,
所以 ,所以 .18.(1) 米
(2) 平方米
(1)在 、 中,分别求出 、 的长,然后在 中利用余弦定理求出 的长,
可求出 的周长,即为所求;
(2)求得 , ,利用三角形的面积公式得出 ,利用三角恒等变换
结合正弦型函数的基本性质求出 的最大值,即可得出 面积的最小值.
【详解】(1)因为 , ,则 ,
在 中, ,
因为 ,
在 中, ,
所以在 中由余弦定理得
所以 ,
所以 ,
所以栅栏总长度为 米.(2)在 中, ,在 中, ,
所以 的面积 ,
,
因为 ,所以 ,
当 即 时, 取得最大值 ,
此时 的面积的最小值为 ,
所以植蔬菜的区域面积的最小值为 平方米.
19.(1)
(2) .
(3)证明见解析
(1)利用二倍角的正弦和余弦公式可证明三倍角公式;
(2)利用(1)的结果可得 ,故可求 的值;
(3)令 ,结合(1)中恒等式对方程变形可得 ,故可求原方程的解,结合三角变换公式
可证 .
【详解】(1)(2)由(1)得 ,
而 ,所以 ,
所以 ,即 ,
所以 .
(3)因为 ,所以
令 ,因为 ,所以 ,取
所以 ,
由(1) ,得
又因为 ,所以
所以 ,
所以
所以.
故 .