文档内容
2024-2025 学年江苏省徐州市沛县高一下学期第一次学情调研
数学试卷
一、单选题:本题共8小题,每小题5分,共40分。在每小题给出的选项中,只有一项是符合题目要求的。
1.化简cos43∘cos13∘+sin43∘sin13∘,得( )
1 √2 √3
A. B. C. D. cos56∘
2 2 2
2.已知向量→ →的夹角为 ,且 → → ,则→ → ( )
60°
a,b |a|=1,|b|=2 a⋅b=
1 √3
A. B. C. 1 D. 2
2 2
3.已知四边形ABCD的三个顶点A(0,2),B(−1,−2),C(3,1),且⃗BC=2⃗AD,则顶点D的坐标为( )
7 1
A. (2, ) B. (2,− ) C. (3,2) D. (1,3)
2 2
4.已知 4, ( π ), 1,则 的值为( )
cosα= α∈ − ,0 tanβ= tan(α−β)
5 2 2
2 10 2
A. − B. − C. − D. −2
5 11 11
5.已知⃗ e , ⃗ e 是两个不共线的向量⃗ a= ⃗ e +3 ⃗ e , ⃗ b=−2 ⃗ e +k ⃗ e ,若 ⃗a 与 ⃗b 是共线向量,则实数 k 的值为( )
1 2 1 2 1 2
3 3
A. −6 B. 6 C. D. −
2 2
6.已知 分别是 的边 的中点,且 , , ⃗ ⃗,则下列结论中错
D、E、F ▵ABC BC、CA、AB ⃗BC=⃗a ⃗CA=⃗b
AB=c
误的是( )
⃗ 1⃗ 1⃗
A. EF= c+ b B. ⃗ ⃗ ⃗ ⃗
AB+AC+BC=0
2 2
⃗ 1⃗ 1⃗
C. CF=− a+ b D. ⃗ ⃗ ⃗ ⃗
AD+BE+CF=0
2 2
π π 4
7.已知 <α<π,且cos(α− )=− ,则cosα的值为( )
2 6 5
3 4 3−4√3
A. B. − C. D.
5 5 10
第 页,共 页
1 18.矩形 ABCD 中, AB=√2 , AD=1 , M 是矩形 ABCD 内 ( 不含边框 ) 的动点, |M ⃗ A|=1 ,则 M ⃗ C⋅M ⃗ D 的
最小值为( )
3+√6
A. −√6 B. −√6+1 C. −√6+2 D.
2
二、多选题:本题共3小题,共18分。在每小题给出的选项中,有多项符合题目要求。
9.设⃗a,⃗b,⃗c是任意的非零向量,且它们相互不共线,给出下列选项,其中正确的有( )
A. ⃗ ⃗ ⃗ ⃗ (⃗ ⃗) ⃗
a⋅c−b⋅c= a−b ⋅c
B. 若⃗ ⃗ ⃗ ⃗且⃗ ,则⃗ ⃗
a⋅c=b⋅c c≠0 a=b
C. |⃗| |⃗| |⃗ ⃗|
a − b < a−b
2 2
D. ( ⃗ ⃗) ( ⃗ ⃗) |⃗| |⃗|
3a+2b ⋅3a−2b =9 a −4 b
10.下列计算中正确的是( )
A. tanx+tan y sin(x+ y)
=
tanx−tan y sin(x−y)
B. sin(α+β)cosα+cosβ
√5 √10 √2
D. α,β都是锐角,cosα= ,sin(α−β)= ,则cosβ=
5 10 2
11.下列关于平面向量的说法中正确的是( )
A. 若 ⃗a,⃗b,⃗c 为非零向量,则(⃗
b⋅
⃗
c
)
⋅
⃗
a−
(⃗
c⋅
⃗
a
)
⋅
⃗
b
不与 ⃗c 垂直
B. 、 为实数,若 ⃗ ⃗,则 与 共线
λ μ
λa=μb
⃗a ⃗b
第 页,共 页
2 1C. 若平面内有四个点 ,则必有 ⃗ ⃗ ⃗ ⃗
A,B,C,D
AC+BD=BC+AD
⃗ ⃗
AB AC ⃗
D. 在▵ABC中,D为BC的中点,若 + =λAD,则⃗BD是⃗BA在⃗BC上的投影向量
| ⃗ | | ⃗ |
AB AC
三、填空题:本题共3小题,每小题5分,共15分。
12.计算: √3−tan15∘ .
=
1+√3tan15∘
13.设
λ
为实数,已知
⃗e
为单位向量,向量
⃗a
的模为
2
,⃗
a=λ
⃗
e
,
λ=
.
14.圆是中华民族传统文化的形态象征,象征着“圆满”和“饱满”,是自古以和为贵的中国人所崇尚的
图腾.AB是圆O的一条直径,且|AB|=4.C,D是圆O上的任意两点,|CD|=2,点P在线段CD上,则
⃗PA⋅⃗PB的取值范围是 .
四、解答题:本题共5小题,共77分。解答应写出文字说明,证明过程或演算步骤。
15.(本小题13分)
如图,在▱ABCD中,AB=2,AD=1,∠BAD=60∘.求:
⃗ ⃗
(1)AB⋅AC的值;(2)cos∠BAC.
16.(本小题15分)
已知点A(2,3),B(4,−1),C(−2,1),求:
⃗ ⃗ 的值;
(1)CA⋅CB
(2)∠ACB的大小;
(3)点A到直线BC的距离.
第 页,共 页
3 117.(本小题15分)
已知向量⃗ ⃗ ,其中 (π ),且 ⃗ ⃗ .
m=(sinα,−1),n=(−3,cosα)
α∈
2
,π
m⊥n
(1)求tanα,sinα,cosα的值;
若 √5,且 ( π),求角 的值.
(2) sin(α+β)=− β∈ 0, β
5 2
18.(本小题17分)
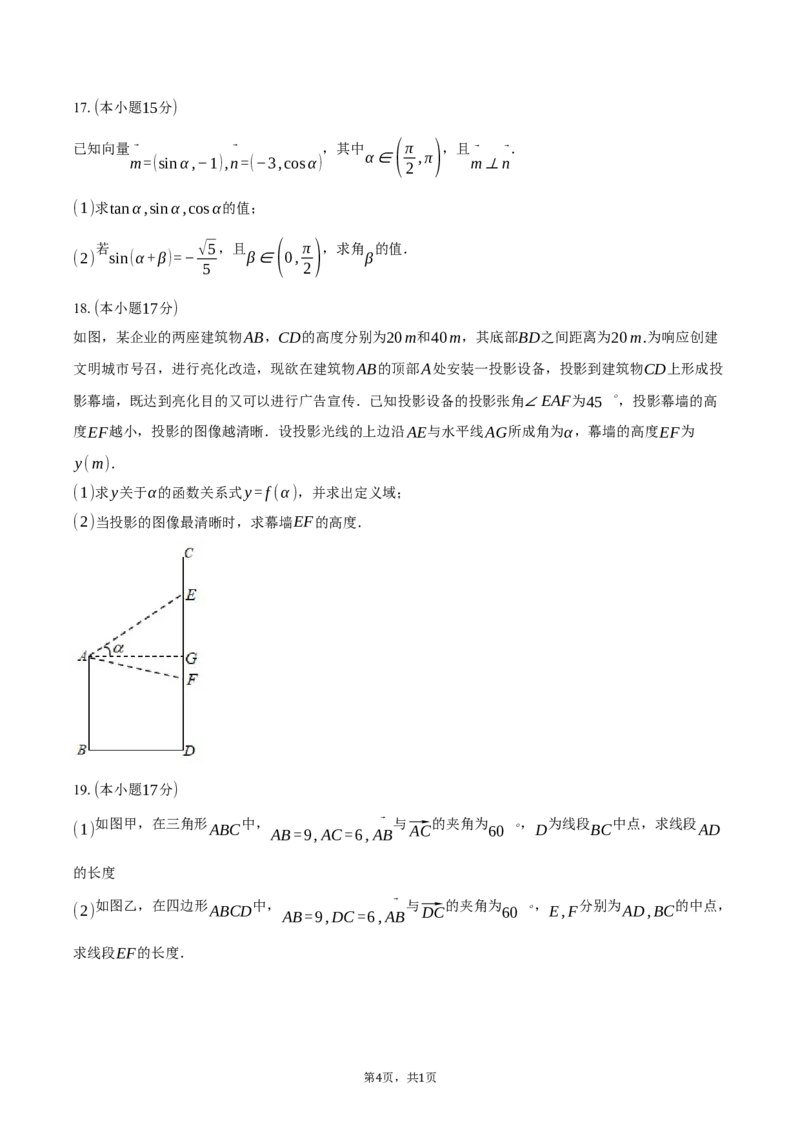
如图,某企业的两座建筑物AB,CD的高度分别为20m和40m,其底部BD之间距离为20m.为响应创建
文明城市号召,进行亮化改造,现欲在建筑物AB的顶部A处安装一投影设备,投影到建筑物CD上形成投
影幕墙,既达到亮化目的又可以进行广告宣传.已知投影设备的投影张角∠EAF为45 ∘,投影幕墙的高
度EF越小,投影的图像越清晰.设投影光线的上边沿AE与水平线AG所成角为α,幕墙的高度EF为
y(m).
(1)求y关于α的函数关系式y=f(α),并求出定义域;
(2)当投影的图像最清晰时,求幕墙EF的高度.
19.(本小题17分)
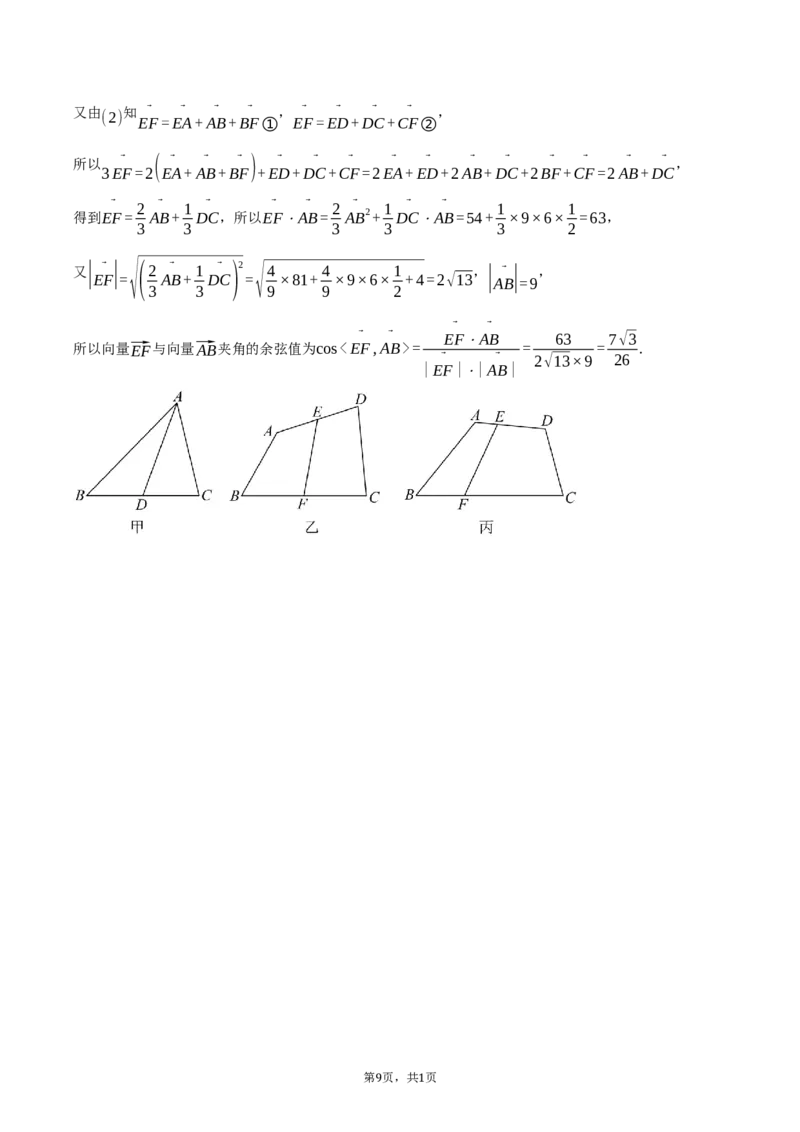
如图甲,在三角形 中, ⃗ 与 的夹角为 , 为线段 中点,求线段
(1) ABC AB=9,AC=6,AB ⃗AC 60 ∘ D BC AD
的长度
如图乙,在四边形 中, ⃗ 与 的夹角为 , 分别为 的中点,
(2) ABCD AB=9,DC=6,AB ⃗DC 60 ∘ E,F AD,BC
求线段EF的长度.
第 页,共 页
4 1如图丙,在四边形中, 分别在边 上,且 ⃗ ⃗ ⃗ ⃗ ⃗ 与
(3) E,F AD,BC
AD=3AE,BC=3BF,AB=9,DC=6,AB
⃗DC的夹角为60 ∘,求向量⃗EF与向量⃗AB夹角的余弦值.
第 页,共 页
5 1参考答案
1.C
2.C
3.A
4.D
5.A
6.B
7.D
8.C
9.ACD
10.AD
11.CD
12.1
13.±2
14.[−1,0]
15.解:(1)由题意,在□ ABCD中,AB=2,AD=1,∠BAD=60°,
所以 ⃗ ⃗ ⃗ ⃗ ⃗ ⃗ ⃗ ⃗ ;
AB⋅AC=AB⋅(AB+AD)=AB2+AB⋅AD=4+2×1×cos60∘=5
⃗ ⃗ ⃗ √ ⃗ ⃗ √ ⃗ ⃗ ⃗ ⃗ ,
(2)|AC|=|AB+AD|= (AB+AD) 2= AB2+2AB⋅AD+AD2=√7
→ →
AB·AC 5 5√7
cos∠BAC= = = .
→ → 2×√7 14
|AB|·|AC|
16.解:依题意,得: ⃗ ,
CA=(2,3)−(−2,1)=(4,2)
⃗ ,
CB=(4,−1)−(−2,1)=(6,−2)
⃗ ⃗ ;
(1)CA⋅CB=4×6+2×(−2)=20
⃗ ⃗
CA⋅CB 20 √2
(2)因为cos∠ACB= = =
,
| ⃗ || ⃗ | √20×√40 2
CA CB
第 页,共 页
6 1π
又0⩽∠ACB⩽π,所以∠ACB= ;
4
(3)点A到直线BC的距离为
⃗ √2
d=|CA|sin∠ACB=√20× =√10.
2
1
17.(1)因为⃗ ⃗,所以−3sinα−cosα=0,即tanα=− ,
m⊥n
3
sinα 1 1
又tanα= =− ,得到cosα=−3sinα,代入sin2α+cos2α=1,得到sin2α= ,
cosα 3 10
又 (π ),所以 √10 3√10.
α∈ ,π sinα= ,cosα=−
2 10 10
√10 3√10
(2)由(1)得sinα= ,cosα=− ,
10 10
,
sinβ=sin[(α+β)−α]=sin(α+β)cosα−cos(α+β)sinα
因为 (π ), ( π),所以 (π 3π),
α∈ ,π β∈ 0, α+β∈ ,
2 2 2 2
因为 √5,所以 ( 3π), 2√5,
sin(α+β)=− α+β∈ π, cos(α+β)=−
5 2 5
所以 √5 ( 3√10) ( 2√5) √10 √2,
sinβ=sin(α+β)cosα−cos(α+β)sinα=− × − − − × =
5 10 5 10 2
π
所以β= .
4
18.(1)由AB=20m,CD=40m,BD=20m可得,∠CAG=45 ∘,∠GAD=45 ∘,
又投影设备的投影张角 为 ,所以 [ π],
∠EAF 45 ∘ α∈ 0,
4
所以G一定在EF上,所以EF=EG+GF,
所以 (π ) [ π].
y=20tanα+20tan −α ,α∈ 0,
4 4
第 页,共 页
7 1(2)当投影的图像最清晰时,幕墙EF的高度最小,即求y的最小值
由 得 (π ) [ π]
(1) y=20tanα+20tan −α ,α∈ 0,
4 4
( 1−tanα) [ 2 ],
=20 tanα+ =20 (tanα+1)+ −2
1+tanα 1+tanα
因为 [ π],所以 ,
α∈ 0, tanα∈[0,1],tanα+1>0
4
2
所以(tanα+1)+ ≥2√2,
1+tanα
2
当且仅当tanα+1= ,即tanα=√2−1时取等号,
1+tanα
又tanα=√2−1∈[0,1],所以满足题意,
此时, .
y =40(√2−1)
min
答:当 时,投影的图像最清晰,此时幕墙 的高度为
tanα=√2−1 EF 40(√2−1)m.
⃗ 1( ⃗ ⃗ ) ⃗ 1( ⃗ ⃗ ⃗ ⃗ )
19.(1)因为AD= AB+AC ,所以AD2= AB2+2AB⋅AC+AC2 ,
2 4
又 AB=9,AC=6,A ⃗ B 与 ⃗AC 的夹角为 60 ∘ ,所以 A ⃗ D2= 1( 81+2×9×6× 1 +36 ) = 171,
4 2 4
| ⃗ | √171
故 AD = .
2
因为 ⃗ ⃗ ⃗ ⃗ , ⃗ ⃗ ⃗ ⃗ ,
(2)
EF=EA+AB+BF① EF=ED+DC+CF②
由 ①+② 得 2E ⃗ F=A ⃗ B+D ⃗ C ,所以 4E ⃗ F2=A ⃗ B2+2A ⃗ B⋅D ⃗ C+D ⃗ C2 ,
⃗ 1
又
AB=9,DC=6,A
⃗
B
与⃗DC的夹角为60 ∘,所以4EF2=81+2×9×6× +36=171,
2
| ⃗ | √171
得到 EF = .
2
因为 ⃗ ⃗ ⃗ ⃗ ⃗ 与 的夹角为 ,
(3) AD=3AE,BC=3BF,AB=9,DC=6,AB ⃗DC 60 ∘
第 页,共 页
8 1又由 知 ⃗ ⃗ ⃗ ⃗ , ⃗ ⃗ ⃗ ⃗ ,
(2)
EF=EA+AB+BF① EF=ED+DC+CF②
所以 ⃗ ( ⃗ ⃗ ⃗ ) ⃗ ⃗ ⃗ ⃗ ⃗ ⃗ ⃗ ⃗ ⃗ ⃗ ⃗ ,
3EF=2 EA+AB+BF +ED+DC+CF=2EA+ED+2AB+DC+2BF+CF=2AB+DC
⃗ 2 ⃗ 1 ⃗ ⃗ ⃗ 2 ⃗ 1 ⃗ ⃗ 1 1
得到EF= AB+ DC,所以EF⋅AB= AB2+ DC⋅AB=54+ ×9×6× =63,
3 3 3 3 3 2
又| ⃗ | √ (2 ⃗ 1 ⃗ ) 2 √4 4 1 ,| ⃗ | ,
EF = AB+ DC = ×81+ ×9×6× +4=2√13 AB =9
3 3 9 9 2
⃗ ⃗
⃗ ⃗ EF⋅AB 63 7√3
所以向量⃗EF与向量⃗AB夹角的余弦值为cos= = = .
⃗ ⃗ 2√13×9 26
|EF|⋅|AB|
第 页,共 页
9 1