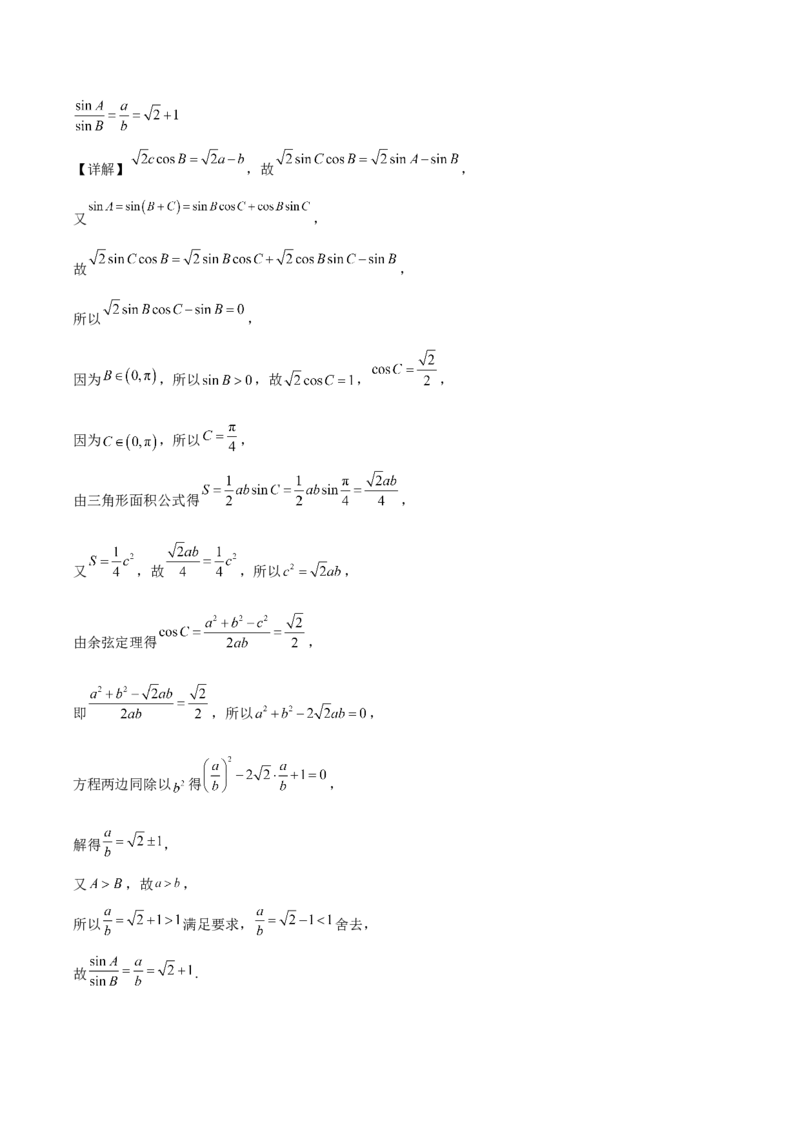文档内容
2024-2025学年高一下学期4月
期中学业水平质量监测数学试题(A)
一、单选题
1.设 ,若向量 , ,且 ,则m的值为( )
A. B. C.4 D.9
2.设复数 , ( ).若 为实数,则 ( )
A. B.2 C. D.4
3.在 中,若 ,则 的形状是( )
A.等腰三角形 B.直角三角形 C.等腰或直角三角形D.等边三角形
4.在 中,C是AB上一点,且 ,若 ,则实数 的值为( )
A. B. C.1 D.2
5.已知 , ,则 ( )
A. B. C. D.
6.已知非零向量 在向量 上的投影向量为 , ,则 ( )
A. B. C. D.
7.已知向量 , ,若 ,则 ( )
A. B. C. D.
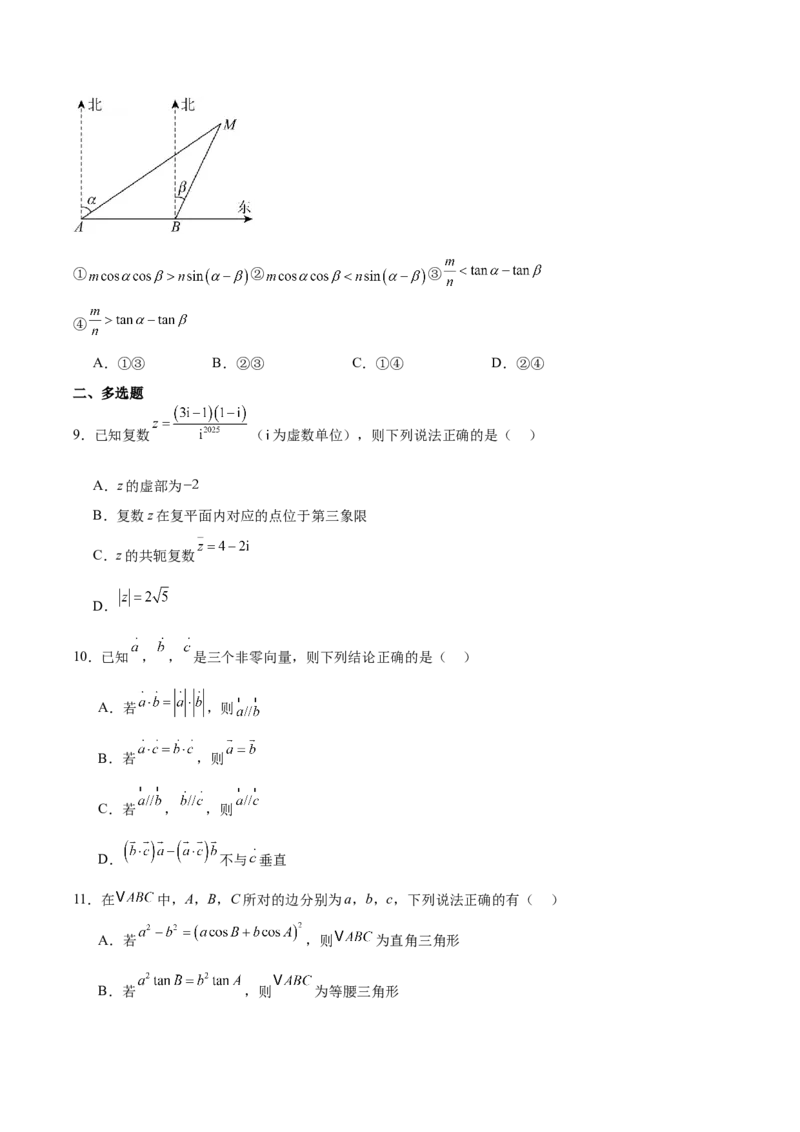
8.一船在海上自西向东航行,在A处测得某岛M的方位角为北偏东 ,前进m千米后在B处测得该岛的
方位角为北偏东 ,已知该岛周围n千米范围内(包括边界)有暗礁,现该船继续东行,若该船没有触礁
危险,则 , 满足的条件为( )① ② ③
④
A.①③ B.②③ C.①④ D.②④
二、多选题
9.已知复数 ( 为虚数单位),则下列说法正确的是( )
A.z的虚部为
B.复数z在复平面内对应的点位于第三象限
C.z的共轭复数
D.
10.已知 , , 是三个非零向量,则下列结论正确的是( )
A.若 ,则
B.若 ,则
C.若 , ,则
D. 不与 垂直
11.在 中,A,B,C所对的边分别为a,b,c,下列说法正确的有( )
A.若 ,则 为直角三角形
B.若 ,则 为等腰三角形C.若 ,则
D.若 是锐角三角形,则
三、填空题
12.在 中,已知 , , ,则 = .
13.已知 ,则 .
14.在 中,a,b,c分别为角A,B,C的对边, 的面积 ,若 且
,则 .
四、解答题
15.已知向量 , , .
(1)求 ;
(2)求 与 的夹角 .
16.已知复数 ( )
(1)若 ,求实数m的值;
(2)若z为虚数,求实数m的取值范围;
(3)若复数z对应的点在第四象限,求实数m的取值范围.
17.定义向量 的“伴随函数”为 ,函数 的“伴随向
量”为 .
(1)写出向量 的伴随函数 ,并直接写出 的最大值M;
(2)求函数 的伴随向量 的模.
18.在 中,A,B,C的对边分别为a,b,c,已知 .
(1)求证: ;(2)若D为BC的中点, , ,求AD的长.
19.在非直角三角形ABC中,边长a,b,c满足 ( ,且 )
(1)若 ,且 ,求 的值;
(2)求证: ;
(3)是否存在函数 ,使得对于一切满足条件的 ,代数式 恒为定值?若存在,请给
出一个满足条件的 ,并证明,若不存在,请给出一个理由.题号 1 2 3 4 5 6 7 8 9 10
答案 D B A D B C B C AD AC
题号 11
答案 ACD
1.D
根据向量平行得到方程,求出答案.
【详解】由题意得 ,解得 .
故选:D
2.B
利用复数除法法则化简,得到 ,解得 .
【详解】 ,
为实数,故 ,解得 .
故选:B
3.A
由正弦定理把已知的等式化边为角,结合两角和的正弦化简,求出 ,进一步求得 ,即可
得解.
【详解】解:由 ,结合正弦定理可得: ,
,可得: ,
,则 的形状为等腰三角形.
故选: .
4.D
变形得到 ,故 ,得到答案.
【详解】 ,
所以 ,故 .
故选:D
5.B由余弦和差公式得到方程,求出 ,利用同角三角函数关系得到答案.
【详解】 ,
,
联立可得 ,
所以 .
故选:B
6.C
利用投影向量的公式得到方程,求出 ,从而利用向量数量积运算法则得到答案.
【详解】 在向量 上的投影向量为 ,故 ,
所以 ,
又 ,所以 ,
所以 .
故选:C
7.B
由 求得 ,再用倍角公式求 即可.
【详解】因为 , , ,
所以 ,即 ,
所以 ,解得 或 (舍),所以 ,
故选:B
8.C
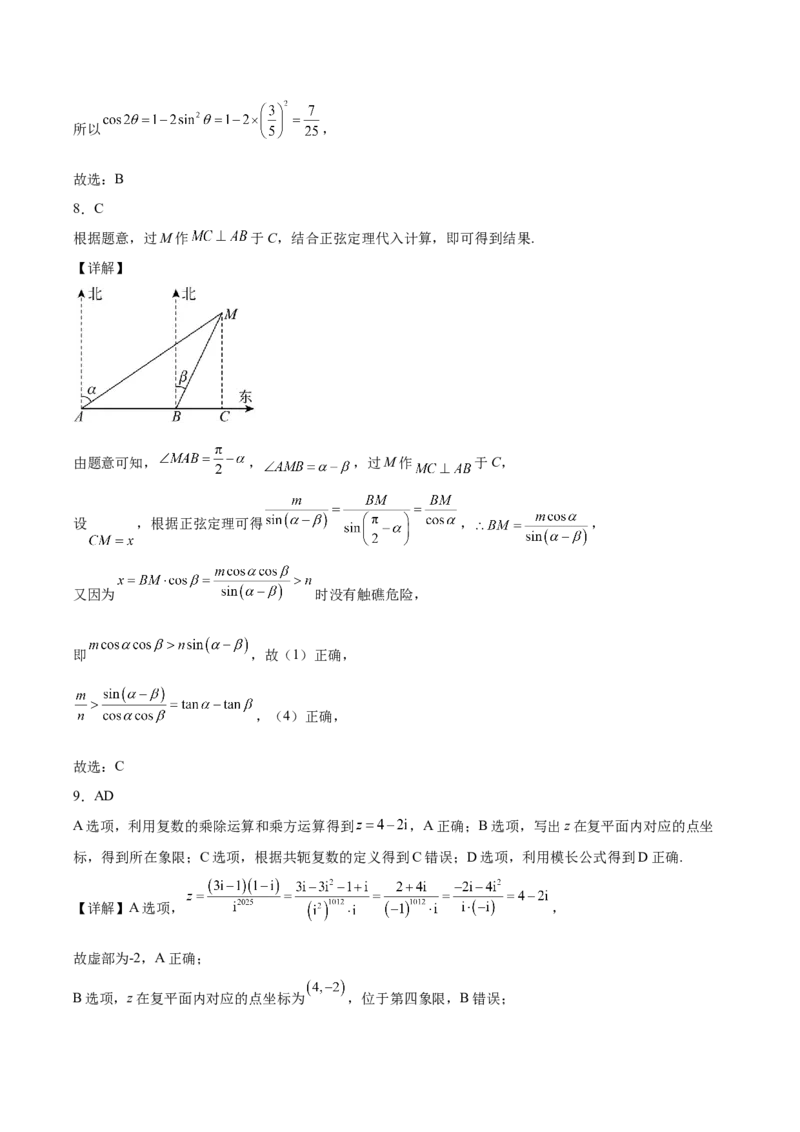
根据题意,过M作 于C,结合正弦定理代入计算,即可得到结果.
【详解】
由题意可知, , ,过M作 于C,
设 ,根据正弦定理可得 , ,
又因为 时没有触礁危险,
即 ,故(1)正确,
,(4)正确,
故选:C
9.AD
A选项,利用复数的乘除运算和乘方运算得到 ,A正确;B选项,写出z在复平面内对应的点坐
标,得到所在象限;C选项,根据共轭复数的定义得到C错误;D选项,利用模长公式得到D正确.
【详解】A选项, ,
故虚部为-2,A正确;
B选项,z在复平面内对应的点坐标为 ,位于第四象限,B错误;C选项,z的共轭复数 ,C错误;
D选项, ,D正确.
故选:AD
10.AC
A选项,利用向量数量积公式得到 ,所以 同向共线,A正确;B选项,只能得到
,B错误;C选项,得到 , ,C正确;D选项,计算出
,故D错误.
【详解】A选项, ,又 , , 是非零向量,
所以 ,所以 同向共线,A正确;
B选项,若 ,则 ,
是非零向量,故 ,故 不一定相等,B错误;
C选项,若 , ,设 ,
故 , ,C正确;
D选项, ,
与 垂直,D错误.
故选:AC
11.ACD
A选项,由正弦定理得到 ,从而 ,得到A正确;B选项,由同角三角函数关
系,正弦定理和二倍角公式得到 ,所以 或 ,B错误;C选项,由大角对大边得到 ,由正弦定理得到 ;D选项,根据锐角三角形得到 ,结合正弦函数单调
性和诱导公式比较出大小
【详解】A选项,由正弦定理得 ,
故 ,
故
,
所以 ,即 ,
则 为直角三角形,A正确;
B选项,若 ,则 ,
由正弦定理得 ,
又 ,故 ,
所以 ,即 , ,
所以 或 ,所以 或 ,
为等腰三角形或直角三角形,B错误;
C选项,若 ,则 ,
由正弦定理得 ,又 , ,
故 ,C正确;
D选项,若 是锐角三角形,则 ,则 ,
其中 , ,
又 在 上单调递增,故 ,故D正确.
故选:ACD
12. 或 .
利用正弦定理计算即可.
【详解】由 ,且根据正弦定理可知 ,
因为 ,所以 或 .
故答案为: 或 .
13.
由 得到 ,由两角和差余弦公式展开化简即可求解;
【详解】由 ,
得: ,
,
,
所以 ,
故答案为:
14.
由正弦定理和 化简得到 ,求出 ,由三角形面积公式得到
,由余弦定理得到方程,求出 ,舍去不合要求 的解,由正弦定理得到【详解】 ,故 ,
又 ,
故 ,
所以 ,
因为 ,所以 ,故 , ,
因为 ,所以 ,
由三角形面积公式得 ,
又 ,故 ,所以 ,
由余弦定理得 ,
即 ,所以 ,
方程两边同除以 得 ,
解得 ,
又 ,故 ,
所以 满足要求, 舍去,
故 .故答案为:
15.(1)2
(2)
(1)求出 ,利用向量数量积运算法则得到 ,故 ,求出模长;
(2)利用向量夹角余弦公式得到 ,得到 .
【详解】(1) ,
故 ,
故 ,解得 ,
故 ,
所以 ;
(2) ,
又 ,故 .
16.(1)-1
(2)
(3)
(1)根据 得到 为实数,从而得到方程和不等式,求出答案;
(2)由 求出答案;
(3)根据第四象限的坐标特征得到不等式,求出答案.
【详解】(1) ,故 为实数,
,解得 ;(2)z为虚数,故 ,所以 ;
(3)由题意得 ,解得
17.(1) , ,理由见解析
(2)
(1)先得到伴随函数 ,由辅助角公式得到最大值 ;
(2)利用三角恒等变换得到 ,得到伴随向量 ,利用模长公式得到答案.
【详解】(1)向量 的伴随函数为 ,
,当 ,
即 时, 取得最大值,最大值 ;
(2)
,
故伴随向量 ,故 .
18.(1)证明过程见解析
(2)
(1)由正弦定理得到方程,计算出 ;
(2)作出辅助线,得到三角形全等, ,由余弦定理得到方程,求出 ,进而求出答案.
【详解】(1)由正弦定理得 ,
所以 ,即 ,又 ,故 ,所以 ;
(2)由(1)知, ,故 ,
延长 至点 ,使得 ,连接 ,
因为D为BC的中点,所以 ,
又 ,所以 ≌ ,
所以 ,
在 中, ,
由余弦定理得 ,
即 ,解得 ,
所以 .
19.(1)
(2)证明见解析
(3)存在,
【详解】(1)由正弦定理可得 ,即 ,即 ,
又 ,即 ,由余弦定理可得 .
(2)因为 ,所以 ,
即 .
则 .
故 ,
即 .
故 .
(3)存在 .下面给出证明.
因为 ,所以, .
展开整理可得 ,
即 ,
故 .
因此, .
所以,存在函数 .