文档内容
2024-2025 学年江苏省连云港市赣榆高级中学等校高一下学期 3 月学情
检测数学试卷
一、单选题:本题共8小题,每小题5分,共40分。在每小题给出的选项中,只有一项是符合题目要求的。
1.sin60∘cos30∘−cos120∘sin30∘=( )
√3−1 1 √3+1
A. B. C. D. 1
4 2 4
2.已知两个向量⃗ a=(1,2) ,⃗ b=(−x,1) ,若 ⃗a//⃗b ,则 x 的值为( )
1 1 √3 √3
A. − B. C. D. −
2 2 2 2
3.已知单位向量⃗a,⃗b的夹角为60°,则在下列向量中,与⃗b垂直的是( )
A. ⃗a+2⃗b B. 2⃗a+⃗b C. ⃗a−2⃗b D. 2⃗a−⃗b
4.在△ABC中,“AB2+BC2
|⃗
b
|,则 ⃗a>⃗b
C. 两个非零向量⃗
a,
⃗
b
,若|⃗
a+
⃗
b
|
=
|⃗
a−
⃗
b
|,则 ⃗a⊥⃗b
D. 若⃗a⋅⃗c=⃗b⋅⃗c,则⃗a=⃗b
10.已知 ( π) 5 3,则( )
α,β∈ 0, ,cos(α+β)= ,sin(α−β)=
2 13 5
12 4
A. sin(α+β)= B. cos(α−β)=−
13 5
63 tanα 7
C. sin2α= D. =
65 tanβ 33
1
11.正方形ABCD的边长为2,E在BC上,且BE= BC,如图,点P是以AB为直径的半圆上任意一点,
3
⃗ ⃗ ⃗
AP=λAD+μAE ,则( )
第 页,共 页
2 11
A. λ最大值为 B. μ最大值为1
3
C. ⃗ ⃗ 最大值是2√10 +2 D. | A ⃗ P+ 1 A ⃗ D |的最大值为 3+2√2
AP⋅AE
3 2
三、填空题:本题共3小题,每小题5分,共15分。
12.已知平面内两向量⃗
a=(3,5),
⃗
b=(cosθ,sinθ)
,若
⃗a⊥⃗b
,则
tanθ
的值为 .
13.已知 ,且 ( π) 3,则 ( π )的值为 .
α∈(0,π) sin α− +√3cosα= cos 2α−
3 5 12
14.如图,在▵ABC中,AB=2,AC=1,D,E分别是直线AC,AB上的点, A ⃗ E=2B ⃗ E,C ⃗ D=5A ⃗ C ,且
B ⃗ D⋅C ⃗ E=−1 ,则∠BAC= .若P是线段DE上的一个动点,则 B ⃗ P⋅C ⃗ P 的取值范围是 .
四、解答题:本题共5小题,共77分。解答应写出文字说明,证明过程或演算步骤。
15.(本小题13分)
⃗ ⃗ ⃗ ⃗ ⃗ ⃗ ⃗ ⃗ π
已知 m=2e +e ,n=λe −e ,其中 e ,e 是夹角为 的单位向量.
1 2 1 2 1 2 3
(1)当λ=3,求⃗m与⃗n夹角的余弦值;
(2)若⃗m与⃗n夹角为钝角,求λ的取值范围.
16.(本小题15分)
1 √2
已知α,β为锐角,tanα= ,cos(α+β)=− .
2 10
(1)求cos2α的值;
(2)求α−β的值.
17.(本小题15分)
第 页,共 页
3 1如图,A、B是单位圆上的相异两定点(O为圆心),且∠AOB=θ(θ为锐角).点C为单位圆上的动点,线段
AC交线段OB于点M.
求 ⃗ ⃗ 结果用 表示 ;
(1) OA⋅AB( θ )
若 ,求 ⃗ ⃗ 的取值范围.
(2) θ=60 ∘
CA⋅CB
18.(本小题17分)
设函数 f (x)=cosxcos ( x− π) +√3sin2x .
6
当 [ π π]时,求函数 的最小值并求出对应的 ;
(1) x∈ , f (x) x
12 2
在 中,角 的对边分别为 ,若 ,且 (A π) ,求 周长的取值范
(2) ▵ABC A,B,C a,b,c a=√3 f + =√3 ▵ABC
2 3
围.
19.(本小题17分)
设 O 为坐标原点,定义非零向量 O ⃗ M=(a,b) 的“相伴函数”为 f (x)=asinx+bcosx(x∈R) ,向量
O ⃗ M=(a,b) 称为函数 f (x)=asinx+bcosx 的“相伴向量”.
设函数 (π ) (π ),求 的“相伴向量”;
(1) ℎ(x)=2sin −x −cos +x ℎ(x)
3 6
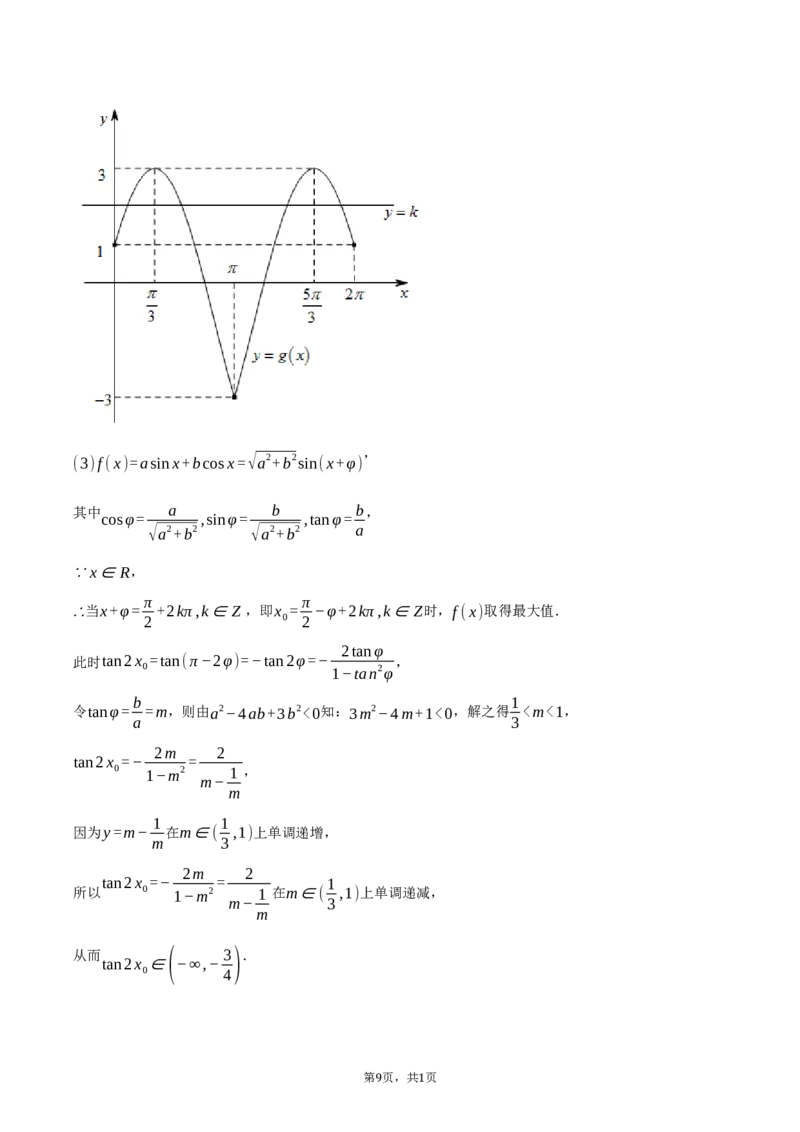
(2) 记 O ⃗ M=(0,2) 的“相伴函数”为 f (x) ,若函数 g(x)=f (x)+2√3|sinx|−1 , x∈[0,2π] 与直线 y=k 有
且仅有四个不同的交点,求实数k的取值范围;
(3)已知点M(a,b)满足3a2−4ab+b2<0,向量⃗OM的“相伴函数”f (x)在x=x 处取得最大值.当点M运
0
动时,求tan2x 的取值范围.
0
第 页,共 页
4 1参考答案
1.D
2.A
3.D
4.A
5.A
6.C
7.D
8.B
9.ABD
10.AC
11.BC
3
12.− /−0.6
5
31√2
13.−
50
π
14. ; ; ; ; ;
3
[171 ]
; ,25
28
⃗ ⃗ ⃗ ⃗ ⃗ π
15.【详解】(1)由已知,
m=2e +e
,
e ,e
是夹角为 的单位向量,
1 2 1 2 3
所以|⃗| √⃗ √( ⃗ ⃗) 2 √ ⃗ ⃗ ⃗ ⃗ √ π ,
m = m2= 2e +e = 4e 2+4e ⋅e +e 2= 4+4cos +1=√7
1 2 1 1 2 2 3
又 λ=3 ,则⃗
n=3e
⃗
−e
⃗,
1 2
所以|⃗| √⃗ √( ⃗ ⃗) √ ⃗ ⃗ ⃗ ⃗ √ π ,
n = n2= 3e −e = 9e 2−6e ⋅e +e 2= 9−6cos +1=√7
1 2 1 1 2 2 3
⃗ ⃗ ( ⃗ ⃗) ( ⃗ ⃗) ⃗ ⃗ ⃗ ⃗ π 1 11
又m⋅n= 2e +e ⋅ 3e −e =6e 2+e ⋅e −e 2=6+cos −1=6+ −1= ,
1 2 1 2 1 1 2 2 3 2 2
第 页,共 页
5 111
⃗ ⃗
所以 ⟨⃗ ⃗⟩ m⋅n 2 11.
cos m,n = = =
|⃗| |⃗| √7⋅√7 14
m⋅n
若 与 的夹角为钝角,则⃗ ⃗ 且⃗ ⃗不共线,
(2) ⃗m ⃗n
m⋅n<0 m,n
所以⃗ ⃗ ⃗ ⃗ ⃗ ⃗ ,且 ,
m⋅n=2λe 2+(λ−2)e ⋅e −e 2<0 λ≠−2
1 1 2 2
π 4
2λ+(λ−2)cos −1<0,且λ≠−2,所以λ< 且λ≠−2.
3 5
1 1 2
16.解:(1)因为α为锐角,且tanα= ,所以sinα= ,cosα= ,
2 √5 √5
2 3
所以cos2α=2cos2α−1=2×(
)
2−1=
.
√5 5
1 2 4
(2)由(1)知,sin2α=2sinαcosα=2× × = ,
√5 √5 5
√2 7√2
因为α,β为锐角,cos(α+β)=− ,所以sin(α+β)=√1−cos2 (α+β)= ,
10 10
4
则tan2α= ,tan(α+β)=−7,
3
则 tan2α−tan(α+β) ,
tan(α−β)=tan[2α−(α+β)]= =−1
1+tan2αtan(α+β)
π π
因为α,β为锐角,所以− <α−β< ,
2 2
π
所以α−β=− .
4
⃗ ⃗ ⃗ ( ⃗ ⃗ ) ⃗ ⃗ θ
17.【详解】(1)OA⋅AB=OA⋅OB−OA =OA⋅OB−1=cosθ−1=−2sin2 ;
2
⃗ ⃗ 1
(2)当θ=60 ∘时,OA⋅OB= ,
2
⃗ ⃗ ( ⃗ ⃗ ) ( ⃗ ⃗ ) ⃗ ⃗ ⃗ ⃗ ⃗ ⃗ .
CA⋅CB= OA−OC ⋅OB−OC =OA⋅OB−OA⋅OC−OC⋅OB+1
第 页,共 页
6 1设 ,由条件知: [ 2π],
∠BOC=α α∈ 0,
3
⃗ ⃗ 3 (π ) 3 1 √3 3 3 √3
∴CA⋅CB= −cos +α −cosα= − cosα+ sinα−cosα= − cosα+ sinα
2 3 2 2 2 2 2 2
3 (√3 1 ) 3 ( π),
= −√3 cosα− sinα = −√3cos α+
2 2 2 2 6
[ 2π],则 π [π 5π],
∵α∈ 0, α+ ∈ ,
3 6 6 6
( π) [ √3 √3], ⃗ ⃗ .
∴cos α+ ∈ − ,
∴CA⋅CB∈[0,3]
6 2 2
18.【详解】(1)因为
f (x)=cosxcos ( x− π) +√3sin2x= √3 cosxcosx+ 1 cosxsinx+√3sin2x
6 2 2
√3 1 √3 √3 1
= cos2x+ sin2x+√3sin2x= sin2x+ + sin2x
2 4 2 2 4
1 √3 3√3 1 ( π) 3√3,
= sin2x− cos2x+ = sin 2x− +
4 4 4 2 3 4
因为 [ π π],所以 π [ π 2π],
x∈ , 2x− ∈ − ,
12 2 3 6 3
π π π 1 3√3
由y=sinx的图象与性质知,当2x− =− ,即x= 时,函数f (x)取到最小值为− + ,
3 6 12 4 4
即当 [ π π]时,函数 的最小值为 1 3√3,此时 π .
x∈ , f (x) − + x=
12 2 4 4 12
因为 (A π) ,由 得到,
(2) f + =√3 (1)
2 3
1 [ (A π) π] 3√3 1 ( π) 3√3 ,
sin 2× + − + = sin A+ + =√3
2 2 3 3 4 2 3 4
第 页,共 页
7 1即 ( π) √3,又在 中 ,则 π (π 4π),
sin A+ = ▵ABC A∈(0,π) A+ ∈ ,
3 2 3 3 3
π 2π π
所以A+ = ,即A= ,
3 3 3
又a=√3,由余弦定理a2=b2+c2−2bccosA,得到3=b2+c2−bc,
又由基本不等式知, (b+c) 2,当且仅当 取等号,
bc≤ b=c
2
1
所以3=b2+c2−bc=(b+c) 2−3bc≥ (b+c) 2,则b+c≤2√3,
4
又因为b+c>a=√3,所以2√3