文档内容
2024-2025 学年江西省三新协同教研共同体高一下学期 5 月联考
数学试卷
一、单选题:本题共8小题,每小题5分,共40分。在每小题给出的选项中,只有一项是符合题目要求的。
z
1.已知复数z满足 =2−i,其中i为虚数单位,则z在复平面内对应的点位于( )
1+i
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
2.已知向量⃗
a=(2,−m)
,⃗
b=(3m+2,2)
,且 ⃗a⊥⃗b ,则
3
⃗
a+
⃗
b=
( )
A. (2,1) B. (5,5) C. (−1,2) D. (6,3)
3.已知角α的终边过点(3,−4),则sin2α=( )
3 3 24 24
A. B. − C. − D.
5 5 25 25
⃗ 1 ⃗ ⃗ ⃗ 2 ⃗
4.在△ABC中,AN= NC,P是直线BN上的一点,若AP=mAB+ AC,则实数m的值为( )
3 5
3 3 1 1
A. − B. C. D. −
5 5 5 5
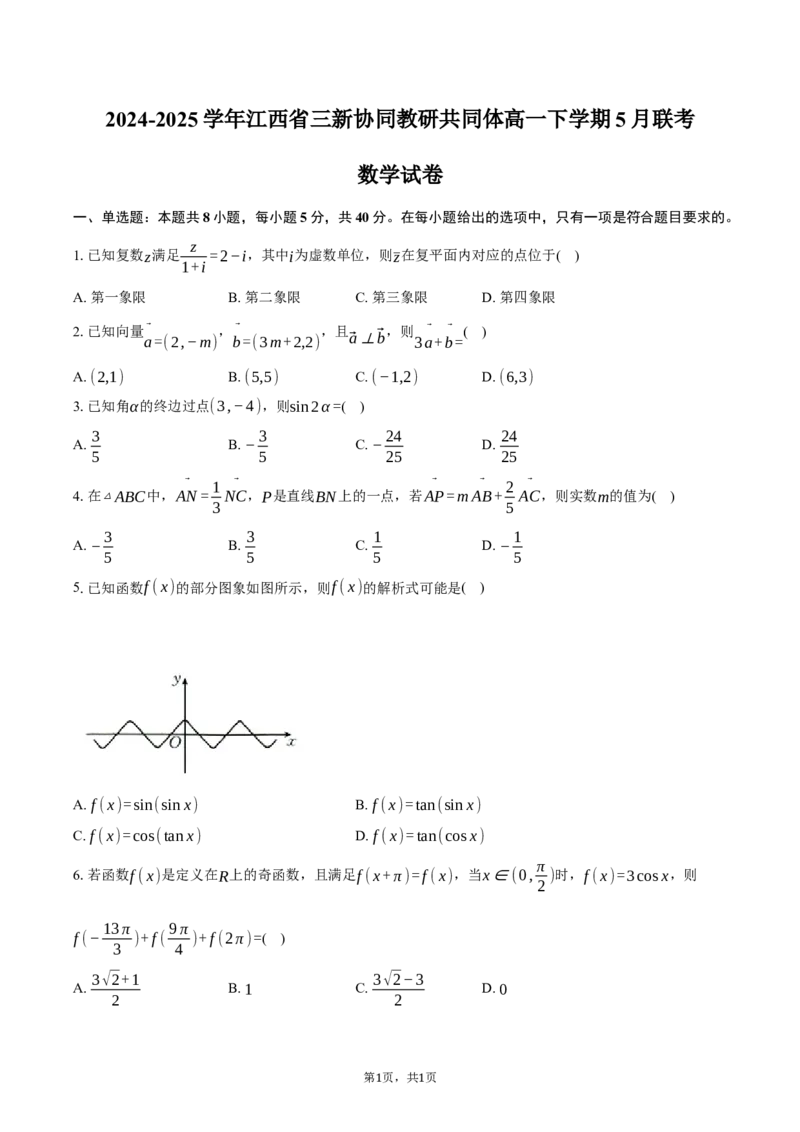
5.已知函数f(x)的部分图象如图所示,则f(x)的解析式可能是( )
A. f(x)=sin(sinx) B. f(x)=tan(sinx)
C. f(x)=cos(tanx) D. f(x)=tan(cosx)
π
6.若函数f(x)是定义在R上的奇函数,且满足f(x+π)=f(x),当x∈(0, )时,f(x)=3cosx,则
2
13π 9π
f(− )+f( )+f(2π)=( )
3 4
3√2+1 3√2−3
A. B. 1 C. D. 0
2 2
第 页,共 页
1 1πx
7.方程x2−2x⋅cos +1=0的实数解的个数为( )
2
A. 0 B. 1 C. 2 D. 3
π π
8.设A,B,C是函数f(x)=sin( −ωx)(ω>0)与函数g(x)=cos(ωx− )(ω>0)的图象连续相邻的三
2 3
个交点,若△ABC是锐角三角形,则ω的取值范围是( )
√3π √2π √2π √3π
A. ( ,+∞) B. ( ,+∞) C. (0, ) D. (0, )
3 2 2 3
二、多选题:本题共3小题,共18分。在每小题给出的选项中,有多项符合题目要求。
π
9.已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|< )的部分图象如图所示,则( )
2
π
A. f( )=−√3
2
π π
B. 将f(x)的图象向右平移 个单位长度,得到y=2sin(2x− )的图象
3 3
5π
C. 直线x= 为f(x)图象的一条对称轴
6
π
D. 直线y=√3与f(x)的图象相交,存在两个交点的横坐标t ,t ,使得|t −t |=
1 2 1 2 6
10.任何一个复数z都可以表示为reiθ,且可以表示为三角形式r(cosθ+isinθ),r代表复数z的模,θ是以
x轴的非负半轴为始边,以OZ所在的射线为终边的角.著名数学家棣莫弗就此进行了深度探究,发现
,该公式称为棣莫弗公式 根据上面的知识,若复数
[r(cosθ+isinθ)] n=rn (cosnθ+isinnθ)(n∈N∗) . z
满足z7=128,则z可能的取值为( )
第 页,共 页
2 13π 3π 2π 2π
A. 2(cos +isin ) B. 2(cos +isin )
7 7 7 7
π π 6π 6π
C. 2(cos +isin ) D. 2(cos +isin )
7 7 7 7
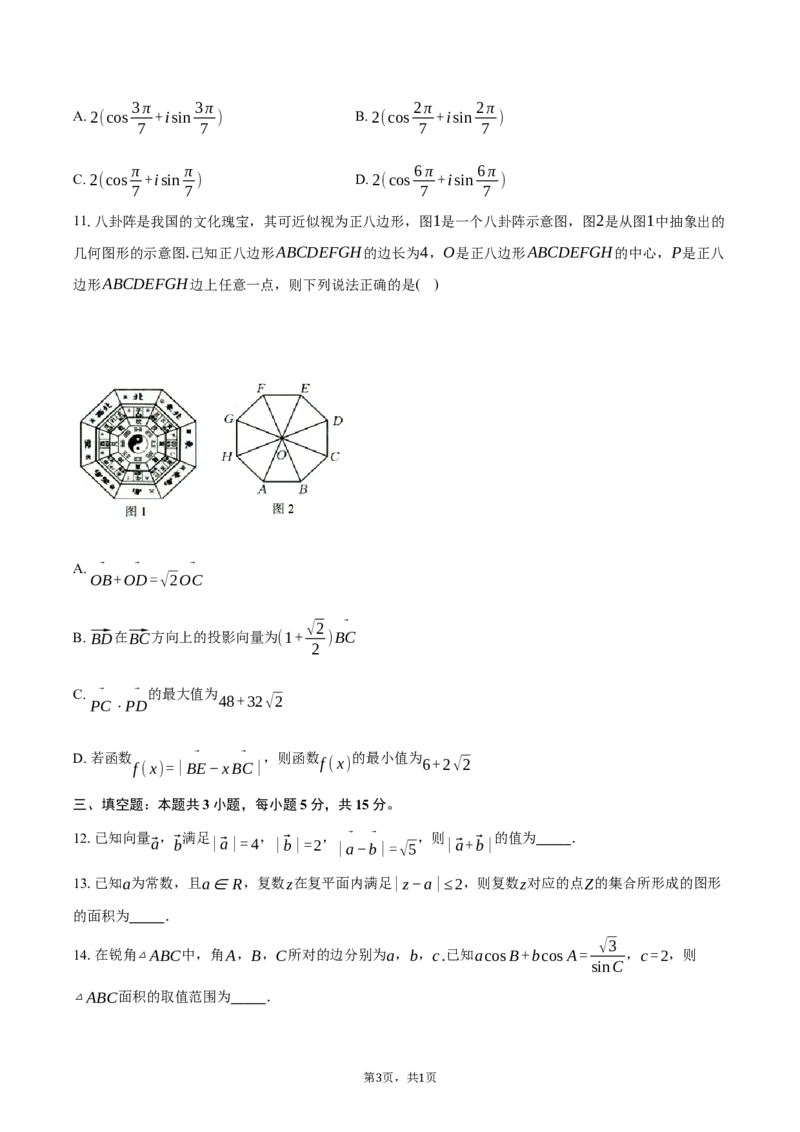
11.八卦阵是我国的文化瑰宝,其可近似视为正八边形,图1是一个八卦阵示意图,图2是从图1中抽象出的
几何图形的示意图.已知正八边形ABCDEFGH的边长为4,O是正八边形ABCDEFGH的中心,P是正八
边形ABCDEFGH边上任意一点,则下列说法正确的是( )
A. ⃗ ⃗ ⃗
OB+OD=√2OC
√2 ⃗
B. ⃗BD在⃗BC方向上的投影向量为(1+ )BC
2
C. ⃗ ⃗ 的最大值为
48+32√2
PC⋅PD
D. 若函数 f(x)=|B ⃗ E−xB ⃗ C| ,则函数 f(x) 的最小值为 6+2√2
三、填空题:本题共3小题,每小题5分,共15分。
12.已知向量 ⃗a , ⃗b 满足 |⃗a|=4 , |⃗b|=2 ,
|
⃗
a−
⃗
b|=√5
,则 |⃗a+⃗b| 的值为 .
13.已知a为常数,且a∈R,复数z在复平面内满足|z−a|≤2,则复数z对应的点Z的集合所形成的图形
的面积为 .
√3
14.在锐角△ABC中,角A,B,C所对的边分别为a,b,c.已知acosB+bcosA= ,c=2,则
sinC
△ABC面积的取值范围为 .
第 页,共 页
3 1四、解答题:本题共5小题,共77分。解答应写出文字说明,证明过程或演算步骤。
15.(本小题13分)
已知复数z满足|z|=√2,z2的虚部为−2.
(1)求z;
(2)若z的实部为正数,z,z2,2z+z2在复平面内对应的点分别为A,B,C,求cos∠BAC.
16.(本小题15分)
π x x π
2sin(−x)sin( − )cos( − )
4 2 2 4
已知函数f(x)= .
x x x x
(cos +sin )(sin −cos )
2 2 2 2
(1)化简f(x);
4√3 11
(2)已知α,β都是锐角,sinα= ,cos(α+β)=− ,求f(β)的值.
7 14
17.(本小题15分)
在△ABC中,角A,B,C的对边分别为a,b,c.
π √3
(1)若∠ACB= ,∠ACB的平分线交AB于点D,且a+b= ab,求CD的值;
3 4
若角 , , 满足 ,且 ,证明:该三角形
(2) A B C sin2A+sin2B+sin2C=2(cos2A+cos2B+cos2C) a>b>c
是直角三角形.
18.(本小题17分)
设函数 .
f(x)=sin2x−2acosx+a+1(a∈R)
(1)求f(x)在R上的最大值;
π
(2)若不等式f(x)>0在[0, ]上恒成立,求a的取值范围;
3
(3)若方程f(x)=1−2acosx在(0,2π]上有4个不相等的实数根,求a的取值范围.
19.(本小题17分)
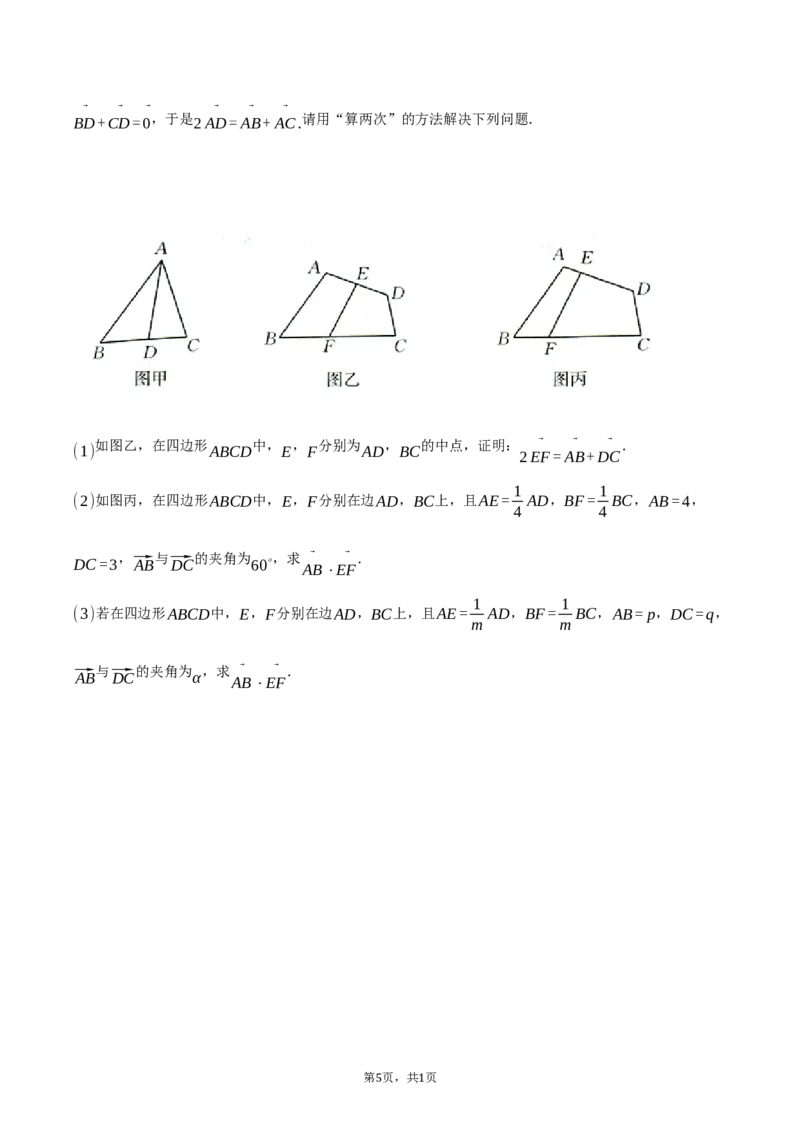
“算两次”原理(又称富比尼原理)是一种重要的数学思想,其核心是通过对同一量采用两种不同的计算方
式,利用结果的等价性构建等式来解决问题.例如:如图甲,在△ABC中,D为BC的中点,则
⃗ ⃗ ⃗ ⃗ ⃗ ⃗ ⃗ ⃗ ⃗ ⃗ ⃗
AD=AB+BD , AD=AC+CD ,两式相加得 2AD=AB+BD+AC+CD ,因为D为BC的中点,所以
第 页,共 页
4 1⃗ ⃗ ⃗ ⃗ ⃗ ⃗
BD+CD=0 ,于是 2AD=AB+AC. 请用“算两次”的方法解决下列问题.
如图乙,在四边形 中, , 分别为 , 的中点,证明: ⃗ ⃗ ⃗ .
(1) ABCD E F AD BC
2EF=AB+DC
1 1
(2)如图丙,在四边形ABCD中,E,F分别在边AD,BC上,且AE= AD,BF= BC,AB=4,
4 4
DC=3 , ⃗AB 与 ⃗DC 的夹角为 60∘ ,求 ⃗ ⃗ .
AB⋅EF
1 1
(3)若在四边形ABCD中,E,F分别在边AD,BC上,且AE= AD,BF= BC,AB=p,DC=q,
m m
与 的夹角为 ,求 ⃗ ⃗ .
⃗AB ⃗DC α
AB⋅EF
第 页,共 页
5 1参考答案
1.D
2.B
3.C
4.A
5.D
6.C
7.A
8.A
9.ABD
10.BD
11.ABC
12.√35
13.4π
2√3
14.( ,√3]
3
15. 设 ,则 ,
(1) z=x+ yi(x,y∈R) z2=(x+ yi) 2=x2−y2+2xyi
则{x2+ y2=2,
2xy=−2,
{x=1, {x=−1,
解得 或
y=−1 y=1,
∴z=1−i或z=−1+i.
的实部为正数, , , ,
(2)∵z ∴z=1−i ∴z2=(1−i) 2=−2i 2z+z2=2−4i
则 , , ,则 ⃗ , ⃗ ,
A(1,−1) B(0,−2) C(2,−4)
AB=(−1,−1) AC=(1,−3)
⃗ ⃗
AB⋅AC 2 √5
∴cos∠BAC= = = .
⃗ ⃗ √2×√10 5
|AB||AC|
第 页,共 页
6 1π x x π 1 π
2sin(−x)sin( − )cos( − ) −2sinx⋅ sin( −x)
4 2 2 4 2 2
16.解:(1)f(x)= =
x x x x x x
(cos +sin )(sin −cos ) sin2 −cos2
2 2 2 2 2 2
−sinxcosx π
= =sinx(x≠ +kπ,k∈Z);
−cosx 2
4√3 1
(2)因为角α为锐角,且sinα= ,所以cosα=√1−sin2α= .
7 7
π π
因为α∈(0, ),β∈(0, ),所以α+β∈(0,π),
2 2
11 5√3
又因为cos(α+β)=− ,所以sin(α+β)=√1−cos2 (α+β)= ,
14 14
所以f(β)=sinβ=sin[(α+β)−α]=sin(α+β)cosα−cos(α+β)sinα
5√3 1 11 4√3 √3
= × −(− )× = .
14 7 14 7 2
π C π C 1
17.解:(1)因为C= ,所以 = ,所以sin = .
3 2 6 2 2
1 1 C 1 C
由S =S +S ,得 absinC= CD⋅asin + CD⋅bsin ,
△CAB △CAD △CBD 2 2 2 2 2
√3 1
所以 ab= CD⋅(a+b),
2 2
√3ab 4
所以CD= =√3× =4.
a+b √3
由于 ,
(2) sin2A+sin2B+sin2C=2(cos2A+cos2B+cos2C)
因此 ,
1−cos2A+1−cos2B+1−cos2C=2(cos2A+cos2B+cos2C)
所以 ,所以 ;
3(cos2A+cos2B+cos2C)=3 cos2A+cos2B+cos2C=1
则 ,
2(cos2A+cos2B+cos2C)=2
第 页,共 页
7 1所以cos2A+cos2B+2cos2C=0,
所以 ,即 ,
2cos(A+B)cos(A−B)+2cos2C=0 −2cosCcos(A−B)+2cos2C=0
即cosC[cosC−cos(A−B)]=0,
故cosC=0或cosC=cos(A−B).
由a>b>c,可得π>A>B>C>0,所以π>A−B>0,π>C>0,
π
所以C= 或A−B=C.
2
π
由A>B>C,可得C< ,故A=B+C,
2
因此该三角形为直角三角形.
18.解: ,
(1)f(x)=1−cos2x−2acosx+a+1=−cos2x−2acosx+a+2
令 ,得
t=cosx∈[−1,1] g(t)=−t2−2at+a+2
①当−a<−1,即a>1时,f(x) =g(−1)=3a+1.
max
当 ,即 时, .
② −1≤−a≤1 −1≤a≤1 f(x) =g(−a)=a2+a+2
max
③当−a>1,即a<−1时,f(x) =g(1)=−a+1.
max
{
3a+1,a>1,
综上可知,
f(x) = a2+a+2,−1≤a≤1,
max
−a+1,a<−1.
π 1
(2)若要f(x)>0,则需f(x) >0,当x∈[0, ]时,t=cosx∈[ ,1],
min 3 2
1
函数y=f(x)变为g(t)=−t2−2at+a+2,t∈[ ,1],所求问题变为g(t) >0恒成立.
2 min
易知g(t)的图象是开口向下的抛物线的一部分,最小值一定在区间端点处取得,
第 页,共 页
8 1{ 1
所以有 g( )>0,,解得 ,故 的取值范围是 .
2 a<1 a (−∞,1)
g(1)>0,
方法一 原方程 可化为 .
(3)( ) f(x)=−cos2x−2acosx+a+2=1−2acosx cos2x−a−1=0
令t=cosx∈[−1,1],即t2−a−1=0,a=t2−1.
当t∈(−1,1)时,t=cosx在x∈(0,2π]上一个t对应两个不相等的实数解,
因此原题可转化为y=a与y=t2−1的图象在t∈(−1,1)上有两个不同的交点,
即{a>02−1,
a<12−1,
故a的取值范围是(−1,0).
(方法二)原方程可以化为cos2x=2a+1,
可以看作y=cos2x与y=2a+1的图象在x∈(0,2π]上有四个不同的交点,
则−1<2a+1<1,
故a的取值范围是(−1,0).
19.解: 在四边形 中, ⃗ ⃗ ⃗ ⃗ ,
(1) ABFE EF=EA+AB+BF ①
在四边形 中, ⃗ ⃗ ⃗ ⃗ ,
CDEF EF=ED+DC+CF ②
由 ①+② ,得
2E
⃗
F=E
⃗
A+A
⃗
B+B
⃗
F+E
⃗
D+D
⃗
C+C
⃗
F
.
因为 , 分别为 , 的中点,所以 ⃗ ⃗ ⃗, ⃗ ⃗ ⃗,
E F AD BC
EA+ED=0 CF+BF=0
于是 ⃗ ⃗ ⃗ .
2EF=AB+DC
在四边形 中, ⃗ ⃗ ⃗ ⃗ ,
(2) ABFE EF=EA+AB+BF ③
在四边形 中, ⃗ ⃗ ⃗ ⃗ ,
CDEF EF=ED+DC+CF ④
第 页,共 页
9 1⃗ 1 ⃗ ⃗ 1 ⃗
由AE= AD,BF= BC,得 ⃗ ⃗ ⃗ , ⃗ ⃗ ⃗ ,
3EA+ED=0 BF+CF=0
4 4
③×3+④ ⃗ 3 ⃗ 1 ⃗
由 ,得EF= AB+ DC,
4 4 4
⃗ ⃗ ⃗ 3 ⃗ 1 ⃗ 3 ⃗ 1 ⃗ ⃗
所以AB⋅EF=AB⋅( AB+ DC)= AB2+ AB⋅DC
4 4 4 4
3 ⃗ 1 ⃗ ⃗ 3 1 1 27
= |AB|2+ |AB||DC|cos60∘= ×42+ ×4×3× = .
4 4 4 4 2 2
在四边形 中, ⃗ ⃗ ⃗ ⃗ ,
(3) ABFE EF=EA+AB+BF ⑤
在四边形 中, ⃗ ⃗ ⃗ ⃗ ,
CDEF EF=ED+DC+CF ⑥
⃗ 1 ⃗ ⃗ 1 ⃗ ⃗ ⃗ ⃗ ⃗ ⃗ ⃗
由AE= AD,BF= BC,得 (m−1)EA+ED=0 , (m−1)BF+CF=0 ,
m m
⑤×(m−1)+⑥ ⃗ m−1 ⃗ 1 ⃗
由 ,得EF= AB+ DC.
m m m
故 ⃗ ⃗ ⃗ m−1 ⃗ 1 ⃗ m−1 ⃗ 1 ⃗ ⃗
AB⋅EF=AB⋅( AB+ DC)= AB2+ AB⋅DC
m m m m
m−1 ⃗ 1 ⃗ ⃗ m−1 1
= |AB|2+ |AB||DC|cosα= ×p2+ ×p×q×cosα
m m m m
p
= (pm−p+qcosα).
m
第 页,共 页
10 1