文档内容
江西省赣州市 2024-2025 学年高一上学期 1 月期末数学试题
第I卷(选择题)
一、单选题:本题共8小题,每小题5分,共40分。在每小题给出的选项中,只有一项是符合题目要求的。
1.若集合 , ,则 ( )
A={x|x=2n,n∈N} B={x|x2-5x-6≤0} A∩B=
A. {2,4} B. {0,2,4} C. {2,4,6} D. {0,2,4,6}
2.为深入学习宣传党的二十大精神,某校开展了“奋进新征程,强国伴我行”二十大主题知识竞赛.其中高
一年级选派了10名同学参赛,且该10名同学的成绩依次是71,73,80,85,90,92,94,95,98,
100,则60%分位数为( )
A. 92 B. 93 C. 94 D. 87.8
1 1
3.已知事件A,B相互独立,且P(A)= ,P(B)= ,则P(AB)=( )
3 4
1 1 1 2
A. B. C. D.
6 12 3 3
m
4.若函数f(x)=1- 为奇函数,则( )
2x+1
A. m=2 B. m=1 C. m=-1 D. m=0
5.命题“m∈(2,+∞)”为真命题的充分不必要条件是( )
A. m≥2 B. m≥3 C. m>2 D. m≥1
6.某科研小组培育一种水稻新品种,由第1代1粒种子可以得到第2代120粒种子,以后各代每粒种子都可
以得到下一代 粒种子,则第 代得到的种子数为( ) 参考数据: ,
120 10 ( 1.29≈5.16 1.210≈6.19)
A. 5.16×109 B. 6.19×1010 C. 5.16×1018 D. 6.19×1020
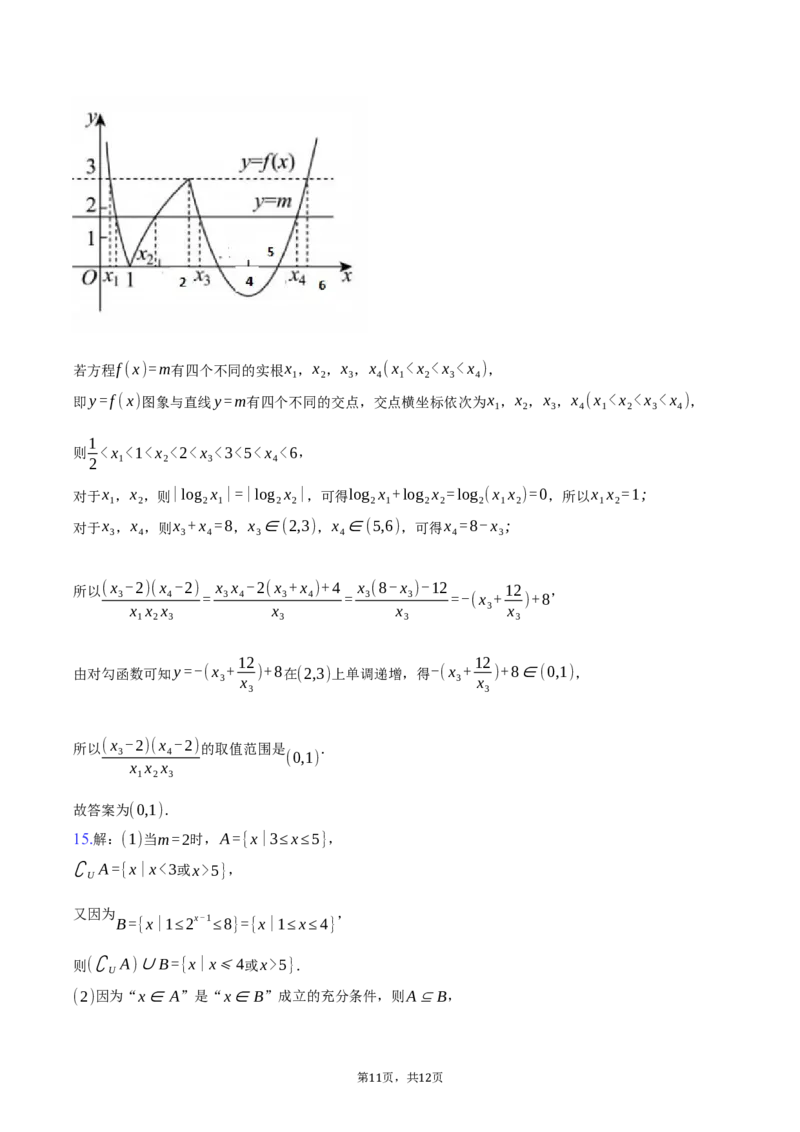
7.函数 ,且 ,则 和 的不等关系正确的是( )
f(x)=x2-2x+2 a>b>1 f(ax ) f(bx )
A. B. C. D.
f(ax )>f(bx
)
f(ax )0对任意x∈R恒成立,则实数a的取值范围是02 1 2 3
x (x b>1,
∴若x⩾0,则ax ⩾bx ⩾1,此时ax-bx ⩾0,ax+bx-2⩾0,
则 ,即 ;
(ax-bx )(ax+bx-2)⩾0 f(ax )⩾f(bx
)
若x<0,则ax0 f(ax )>f(bx ).
综上, ,
f(ax )⩾f(bx
)
故选C.
8.【答案】A
第 页,共 页
6 12【解析】由于函数 在区间 上有且仅有一个不动点和一个次不动点,
g(x)=log (4x-m⋅2x ) [0,1]
2
所以 以及 ,都有且仅有 个根,
log (4x-m⋅2x )=x log (4x-m⋅2x )=-x 1
2 2
由 ,即 ,即 在 有且仅有 个根,
(1) log (4x-m⋅2x )=x 4x-m⋅2x=2x m=2x-1 [0,1] 1
2
即20-1⩽m⩽21-1,即0⩽m⩽1,
1
(2)由log (4x-m⋅2x )=-x,即4x-m⋅2x=2-x,即m=2x- 在[0,1]有且仅有1个根,
2 4x
1
易得函数y=2x-
在[0,1]上单调递增,
4x
1 1 7
则20- ⩽m⩽21-
,即0⩽m⩽ ,
40 41 4
综合(1)、(2)可知,0⩽m⩽1,
故选A.
9.【答案】AC
1 1
【解析】对于A,命题“∀x∈(1,+∞),都有 <1”的否定为“∃x ∈(1,+∞),使得 ≥1”故A正
x 0 x
0
确;
对于 ,函数 是由函数 和 复合而成,
B f(x)=log (-x2+2x+3) y=log u u=-x2+2x+3
3 3
由于函数y=log u单调递增,解-x2+2x+3>0,得-10对任意x∈R恒成立,当a=0时,1>0恒成立,故a的值可以为0,故D错
第 页,共 页
7 12误,
故选AC.
10.【答案】ABC
【解析】A选项,易得函数f(x)的定义域为{x|x≠±1},
1+(-x) 2 ,故 为偶函数,故A选项正确.
f(-x)= =f(x) f(x)
1-(-x) 2
1
1+( ) 2
1 x x2+1 1+x2 x2+1
B选项,f( )= = ,-f(x)=- = ,
x
1-(
1
) 2
x2-1 1-x2 x2-1
x
1
所以f( )=-f(x)(x≠0),故B选项正确;
x
选项,因为 1+x2 -(1-x2 )+2 2 ,
C f(x)= = =-1+
1-x2 1-x2 1-x2
设 ,因为 在 上单调递减,所以 1+x2在 单调递增,故C选项正
y=1- x2 y=1- x2 (1,+ ∞) f(x)= (1,+ ∞)
1-x2
确;
2
D选项,由C选项知f(x)=-1+ ,
1-x2
2 2
因为1- x2 ⩽1,则 ∈(-∞,0)∪[2,+∞), -1+ ∈(-∞,-1)∪[1,+∞),
1-x2 1-x2
函数f(x)的值域为 (-∞,-1)∪[1,+∞),故D错误.
故选ABC.
11.【答案】AD
【解析】因为 2m+n=1,
1
又因为 2m+n⩾2√2mn,即 mn⩽ ,
8
第 页,共 页
8 121
当且仅当n=2m= 时等号成立,
2
1
log m+log n=log mn⩽log =-3,故log m+log n的最大值为-3,
2 2 2 28 2 2
故A正确;
1 1 1 1 n 2m
因为 + =(2m+n)( + )=3+ + ⩾3+2√2,
m n m n m n
当且仅当 n=√2m且 2m+n=1,
√2
即 m=1- ,n=√2-1时等号成立,故B错误;
2
因为2m+n=1,所以2(m+1)+n+2=5
2 9 1 2 9
+ = ( + )[2(m+1)+n+2]
m+1 n+2 5 m+1 n+2
1 2(n+2) 18(m+1) 1
= (13+ + )⩾ ×(13+12)=5,
5 m+1 n+2 5
当且仅当 n=3m+1且 2m+n=1,
即m=0,n=1时,等号成立,
又实数 m>0,n>0,所以等号不成立,故C错误;
因为 m2+n2=m2+(1-2m) 2=5m2-4m+1=5 ( m- 2) 2 + 1,
5 5
2 1 1
当m= ,n= 时,m2+n2的最小值为 ,故D正确.
5 5 5
故选AD.
12.【答案】4
【解析】因为 ,
f(x)=4x+log x
2
所以 1 1 1 .
f( )=42+log =2-1=1
2 22
第 页,共 页
9 121
则f(f( ))=f(1)=4-0=4,
2
故答案为4.
13.【答案】(-1,3)
【解析】∵函数f(2x-1)的定义域为(0,2),
∴02
当 时, ,可知其对称轴为 ,
x>2 f(x)=x2-8x+15=(x-4) 2-1 x=4
令x2-8x+15=0,解得x=3或x=5;
令x2-8x+15=3,解得x=2或x=6;
1
当05},
U
又因为 ,
B={x|1≤2x-1≤8}={x|1≤x≤4}
则(∁ A)∪B={x|x⩽4或x>5}.
U
(2)因为“x∈A”是“x∈B”成立的充分条件,则A⊆B,
第 页,共 页
11 12集合A={x|m+1≤x≤3m-1},B={x|1≤x≤4},
当A=⌀时,m+1>3m-1,即m<1.符合题意;
{m+1⩽3m-1
5
当A≠⌀时, m+1⩾1 ,解得:1⩽m⩽ .
3
3m-1⩽4
5
综上所述,实数m的取值范围是{m|m⩽ }.
3
16.解:(1)函数f(x)为幂函数,则2a2-3a+2=1,
即(2a-1)(a-1)=0,
1
因为a≠1,所以a= ,
2
1
得
f(x)=x2
,则函数f(x) 在 [0,+∞) 上单调递增,
下面证明:
任取x ,x ∈[0,+∞),且x 0
1 2 1 2 1 2
得 ,即 ,
f(x )-f (x )<0 f(x )1时,m⩽ ,
t-1
t2-2t+5 4 √ 4
而 =t-1+ ⩾2 (t-1)· =4,
t-1 t-1 t-1
当且仅当t=3时等号成立,
则m⩽4,
故实数m的取值范围为:(-∞,4]
17.解:(1)对于Q(v)=1000log v+b ,当v=0 时,它无意义,所以不符合题意;
a
8
对于Q(v)=100⋅( ) v+a ,它显然是个减函数,所以不符合题意,
9
1
故选Q(v)= v3+bv2+cv .
50
1
{ ×103+b×102+c×10=1320
根据提供的数据,则有 50 ,解得 ,
b=-2,c=150
1
×303+b×302+c×30=3240
50
1
当0⩽v<80 时,Q(v)= v3-2v2+150v .
50
100
(2)设车速为vkm/h ,行驶时百公里所用时间为 h ,
v
100 1
所耗电量M(v)= ( v3-2v2+150v)
v 50
,
=2(v2-100v+7500)=2(v-50) 2+10000
要使耗电量达到最小,则v=50 .
最小耗电量为10000W h .
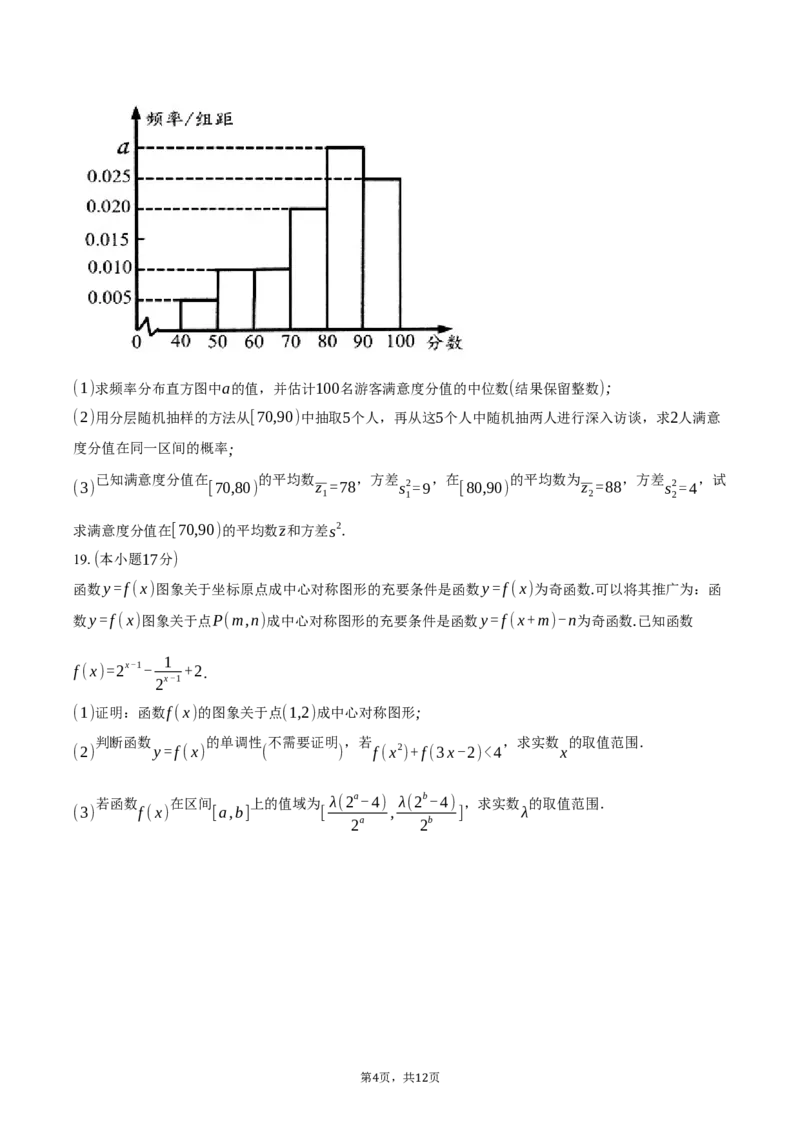
18.解:(1)由(0.005+0.010×2+0.020+a+0.025)×10=1,解得a=0.030;
满意度分值在[40,80)的频率为(0.005+0.010×2+0.020)×10=0.45<0.5,
在[40,90)的频率为(0.005+0.010×2+0.020+0.030)×10=0.75>0.5,
所以中位数落在区间[80,90)内,
第 页,共 页
13 120.5-0.45 245
所以中位数为80+10× = ≈82;
0.3 3
(2)从[70,80)中抽取2人,记为A,B,
从[80,90)中抽取3人,记为a,b,c
所以5个人中随机抽取两人,抽取的结果有:
{(ab),(ac),(aA),(aB),(bc),(bA),(bB),(cA),(cB),(AB)},共有10种情况,
4 2
取到2人满意度分值在同一区间有{(ab),(ac),(bc),(AB)}有4种情况,所以概率为 = ,
10 5
2
∴2人满意度分值在同一区间的概率为 ;
5
(3)满意度分值在[70,80)的频率为0.02×10=0.2,人数为20;
在[80,90)的频率为0.03×10=0.3,人数为30,
满意度分值在 的平均数 ,方差 ,
[70,80) z =78 s2=9
1 1
在 的平均数 ,方差 ,
[80,90) z =88 s2=4
2 2
20z +30z
所以满意度分值在[70,90)的平均数z= 1 2=84,
50
20 30
满意度分值在[70,90)的方差为s2= [s2+(z -z) 2 ]+ [s2+(z -z) 2 ]
50 1 1 50 2 2
=30.
19. (1)证明:由题意得:函数f(x)的定义域为R,
又 ,令 ,可知: ,
y=f(x+1)-2=2x-2-x g(x)=f(x+1)-2=2x-2-x g(-x)=2-x-2x
从而g(-x)=-g(x),所以g(x)是奇函数,即y=f(x+1)-2是奇函数,
故函数f(x)图象关于点(1,2)成中心对称图形.
解: 在 上是增函数,
(2) g(x)=2x-2-x (-∞,+∞)
1
所以函数f(x)=2x-1- +2在(-∞,+∞)上也是增函数,
2x-1
第 页,共 页
14 12由 可得 ,即 ,
f(x2 )+f(3x-2)<4 f(x2-1+1)-2+f(3x-3+1)-2<0 g(x2-1)+g(3x-3)<0
所以 ,又函数 在 上是增函数,
g(x2-1)0
所以 ,解得 ,
8λ-4>0 λ>6+2√7
2-λ<0
所以实数λ的取值范围是(6+2√7,+∞).
第 页,共 页
15 12