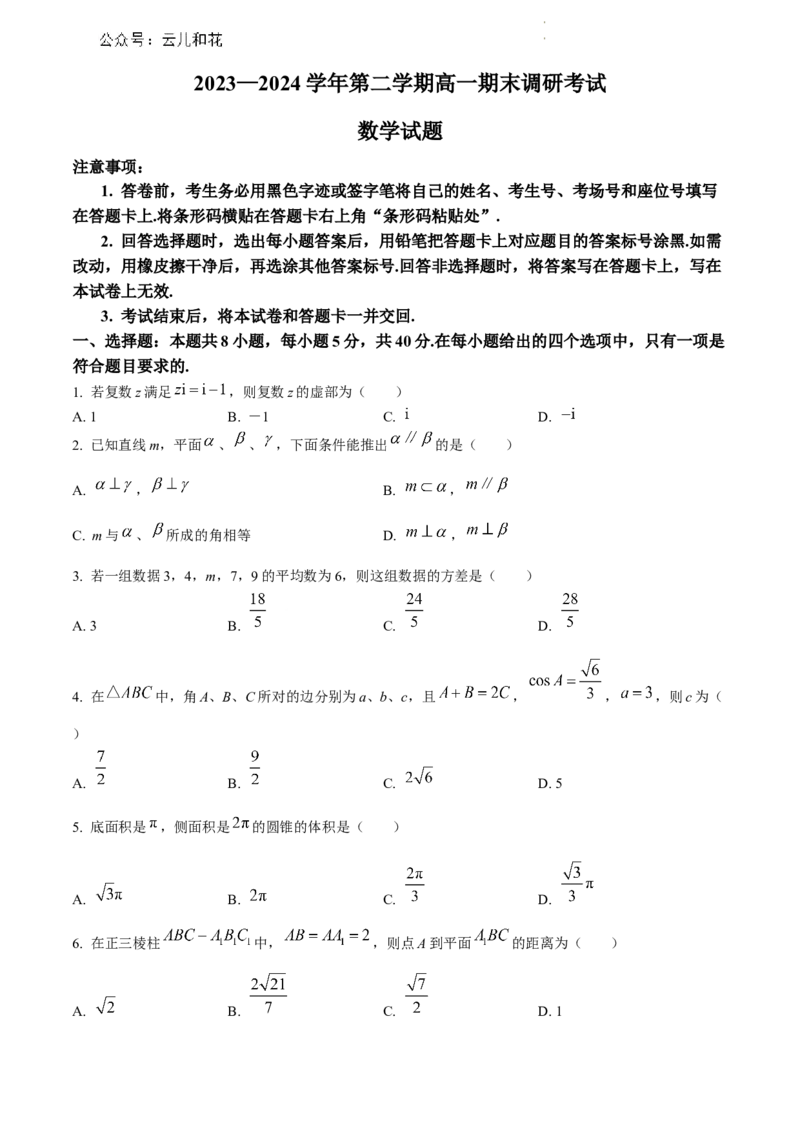文档内容
2023—2024 学年第二学期高一期末调研考试
数学试题
注意事项:
1. 答卷前,考生务必用黑色字迹或签字笔将自己的姓名、考生号、考场号和座位号填写
在答题卡上.将条形码横贴在答题卡右上角“条形码粘贴处”.
2. 回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑.如需
改动,用橡皮擦干净后,再选涂其他答案标号.回答非选择题时,将答案写在答题卡上,写在
本试卷上无效.
3. 考试结束后,将本试卷和答题卡一并交回.
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是
符合题目要求的.
1. 若复数z满足 ,则复数z的虚部为( )
A. 1 B. -1 C. D.
2. 已知直线m,平面 、 、 ,下面条件能推出 的是( )
A. , B. ,
C. m与 、 所成的角相等 D. ,
3. 若一组数据3,4,m,7,9的平均数为6,则这组数据的方差是( )
A. 3 B. C. D.
4. 在 中,角A、B、C所对的边分别为a、b、c,且 , , ,则c为(
)
A. B. C. D. 5
5. 底面积是 ,侧面积是 的圆锥的体积是( )
A. B. C. D.
6. 在正三棱柱 中, ,则点A到平面 的距离为( )
A. B. C. D. 1
学学科科网网((北北京京))股股份份有有限限公公司司7. 一个盒子里装有除颜色外完全相同的四个小球,其中黑球有两个,编号为1,2;红球有两个,编号为
3,4.从中不放回的依次取出两个球,A表示事件“取出的两球不同色”,B表示事件“第一次取出的是红
球”,C表示事件“取出的两球同色”,则下列说法错误的是( )
A. A与C互斥 B. A与B相互独立 C. D.
8. 已知 的外接圆圆心为O,且 , ,点D是线段BC上一动点,则
的最小值是( )
A. B. C. D.
二、选择题:本题共3小题,每小题6分,共18分。在每小题给出的选项中,有多项符合题
目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.
9. 已知 是虚数单位,下列说法中正确的是( )
A. 若 , 互为共轭复数,则
B. 若复数z满足 ,则复数z对应的点在以点 为圆心,3为半径的圆上
C. 复数 与 分别表示向量 与 ,则表示向量 的复数为
D. 若 是关于x的方程 的一个根,其中p,q为实数,则
10. 设Ox,Oy是平面内相交的两条数轴,其中 ( 且 ), , 分别是与x轴,
y轴正方向同向的单位向量.若平面向量 满足 ,则有序数对 称为向量 在“仿射”坐
标系xOy下的“仿射”坐标,记作 ,下列命题中是真命题的是( )
A. 已知 ,则
B. 已知 , ,则
C. 已知 , ,则
D. 已知 , ,若 ,则
11. 正方体 的棱长为2,点M是四边形 内部及边界上一动点,点P是棱 上
学学科科网网((北北京京))股股份份有有限限公公司司靠近点A的三等分点,下列结论正确的有( )
A.
B. 当直线AM与平面 所成的角为 时,点M的轨迹长度为
C. 若 ,则点M的运动轨迹长度为
D. 直线 被正方体 的外接球所截得的线段的长度为
三、填空题:本题共3小题,每小题5分,共15分.
12. 已知向量 , ,若 ,则 ______.
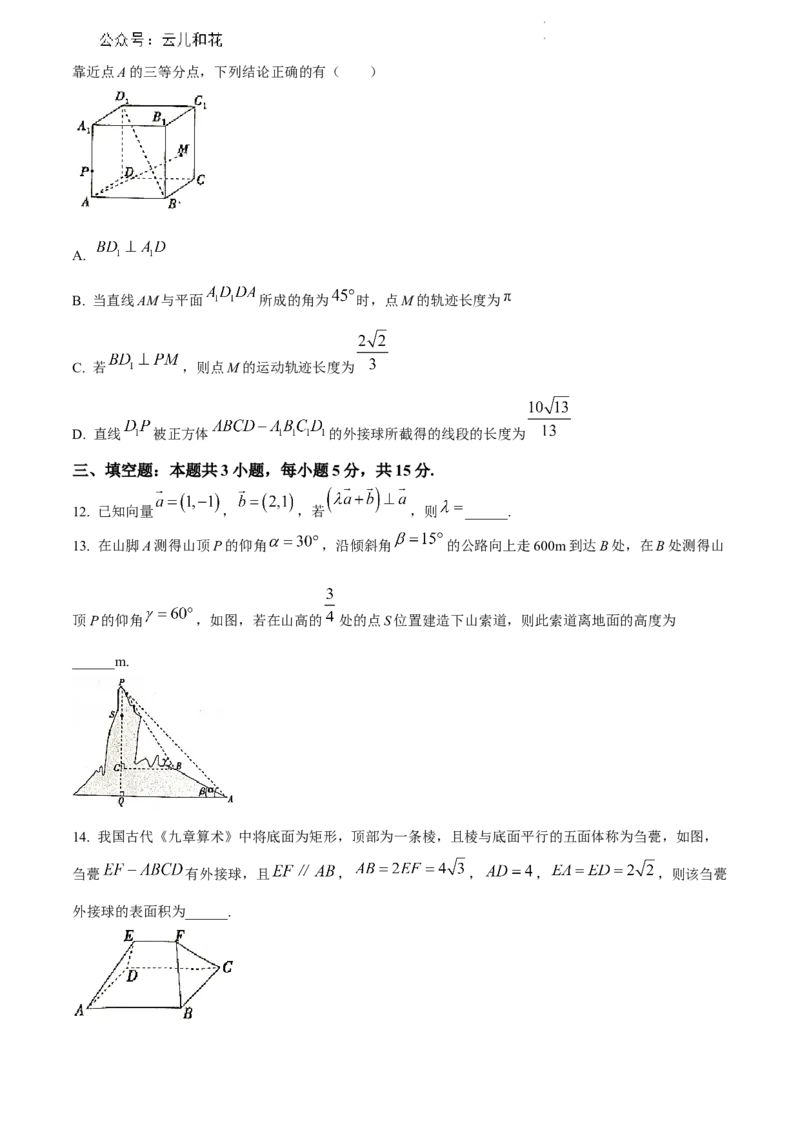
13. 在山脚A测得山顶P的仰角 ,沿倾斜角 的公路向上走600m到达B处,在B处测得山
顶P的仰角 ,如图,若在山高的 处的点S位置建造下山索道,则此索道离地面的高度为
______m.
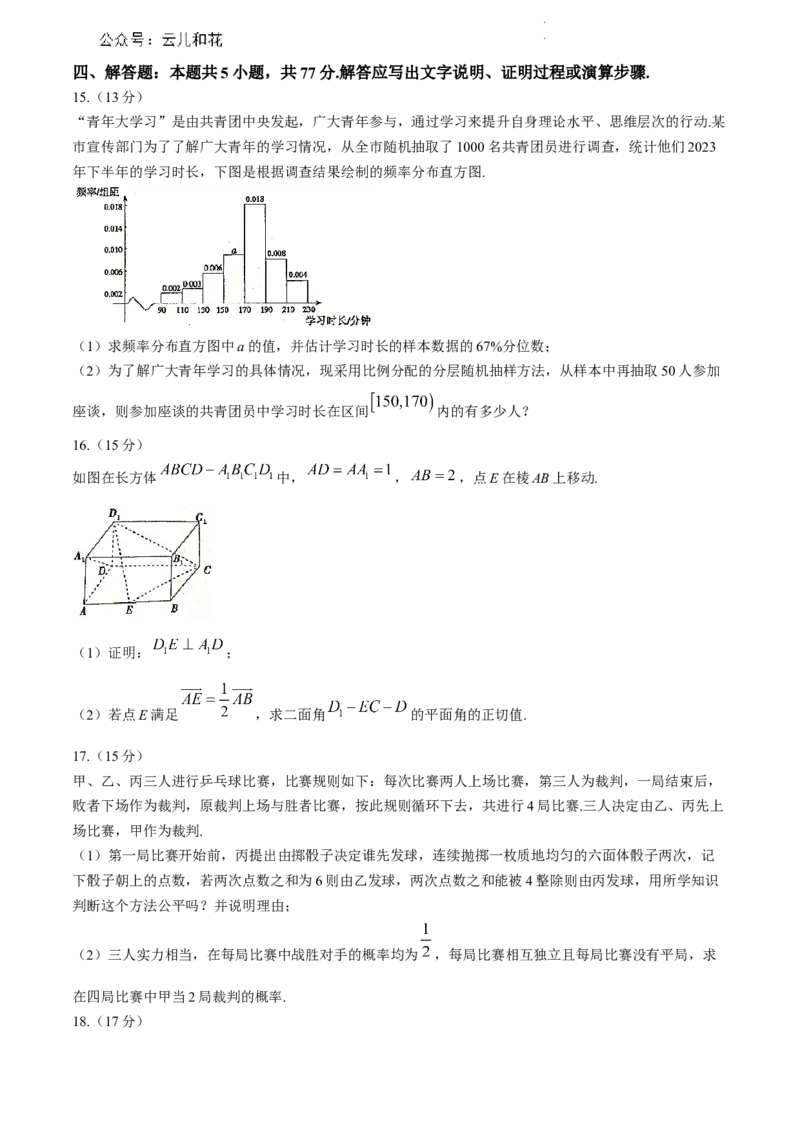
14. 我国古代《九章算术》中将底面为矩形,顶部为一条棱,且棱与底面平行的五面体称为刍甍,如图,
刍甍 有外接球,且 , , , ,则该刍甍
外接球的表面积为______.
学学科科网网((北北京京))股股份份有有限限公公司司四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.
15.(13分)
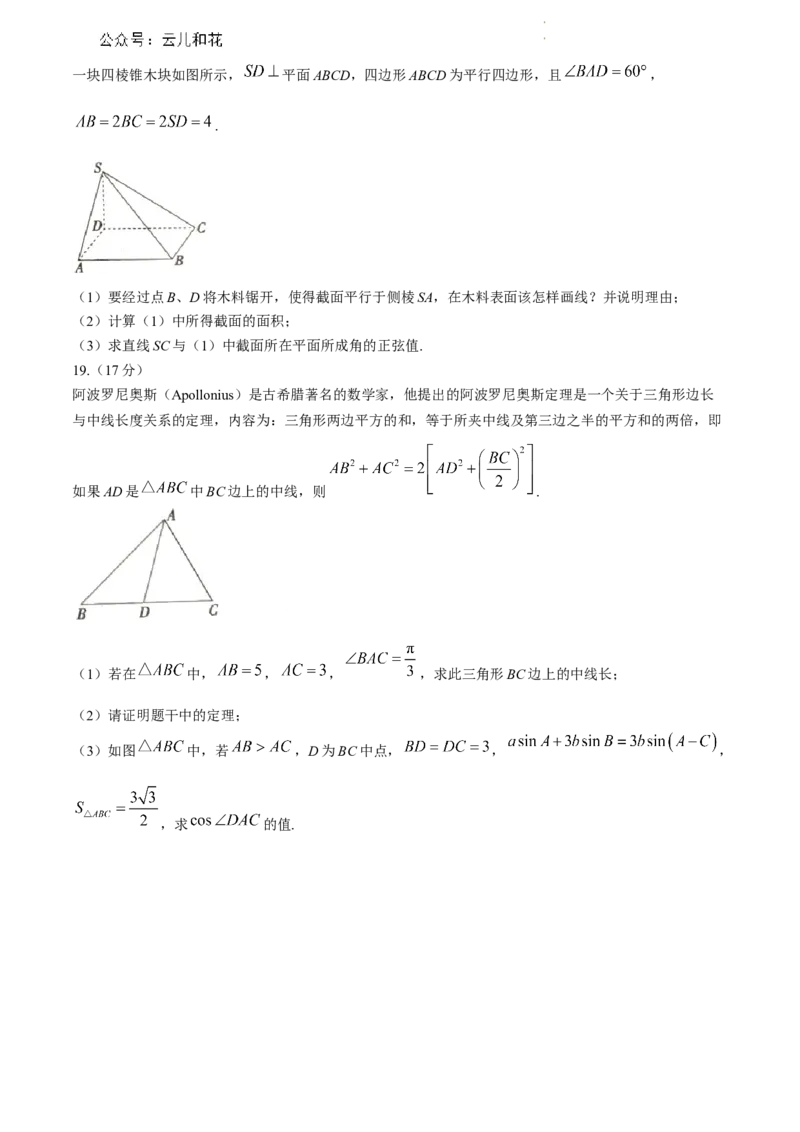
“青年大学习”是由共青团中央发起,广大青年参与,通过学习来提升自身理论水平、思维层次的行动.某
市宣传部门为了了解广大青年的学习情况,从全市随机抽取了1000名共青团员进行调查,统计他们2023
年下半年的学习时长,下图是根据调查结果绘制的频率分布直方图.
(1)求频率分布直方图中a的值,并估计学习时长的样本数据的67%分位数;
(2)为了解广大青年学习的具体情况,现采用比例分配的分层随机抽样方法,从样本中再抽取50人参加
座谈,则参加座谈的共青团员中学习时长在区间 内的有多少人?
16.(15分)
如图在长方体 中, , ,点E在棱AB上移动.
(1)证明: ;
(2)若点E满足 ,求二面角 的平面角的正切值.
17.(15分)
甲、乙、丙三人进行乒乓球比赛,比赛规则如下:每次比赛两人上场比赛,第三人为裁判,一局结束后,
败者下场作为裁判,原裁判上场与胜者比赛,按此规则循环下去,共进行4局比赛.三人决定由乙、丙先上
场比赛,甲作为裁判.
(1)第一局比赛开始前,丙提出由掷骰子决定谁先发球,连续抛掷一枚质地均匀的六面体骰子两次,记
下骰子朝上的点数,若两次点数之和为6则由乙发球,两次点数之和能被4整除则由丙发球,用所学知识
判断这个方法公平吗?并说明理由;
(2)三人实力相当,在每局比赛中战胜对手的概率均为 ,每局比赛相互独立且每局比赛没有平局,求
在四局比赛中甲当2局裁判的概率.
18.(17分)
学学科科网网((北北京京))股股份份有有限限公公司司一块四棱锥木块如图所示, 平面ABCD,四边形ABCD为平行四边形,且 ,
.
(1)要经过点B、D将木料锯开,使得截面平行于侧棱SA,在木料表面该怎样画线?并说明理由;
(2)计算(1)中所得截面的面积;
(3)求直线SC与(1)中截面所在平面所成角的正弦值.
19.(17分)
阿波罗尼奥斯(Apollonius)是古希腊著名的数学家,他提出的阿波罗尼奥斯定理是一个关于三角形边长
与中线长度关系的定理,内容为:三角形两边平方的和,等于所夹中线及第三边之半的平方和的两倍,即
如果AD是 中BC边上的中线,则 .
(1)若在 中, , , ,求此三角形BC边上的中线长;
(2)请证明题干中的定理;
(3)如图 中,若 ,D为BC中点, , ,
,求 的值.
学学科科网网((北北京京))股股份份有有限限公公司司