文档内容
河北省邯郸市2024-2025学年高一下学期期中考试
数学试题
一、单选题
1.已知点 , , ,则 ( )
A. B. C. D.
2.下列结论正确的是( )
A.三个点确定一个平面
B.若空间中两条直线没有公共点,则它们互相平行
C.若一条直线上有无数个点在一个平面内,则这条直线在这个平面内
D.若一条直线上有无数个点在一个平面外,则这条直线与这个平面平行
3.复数 在复平面内对应的点位于( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
4.若 , 均是单位向量,且 ,则 ( )
A. B.3 C.6 D.9
5.如图,这是用斜二测画法画出的水平放置的梯形 的直观图,其中 ,梯
形 的面积为30,则梯形 的高为( )
A. B.10 C. D.20
6.半正多面体,亦称“阿基米德多面体”,是以边数不全相同的正多边形为面的多面体.如图,将正方体
沿交于一顶点的三条棱的中点截去一个三棱锥,如此共截去八个三棱锥,得到一个有十四个面的半正多面
体,这样的半正多面体也称为二十四等边体.由棱长为2的正方体截得的二十四等边体的表面积为( )A. B. C. D.
7. 的内角 的对边分别为 ,已知 , ,则 外接圆的半径
为( )
A. B. C.3 D.6
8.已知复数 , ,若 ,则 的取值范围为
( )
A. B. C. D.
二、多选题
9.已知复数 , ,则( )
A. B. C. D.
10. 的内角 , , 的对边分别为 , , ,若满足 , 的 有两解,则 的值可
能为( )
A.5 B.6 C.7 D.8
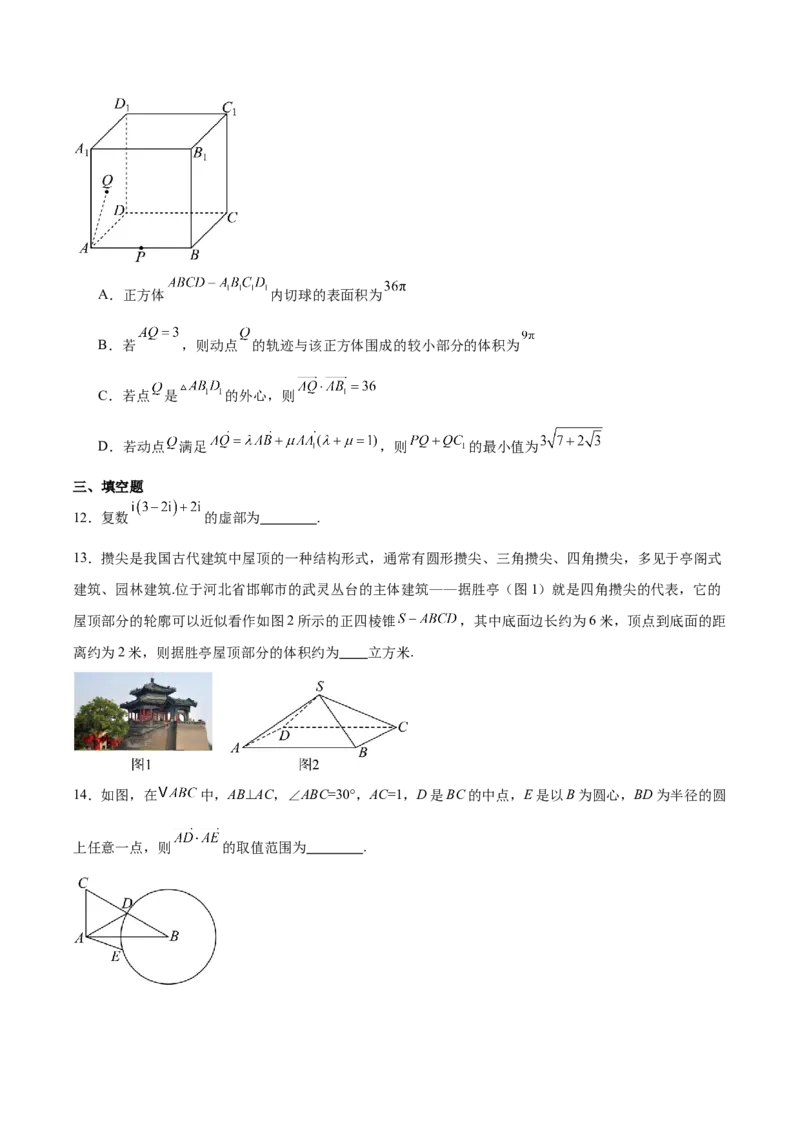
11.如图,正方体 的棱长为6,P是AB的中点, 是正方体 的表面及其
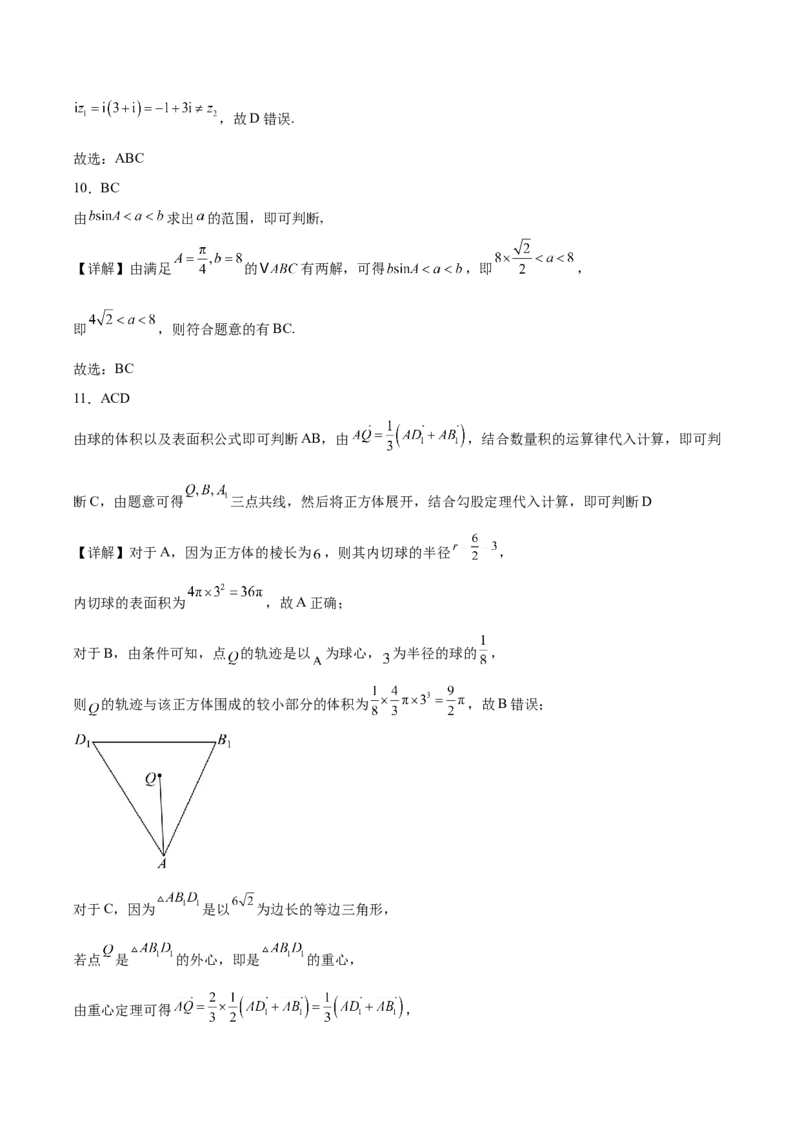
内部一动点,则下列说法正确的是( )A.正方体 内切球的表面积为
B.若 ,则动点 的轨迹与该正方体围成的较小部分的体积为
C.若点 是 的外心,则
D.若动点 满足 ,则 的最小值为
三、填空题
12.复数 的虚部为 .
13.攒尖是我国古代建筑中屋顶的一种结构形式,通常有圆形攒尖、三角攒尖、四角攒尖,多见于亭阁式
建筑、园林建筑.位于河北省邯郸市的武灵丛台的主体建筑——据胜亭(图1)就是四角攒尖的代表,它的
屋顶部分的轮廓可以近似看作如图2所示的正四棱锥 ,其中底面边长约为6米,顶点到底面的距
离约为2米,则据胜亭屋顶部分的体积约为 立方米.
14.如图,在 中,AB⊥AC,∠ABC=30°,AC=1,D是BC的中点,E是以B为圆心,BD为半径的圆
上任意一点,则 的取值范围为 .四、解答题
15.如图,在平行四边形 中, 是 的中点, .
(1)用 , 表示 , ;
(2)若 ,证明: .
16.已知 的内角 , , 的对边分别为 , , ,且 .
(1)求 ;
(2)若 , ,求 的面积.
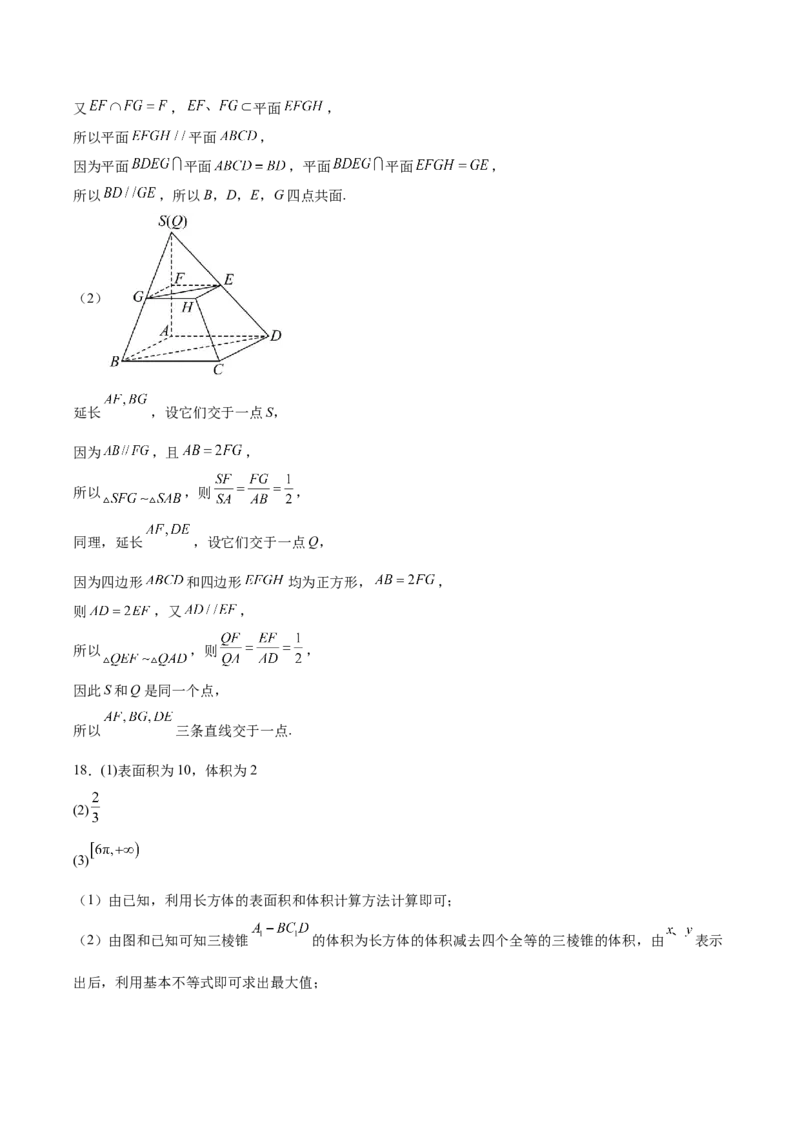
17.如图,在多面体 中,四边形 和四边形 均为正方形,四边形 和四边形
均为梯形,其中 , ,且 .
(1)证明:B,D,E,G四点共面.
(2)证明: 三条直线交于一点.
18.如图,长方体 的长、宽、高分别为x,y,2,且 , .(1)当底面 为正方形时,求长方体 的表面积和体积;
(2)求三棱锥 体积的最大值;
(3)记三棱锥 外接球的表面积为 ,底面ABCD的面积为 ,求 的取值范围.
19.如图,在 中, 是 上一点, 是 上一点,且 .
(1)已知 , 在 的垂直平分线上,且 , .
①求 ;
②若 为 外接圆的圆心, 为 外接圆的圆心,求 .
(2)若 是 的角平分线, ,求 的最大值.题号 1 2 3 4 5 6 7 8 9 10
答案 A C D B C B A D ABC BC
题号 11
答案 ACD
1.A
根据已知点的坐标,得出向量的坐标,求和即可得出答案.
【详解】因为 ,
所以 ,
则 .
故选:A.
2.C
根据空间点、线、面基本定理进行判断.
【详解】三个不共线的点确定一个平面,A错误;
若空间中两条直线没有公共点,则它们互相平行或为异面直线,B错误;
若一条直线上有两个点在一个平面内,则这条直线在这个平面内,C正确;
若一条直线上有无数个点在一个平面外,则这条直线与这个平面平行或与平面相交与一点,D错误.
故选:C
3.D
根据复数代数形式的乘法(乘方)运算化简,再根据复数的几何意义判断即可.
【详解】因为 ,所以 ,
所以 在复平面内对应的点为 ,位于第四象限.
故选:D
4.B
根据数量积的运算律得出 的值,求解即可得出答案.
【详解】由已知可得,
.
所以, .故选:B.
5.C
先求出梯形 的高,再利用平面图与直观图面积的数量关系计算即得.
【详解】因为 ,梯形 的面积为30,
设梯形 的高为 ,则 ,解得 ,
则梯形 的高为 .
故选:C.
6.B
先求出二十四等边体边长为 ,其中有 个面为正方形, 个面为正三角形,
再求其表面积.
【详解】根据题意,正方体截得的二十四等边体边长为 ,
其中有 个面为正方形, 个面为正三角形,
其表面积为 .
故选:B
7.A
根据三角恒等变形得 ,再借助正弦定理角化边可得 ,最后由正弦定理求解.
【详解】根据题意, , ,
即 ,
根据正弦定理,得 ,可得 ,
则 ,所以 ,
则 外接圆的半径为 .
故选:A8.D
根据易知结合复数相等的充要条件化简可得 .进而换元 ,结合二次函数
的性质,即可得出 的最值.
【详解】因为 ,所以 ,
则 ,
所以, .
令 ,
所以, .
根据二次函数的性质可知,当 时, 有最小值 ;
当 时, 有最小值 .
所以, .
故选:D.
9.ABC
A利用复数的模的定义计算;B利用复数的加法运算;C先计算 ,再利用共轭复数的定义;D利用复
数的乘法运算.
【详解】由题意可得, ,则 ,故A正确;
,故B正确;
,则 ,故C正确;,故D错误.
故选:ABC
10.BC
由 求出 的范围,即可判断,
【详解】由满足 的 有两解,可得 ,即 ,
即 ,则符合题意的有BC.
故选:BC
11.ACD
由球的体积以及表面积公式即可判断AB,由 ,结合数量积的运算律代入计算,即可判
断C,由题意可得 三点共线,然后将正方体展开,结合勾股定理代入计算,即可判断D
【详解】对于A,因为正方体的棱长为 ,则其内切球的半径 ,
内切球的表面积为 ,故A正确;
对于B,由条件可知,点 的轨迹是以 为球心, 为半径的球的 ,
则 的轨迹与该正方体围成的较小部分的体积为 ,故B错误;
对于C,因为 是以 为边长的等边三角形,
若点 是 的外心,即是 的重心,
由重心定理可得 ,则
,故C正确;
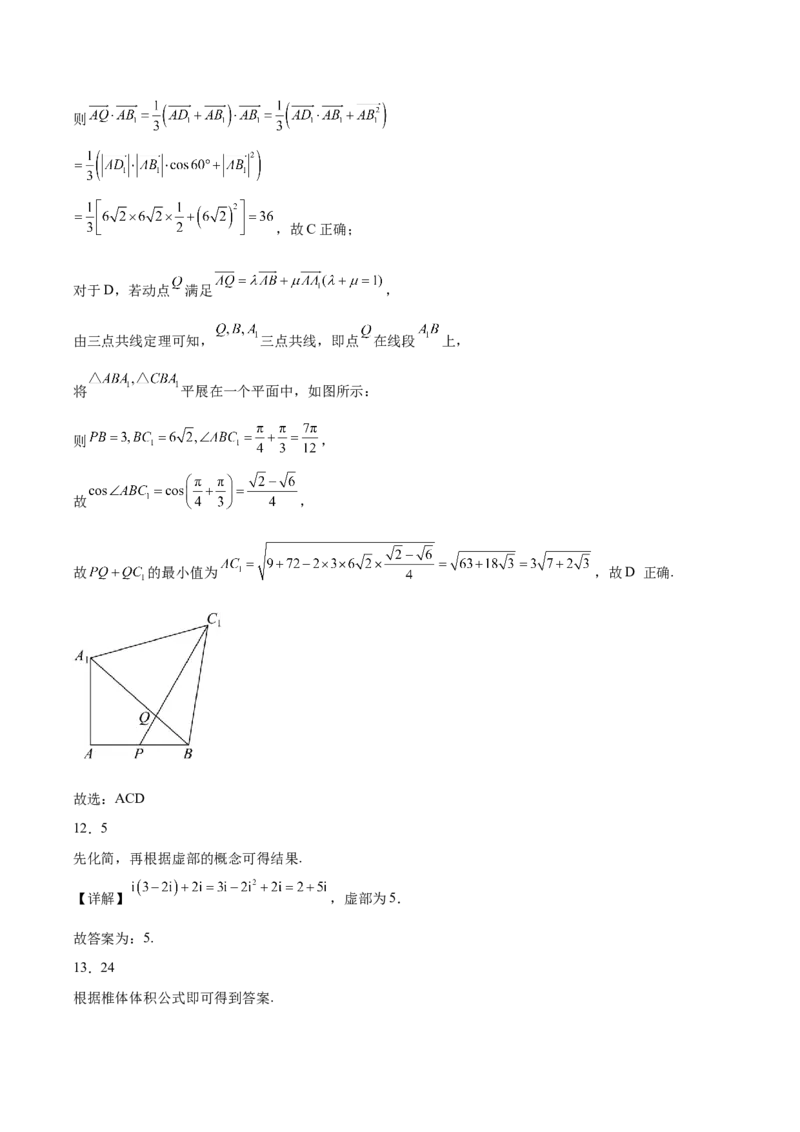
对于D,若动点 满足 ,
由三点共线定理可知, 三点共线,即点 在线段 上,
将 平展在一个平面中,如图所示:
则 ,
故 ,
故 的最小值为 ,故D 正确.
故选:ACD
12.5
先化简,再根据虚部的概念可得结果.
【详解】 ,虚部为5.
故答案为:5.
13.24
根据椎体体积公式即可得到答案.【详解】由题可知,据胜亭屋顶部分的体积约为 立方米.
故答案为:24.
14.
先求出相关线段长,结合图形将 线性表示,利用向量数量积的运算化简成 ,
由 ,根据图形即可判断 的最大、最小值即可.
【详解】因 , ,则 ,
又D是BC的中点,则 ,且 ,
因 ,则
,
由图知,当 与 方向相同时, 取得最大值1;
当 与 方向相反时, 取得最小值 ,
故 的取值范围为 .
故答案为: .
15.(1) ,
(2)证明见解析
(1)根据已知结合图形性质以及向量加法的几何意义,即可得出答案;
(2)根据数量积的运算律,结合已知求出 ,即可得出证明.
【详解】(1)由已知可得, ,则 ,
.
(2)由(1)知, , ,
所以, .
因为 ,
所以 ,
所以, ,
所以, , .
16.(1)
(2)
(1)利用正弦定理将边化角,即可得到 ,再由平方关系解得即可;
(2)由余弦定理求出 ,再由面积公式计算可得.
【详解】(1)因为 ,
由正弦定理得 ,
由 ,得 ,所以 ,即
又 ,解得 或 ,
又 ,所以 ,所以 .
(2)由余弦定理 ,得 ,
解得 或 (负根舍去).
故 的面积为 .
17.(1)证明见解析
(2)证明见解析
(1)由已知可得 平面 , 平面 ,则得平面 平面 ,则由面面平行
的性质可得 ,所以B,D,E,G四点共面;
(2)延长 ,设它们交于一点,由已知可得 ,则 ,同理可得
,则S和Q是同一个点,所以 三条直线交于一点.
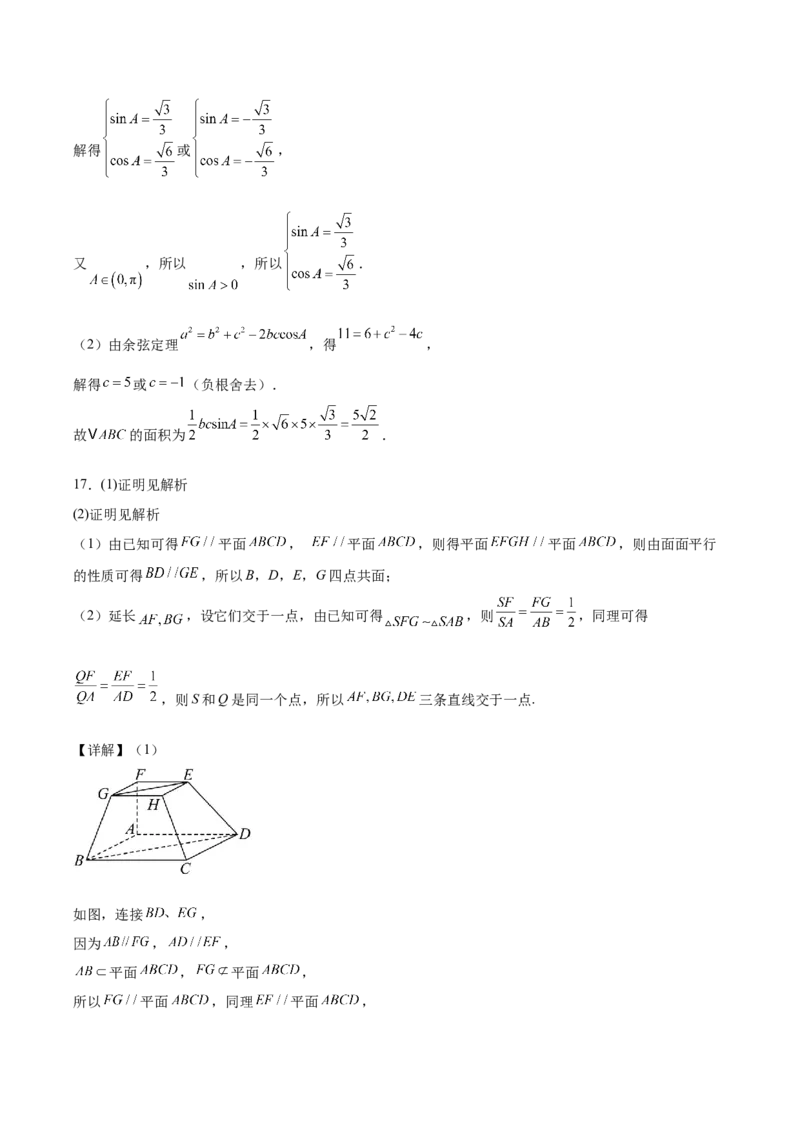
【详解】(1)
如图,连接 ,
因为 , ,
平面 , 平面 ,
所以 平面 ,同理 平面 ,又 , 平面 ,
所以平面 平面 ,
因为平面 平面 ,平面 平面 ,
所以 ,所以B,D,E,G四点共面.
(2)
延长 ,设它们交于一点S,
因为 ,且 ,
所以 ,则 ,
同理,延长 ,设它们交于一点Q,
因为四边形 和四边形 均为正方形, ,
则 ,又 ,
所以 ,则 ,
因此S和Q是同一个点,
所以 三条直线交于一点.
18.(1)表面积为10,体积为2
(2)
(3)
(1)由已知,利用长方体的表面积和体积计算方法计算即可;
(2)由图和已知可知三棱锥 的体积为长方体的体积减去四个全等的三棱锥的体积,由 表示
出后,利用基本不等式即可求出最大值;(3)由题可知,三棱锥 的外接球即长方体 的外接球,则由 表示出 后
代入 并化简,利用基本不等式即可求得 的取值范围.
【详解】(1)因为底面 为正方形,所以 ,
则长方体 的表面积为 ,
体积为 .
(2)由图和已知,
,
当且仅当 时,等号成立,故三棱锥 体积的最大值为 .
(3)由题可知,三棱锥 的外接球即长方体 的外接球,
设该外接球的半径为 则 ,
所以 ,
则 ,
令 ,则 , ,
因为 ,所以 ,
当且仅当 ,即 时,等号成立,所以 的取值范围为 .
19.(1)① ;②1
(2)1
【详解】(1)①因为 , 在 的垂直平分线上,
所以, , ,即 是 的中点,且 为等腰三角形,
所以, , , .
又 ,
所以 , , , .
又 ,
所以 , .
在 中,有 , , ,
由余弦定理可得 ,
所以, .
②易知点 在直线 上,且在直线 的同侧,则 .
设 外接圆的半径为 , 外接圆的半径为 .
则 ,
所以 , .
在 中,有 .
,所以 , .
在 中,有 .
所以, .
(2)由已知 是 的角平分线, , ,
可得, .
所以, ,
即 ,
整理可得 ,
所以有 .
又 ,当且仅当 时等号成立,此时 有最大值,
此时 为等腰三角形, , ,且 ,
此时有 , ,
所以有 .