文档内容
河南省信阳高级中学新校(贤岭校区)、北湖校区
2023-2024 学年高一下期末测试
数学答案
1 2 3 4 5 6
D D A C D D
7 8 9 10 11
A B ACD BCD BD
12.
14.
13.0.88
15.(1)0.035;38.5;47
(2)
【详解】(1) ,
样本平均年龄为 ,
各组的频率依次为 ,
, ,
所以第78百分位数在第4组,设为 ,则 ,
所以第78百分位数为47.
(2)年龄在 的市民人数为 ,年龄在 的市民人数为
,
用分层随机抽样的方法抽取年龄在 的人数为 人,年龄在
的人数为 人,
设年龄在 的4人为 , , , ,年龄在 的2人为 , ,
从这6为市民中抽取两名的基本事件有
,
1
学科网(北京)股份有限公司共15个,
其中2名年龄都在 内的基本事件有 ,共6
个,所以两名幸运市民年龄都在 内的概率为 .
16.(1)证明见解析;
(2) .
【详解】(1)
设CP与ED相交于O,连接OF,
, ,
又 平面DEF, 平面DEF, 平面DEF
(2)设A到平面PCB距离为h,
在梯形 中, ,
,
又 平面 , ,
,
又因为 平面 , 平面 ,所以 ,
则 ;又有 ; ,
所以有 ,即 , ,
而 ,
2
学科网(北京)股份有限公司又F为PA中点,故点F到平面BCP的距离 .
17.(1)
(2)
【详解】(1)因为 ,
所以 ,
所以 ,即 ,
所以 ,
因为 ,所以 ;
(2)因为 ABC的外接圆的面积为 ,所以 ABC的外接圆半径为 ,
△ △
由正弦定理得 , ,
因为 ,所以由正弦定理得 ,
由(1)知 ,
所以 ,得 ,则 ,
所以 ABC的面积为 .
△
18.(1) ;
(2) ;
3
学科网(北京)股份有限公司(3)
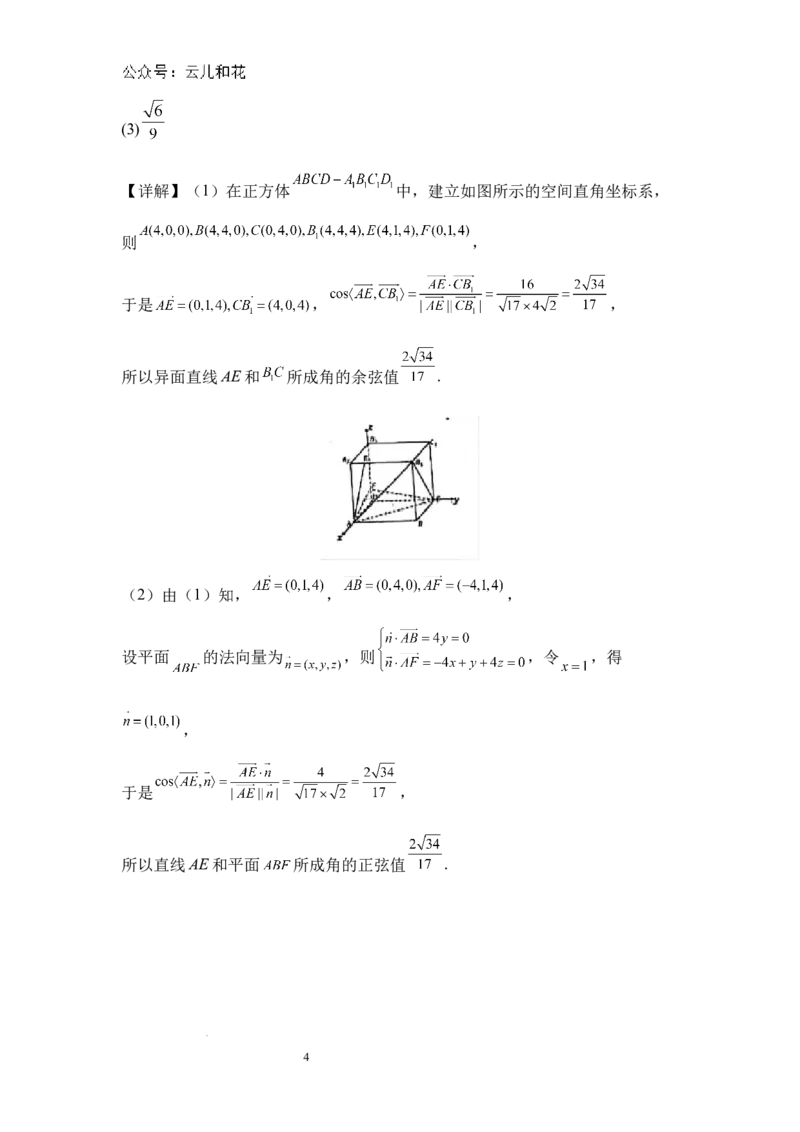
【详解】(1)在正方体 中,建立如图所示的空间直角坐标系,
则 ,
于是 , ,
所以异面直线AE和 所成角的余弦值 .
(2)由(1)知, , ,
设平面 的法向量为 ,则 ,令 ,得
,
于是 ,
所以直线AE和平面 所成角的正弦值 .
4
学科网(北京)股份有限公司19.(1)
(2)① ;②存在, ,
【详解】(1)因为 ,所以由正弦定理可得 ,
所以 ,
所以 ,所以 ,
因为 , ,
所以 或 或 ,
即 或 (舍去)或 (舍去),又 ,所以 ;
(2)①因为 ,所以 ,又 , ,所以 , .
如图,设 , ,
则在 中,由正弦定理,得 ,
5
学科网(北京)股份有限公司所以
在 中,由正弦定理,得 ,所以 ,
,
因为 ,所以 ,
故当 ,即 时, ;
②假设存在实常数 ,k,对于所有满足题意的 , ,都有
成立,
则存在实常数 ,k,对于所有满足题意的 , ,
都有 ,
由题意, 是定值,所以 , 是定值,
对于所有满足题意的 , 成立,
故有 ,
因为 ,从而 ,即 ,
因为 , 为 的内角,所以 ,从而 , .
6
学科网(北京)股份有限公司