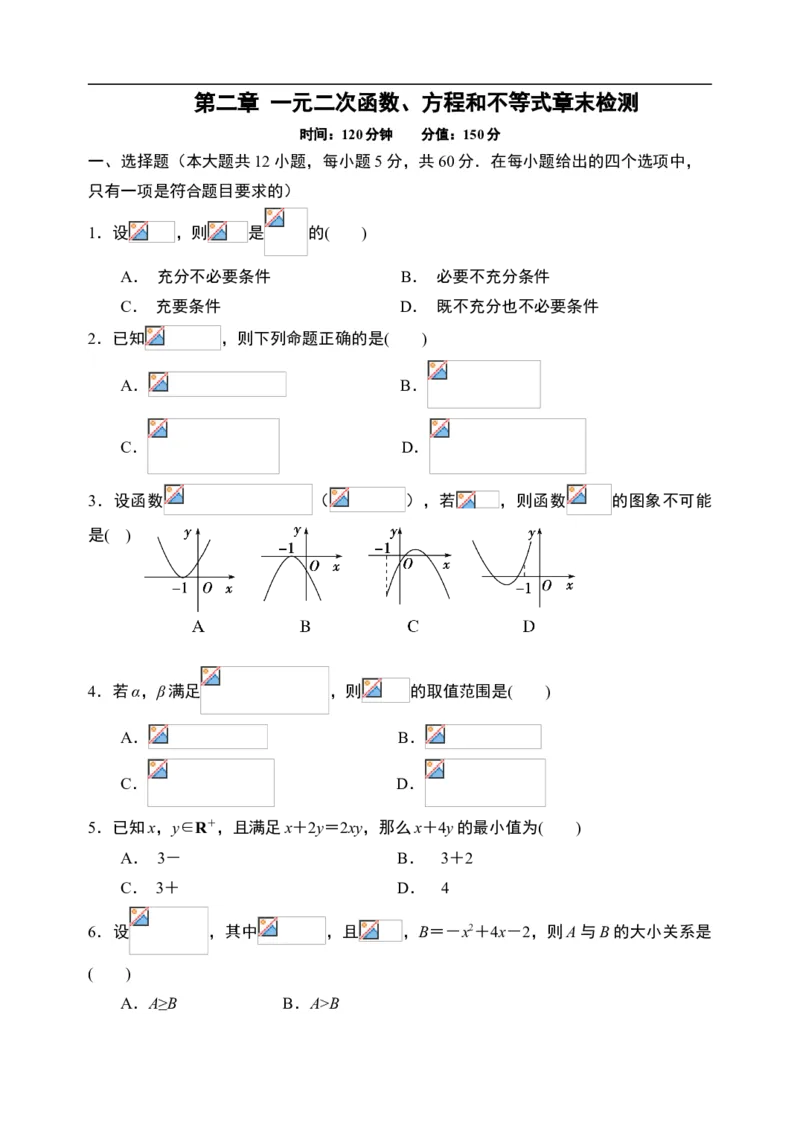
文档内容
第二章 一元二次函数、方程和不等式章末检测
时间:120分钟 分值:150分
一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,
只有一项是符合题目要求的)
1.设 ,则 是 的( )
A. 充分不必要条件 B. 必要不充分条件
C. 充要条件 D. 既不充分也不必要条件
2.已知 ,则下列命题正确的是( )
A. B.
C. D.
3.设函数 ( ),若 ,则函数 的图象不可能
是( )
4.若α,β满足 ,则 的取值范围是( )
A. B.
C. D.
5.已知x,y∈R+,且满足x+2y=2xy,那么x+4y的最小值为( )
A. 3- B. 3+2
C. 3+ D. 4
6.设 ,其中 ,且 ,B=-x2+4x-2,则A与B的大小关系是
( )
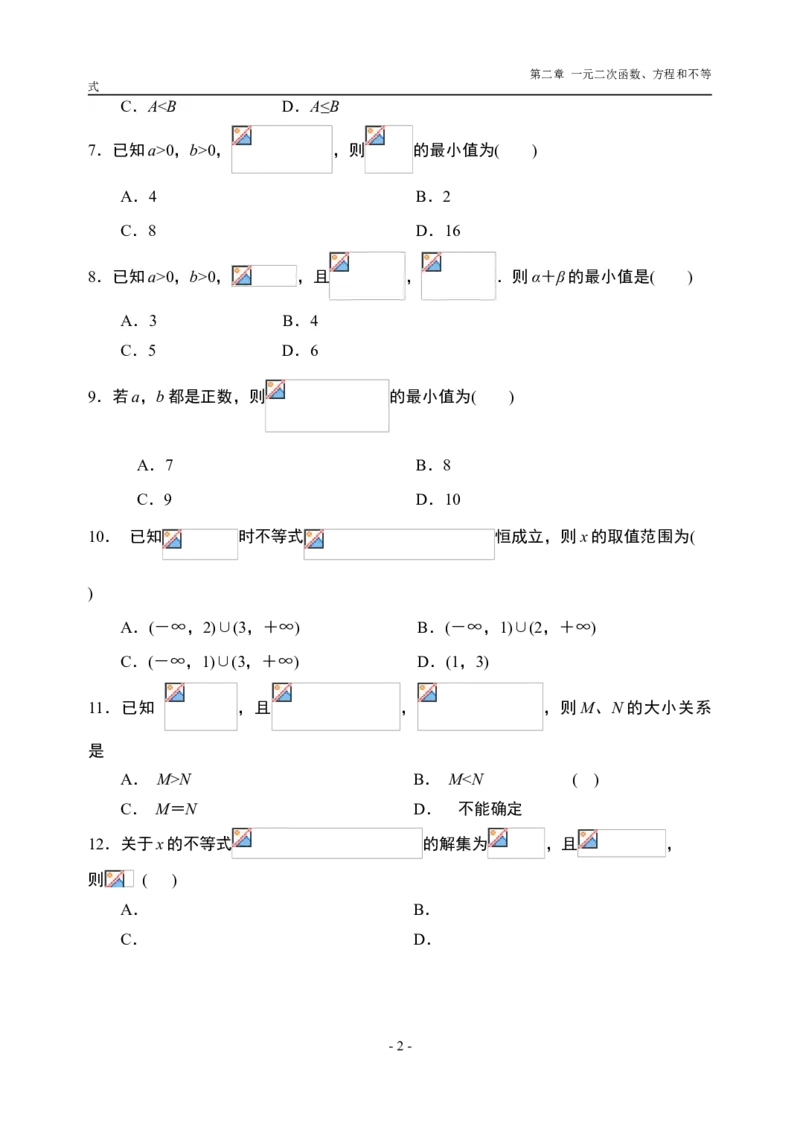
A.A≥B B.A>B第二章 一元二次函数、方程和不等
式
C.A0,b>0, ,则 的最小值为( )
A.4 B.2
C.8 D.16
8.已知a>0,b>0, ,且 , .则α+β的最小值是( )
A.3 B.4
C.5 D.6
9.若a,b都是正数,则 的最小值为( )
A.7 B.8
C.9 D.10
10. 已知 时不等式 恒成立,则x的取值范围为(
)
A.(-∞,2)∪(3,+∞) B.(-∞,1)∪(2,+∞)
C.(-∞,1)∪(3,+∞) D.(1,3)
11.已知 ,且 , ,则M、N的大小关系
是
A. M>N B. M0的解集是{x|-30;
(2)b为何值时,ax2+bx+3≥0的解集为R.
20 . ( 本 小 题 12 分 ) 设 , 且 , 证 明 :
21.(本小题12分)解关于x的不等式 .
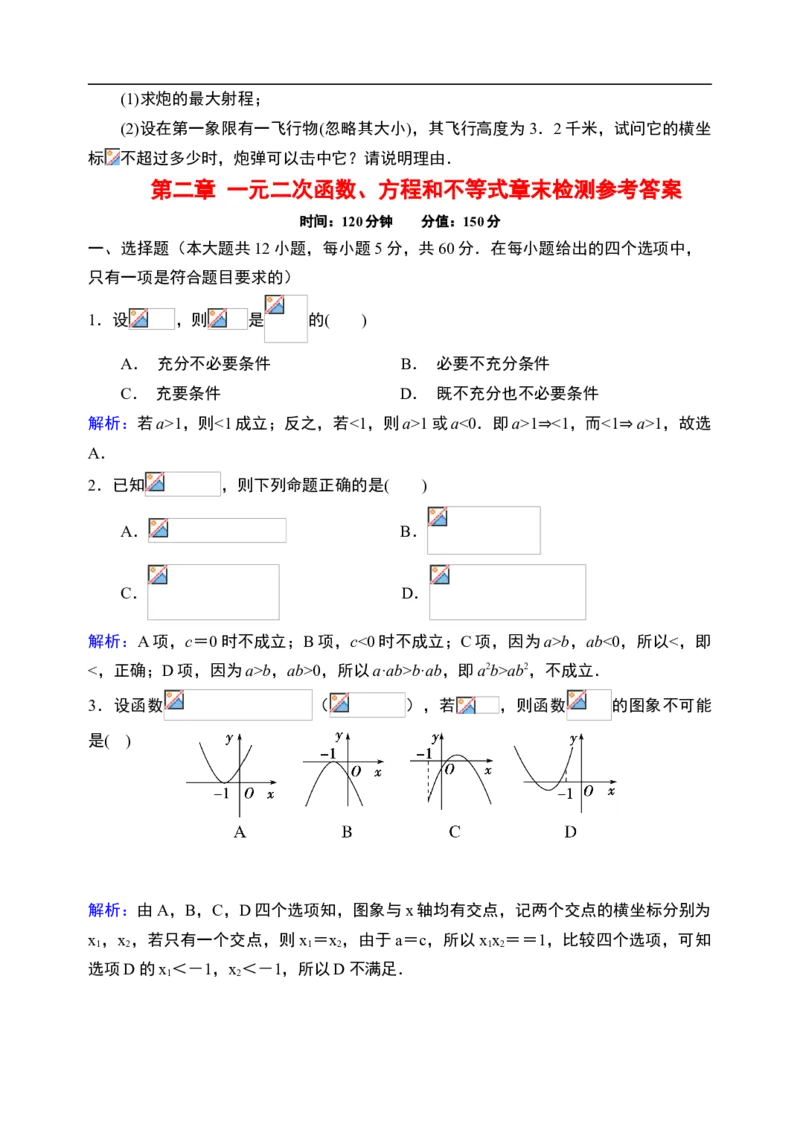
22.(本小题12分)
如图,建立平面直角坐标系 , 轴在地平面上, 轴垂直于地平面,单位长度为1
千 米 . 某 炮 位 于 坐 标 原 点 . 已 知 炮 弹 发 射 后 的 轨 迹 在 方 程
表示的曲线上,其中 与发射方向有关.炮的射程是指
炮弹落地点的横坐标.
- 4 -(1)求炮的最大射程;
(2)设在第一象限有一飞行物(忽略其大小),其飞行高度为3.2千米,试问它的横坐
标 不超过多少时,炮弹可以击中它?请说明理由.
第二章 一元二次函数、方程和不等式章末检测参考答案
时间:120分钟 分值:150分
一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,
只有一项是符合题目要求的)
1.设 ,则 是 的( )
A. 充分不必要条件 B. 必要不充分条件
C. 充要条件 D. 既不充分也不必要条件
解析:若a>1,则<1成立;反之,若<1,则a>1或a<0.即a>1 <1,而<1 a>1,故选
A.
⇒ ⇒
2.已知 ,则下列命题正确的是( )
A. B.
C. D.
解析:A项,c=0时不成立;B项,c<0时不成立;C项,因为a>b,ab<0,所以<,即
<,正确;D项,因为a>b,ab>0,所以a·ab>b·ab,即a2b>ab2,不成立.
3.设函数 ( ),若 ,则函数 的图象不可能
是( )
解析:由A,B,C,D四个选项知,图象与x轴均有交点,记两个交点的横坐标分别为
x ,x ,若只有一个交点,则x =x ,由于a=c,所以xx ==1,比较四个选项,可知
1 2 1 2 1 2
选项D的x<-1,x<-1,所以D不满足.
1 2第二章 一元二次函数、方程和不等
式
4.若α,β满足 ,则 的取值范围是( )
A. B.
C. D.
解析:从题中-<α<β<可分离出三个不等式:-<α< ①,-<β< ②,α<β ③.根据
不等式的性质,②式同乘以-1得-<-β< ④,根据同向不等式的可加性,可得-π<α
-β<π.由③式得α-β<0,所以-π<α-β<0.
5.已知x,y∈R+,且满足x+2y=2xy,那么x+4y的最小值为( )
A. 3- B. 3+2
C. 3+ D. 4
解析:由x>0,y>0,x+2y=2xy,得+=1,则x+4y=(x+4y)·=+1+2+≥3+2=3+
2,当且仅当=时等号成立.
6.设 ,其中a、b是正实数,且a≠b,B=-x2+4x-2,则A与B的大小关系
是( )
A.A≥B B.A>B
C.A2=2,即A>2,
B=-x2+4x-2=-(x2-4x+4)+2=-(x-2)2+2≤2,
即B≤2,所以A>B.
7.已知a>0,b>0, ,则 的最小值为( )
A.4 B.2
C.8 D.16
解析:由a>0,b>0,a+b=+=,得ab=1,
则+≥2=2.当且仅当=,即a=,b=时等号成立.
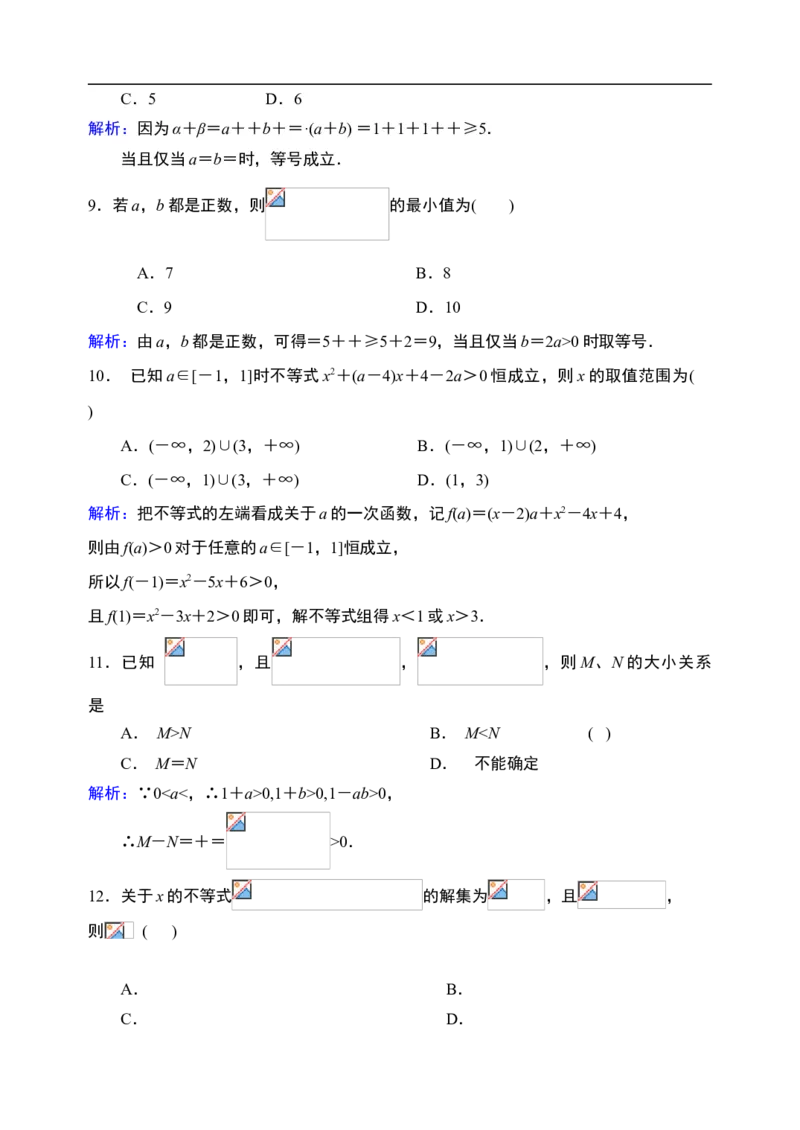
8.已知a>0,b>0, ,且 , .则α+β的最小值是( )
A.3 B.4
- 6 -C.5 D.6
解析:因为α+β=a++b+=·(a+b) =1+1+1++≥5.
当且仅当a=b=时,等号成立.
9.若a,b都是正数,则 的最小值为( )
A.7 B.8
C.9 D.10
解析:由a,b都是正数,可得=5++≥5+2=9,当且仅当b=2a>0时取等号.
10. 已知a∈[-1,1]时不等式x2+(a-4)x+4-2a>0恒成立,则x的取值范围为(
)
A.(-∞,2)∪(3,+∞) B.(-∞,1)∪(2,+∞)
C.(-∞,1)∪(3,+∞) D.(1,3)
解析:把不等式的左端看成关于a的一次函数,记f(a)=(x-2)a+x2-4x+4,
则由f(a)>0对于任意的a∈[-1,1]恒成立,
所以f(-1)=x2-5x+6>0,
且f(1)=x2-3x+2>0即可,解不等式组得x<1或x>3.
11.已知 ,且 , ,则M、N的大小关系
是
A. M>N B. M0,1+b>0,1-ab>0,
∴M-N=+= >0.
12.关于x的不等式 的解集为 ,且 ,
则 ( )
A. B.
C. D.第二章 一元二次函数、方程和不等
式
解析:由条件知x ,x 为方程x2-2ax-8a2=0的两根,则x +x =2a,xx =-8a2,故
1 2 1 2 1 2
(x-x)2=(x+x)2-4xx=(2a)2-4×(-8a2)=36a2=152,得a=.
2 1 1 2 1 2
二、填空题(本大题共4小题,每小题5分,共20分.请把正确答案填在题中横线上)
13.已知x≥0,y≥0,且x+y=1,则x2+y2的取值范围是________.
解析:x2+y2≥=.当且仅当x=y时等号成立.
当x=0或x=1时,x2+y2取最大值,为1.
所以x2+y2的取值范围是.
13.若关于x的方程x2+ax+a2-1=0有一正根和一负根,则a的取值范围为________.
解析:由题意可知,Δ>0且xx=a2-1<0,故-10 (3x+1)(2x-1)>0 x∈∪,
⇒ ⇒
所以原不等式组的解集为x∈∪.
⇒ ⇒
18.(本小题12分)正数x,y满足 .
(1)求xy的最小值;
(2)求x+2y的最小值.
解析:(1)由1=+≥2得xy≥36,当且仅当=,即y=9x=18时取等号,故xy的最小值为
36.
(2)由题意可得x+2y=(x+2y)=19++≥19+2=19+6,当且仅当=,即9x2=2y2
时取等号,故x+2y的最小值为19+6.
19.(本小题12分)若不等式(1-a)x2-4x+6>0的解集是{x|-30;
(2)b为何值时,ax2+bx+3≥0的解集为R.
解析:(1)由题意,知1-a<0且-3和1是方程(1-a)x2-4x+6=0的两根,
所以解得a=3.
所以不等式2x2+(2-a)x-a>0,
即为2x2-x-3>0,
解得x<-1或x>.
所以所求不等式的解集为.
(2)ax2+bx+3≥0,
即为3x2+bx+3≥0,若此不等式解集为R,
则b2-4×3×3≤0,
所以-6≤b≤6.
20 . ( 本 小 题 12 分 ) 设 , 且 , 证 明 :第二章 一元二次函数、方程和不等
式
解析:当abc=1时,++==++,
a+b+c=≥++.
21.(本小题12分)解关于x的不等式 .
解析:原不等式可化为ax2+(a-2)x-2≥0.
①当a=0时,原不等式化为x+1≤0,解得x≤-1.
②当a>0时,原不等式化为(x+1)≥0,
解得x≥或x≤-1.
③当a<0时,原不等式化为(x+1)≤0.
当>-1,即a<-2时,解得-1≤x≤;
当=-1,即a=-2时,解得x=-1满足题意;
当<-1,即-2<a<0,解得≤x≤-1.
综上所述,当a=0时,不等式的解集为{x|x≤-1};
当a>0时,不等式的解集为;
当-2<a<0时,不等式的解集为;
当a=-2时,不等式的解集为{-1};
当a<-2时,不等式的解集为.
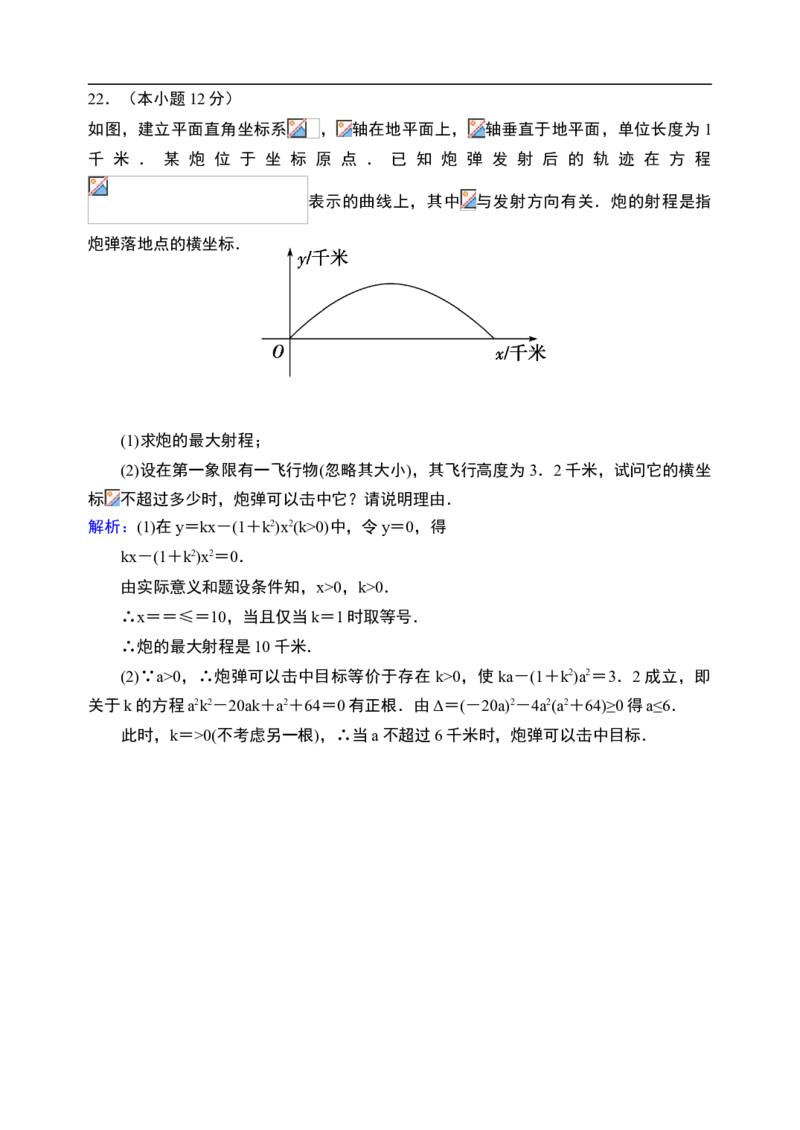
- 10 -22.(本小题12分)
如图,建立平面直角坐标系 , 轴在地平面上, 轴垂直于地平面,单位长度为1
千 米 . 某 炮 位 于 坐 标 原 点 . 已 知 炮 弹 发 射 后 的 轨 迹 在 方 程
表示的曲线上,其中 与发射方向有关.炮的射程是指
炮弹落地点的横坐标.
(1)求炮的最大射程;
(2)设在第一象限有一飞行物(忽略其大小),其飞行高度为3.2千米,试问它的横坐
标 不超过多少时,炮弹可以击中它?请说明理由.
解析:(1)在y=kx-(1+k2)x2(k>0)中,令y=0,得
kx-(1+k2)x2=0.
由实际意义和题设条件知,x>0,k>0.
∴x==≤=10,当且仅当k=1时取等号.
∴炮的最大射程是10千米.
(2)∵a>0,∴炮弹可以击中目标等价于存在k>0,使ka-(1+k2)a2=3.2成立,即
关于k的方程a2k2-20ak+a2+64=0有正根.由Δ=(-20a)2-4a2(a2+64)≥0得a≤6.
此时,k=>0(不考虑另一根),∴当a不超过6千米时,炮弹可以击中目标.